- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Элементы топологии
Содержание
- 1. Презентация по математике на тему Элементы топологии
- 2. Введение в топологию топологией является наука изучающая
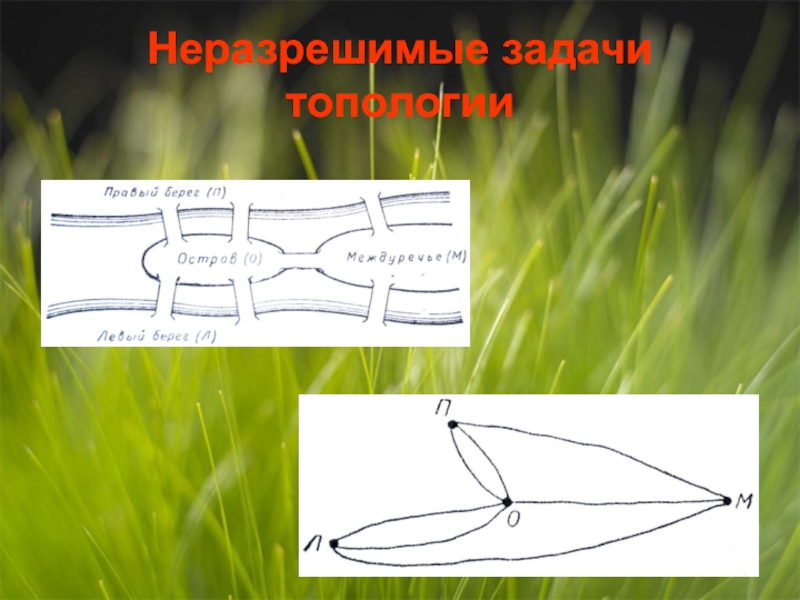
- 3. Неразрешимые задачи топологии
- 4. Неразрешимые задачи топологии
- 5. Топологическое свойство многогранников Если число вершин обозначить
- 6. Проблема четырёх красок Раскрашивая географическую карту, обыкновенно
- 7. Проблема четырёх красокГоловоломка. Вам требуется раскрасить карту
- 8. Решение головоломкиСмешав 1/3 красной краски со всей
Введение в топологию топологией является наука изучающая свойства геометрических фигур, сохраняющихся даже тогда, когда эти фигуры подвергаются таким преобразованиям, которые уничтожают все их и метрические и проективные свойстватопология – это наука, изучающая непрерывность Стартовав как раздел
Слайд 2Введение в топологию
топологией является наука изучающая свойства геометрических фигур, сохраняющихся
даже тогда, когда эти фигуры подвергаются таким преобразованиям, которые уничтожают все их и метрические и проективные свойства
топология – это наука, изучающая непрерывность
Стартовав как раздел геометрии, топология быстро внедрилась и во многие другие области математики. Кажется почти правильным утверждение, что топология представляет собой особое состояние ума и преследует свои собственные цели.
топология – это наука, изучающая непрерывность
Стартовав как раздел геометрии, топология быстро внедрилась и во многие другие области математики. Кажется почти правильным утверждение, что топология представляет собой особое состояние ума и преследует свои собственные цели.
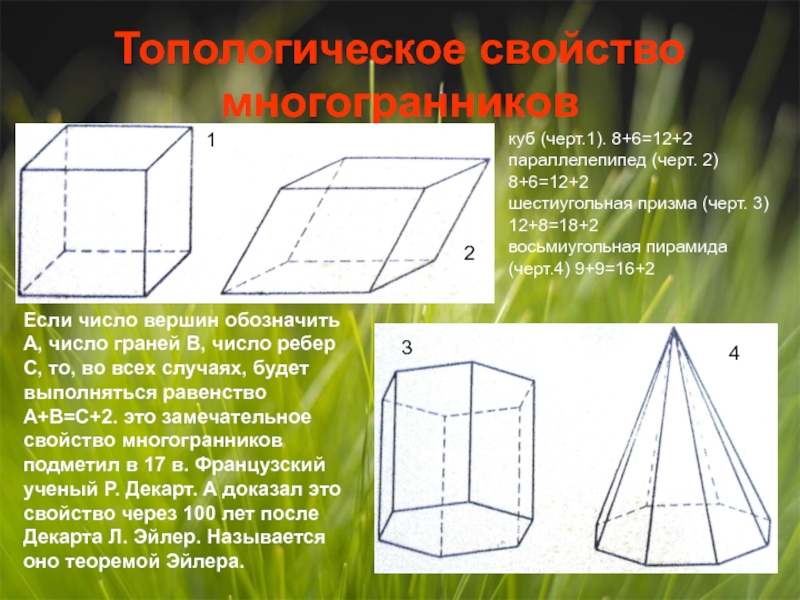
Слайд 5Топологическое свойство многогранников
Если число вершин обозначить А, число граней В,
число ребер С, то, во всех случаях, будет выполняться равенство А+В=С+2. это замечательное свойство многогранников подметил в 17 в. Французский ученый Р. Декарт. А доказал это свойство через 100 лет после Декарта Л. Эйлер. Называется оно теоремой Эйлера.
куб (черт.1). 8+6=12+2 параллелепипед (черт. 2) 8+6=12+2
шестиугольная призма (черт. 3) 12+8=18+2
восьмиугольная пирамида (черт.4) 9+9=16+2
1
2
3
4
Слайд 6Проблема четырёх красок
Раскрашивая географическую карту, обыкновенно стараются распределить цвета, таким
образом, между странами, чтобы две страны, имеющие общую границу, были окрашены по-разному.
К проблеме четырёх красок подступались с разных сторон, из которых по-видимому, наиболее обещающей является формула Эйлера для многогранников, поскольку любую карту можно топологически преобразовать в некоторый многогранник
впервые проблема четырёх красок была поставлена Мёбиусом в 1840г.; позднее её формулировали де Морган в 1850г. и Кэли в 1878г. «Доказательство» её было опубликовано в 1879г. Кемпе, но Хивуд в 1890г. нашёл ошибку в рассуждении Кемпе. Пересматривая доказательство Кемпе, Хивуд обнаружил, что пяти красок всегда достаточно. Несмотря на усилия многих выдающихся математиков, положение вплоть до нашего времени остаётся в сущности неизменным.
К проблеме четырёх красок подступались с разных сторон, из которых по-видимому, наиболее обещающей является формула Эйлера для многогранников, поскольку любую карту можно топологически преобразовать в некоторый многогранник
впервые проблема четырёх красок была поставлена Мёбиусом в 1840г.; позднее её формулировали де Морган в 1850г. и Кэли в 1878г. «Доказательство» её было опубликовано в 1879г. Кемпе, но Хивуд в 1890г. нашёл ошибку в рассуждении Кемпе. Пересматривая доказательство Кемпе, Хивуд обнаружил, что пяти красок всегда достаточно. Несмотря на усилия многих выдающихся математиков, положение вплоть до нашего времени остаётся в сущности неизменным.
Слайд 7Проблема четырёх красок
Головоломка. Вам требуется раскрасить карту ( рис. 10). Площадь
каждой области равна 8м2, за исключением верхней, у которой площадь составляет 16м2. У вас есть следующие краски: КРАСНАЯ, которой хватает ровно, на 24м2; ЖЁЛТАЯ, которой хватает на 24м2; ЗЕЛЁНАЯ, которой хватает на 16м2, и СИНЯЯ, которой хватает на 8м2. Результат должен удовлетворить обычному требованию: соприкасающиеся области нельзя закрашивать в одинаковый цвет.
Слайд 8Решение головоломки
Смешав 1/3 красной краски со всей синей, получим достаточно фиолетовой
краски, чтобы покрасить 16м2. На рис. 11 показана схема раскраски.