- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Элементарные функции и их свойства
Содержание
- 1. Презентация по математике на тему Элементарные функции и их свойства
- 2. Основные свойства функцииОбласть определения функцииОбласть значений функции«Нули»
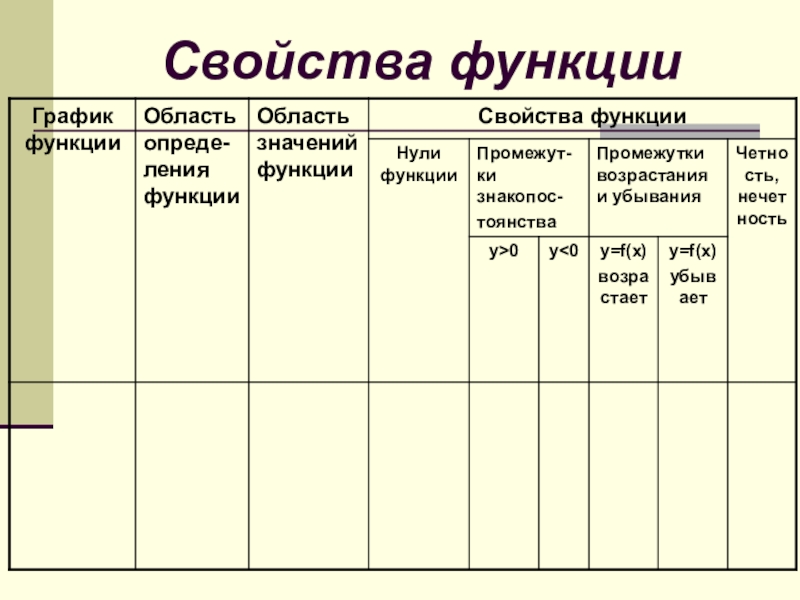
- 3. Свойства функции
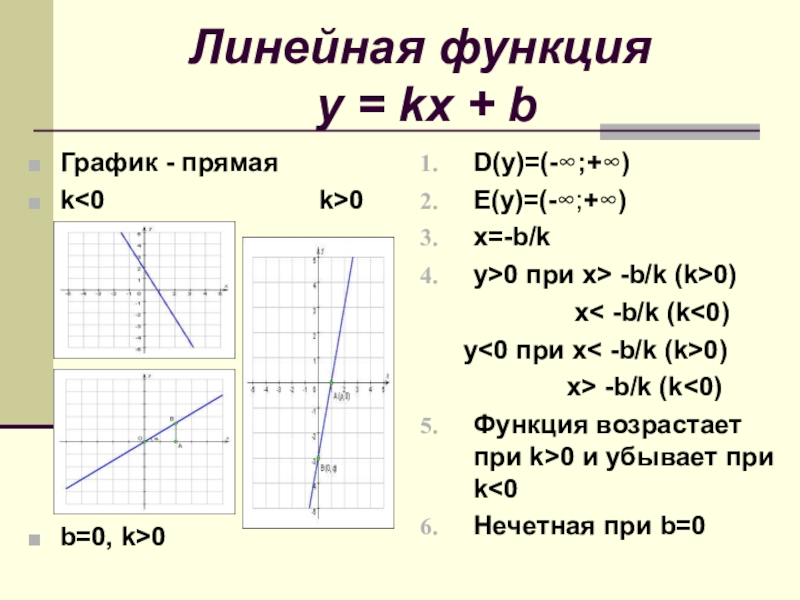
- 4. Линейная функция y = kx +
- 5. Обратная пропорциональность у = k/xГрафик –
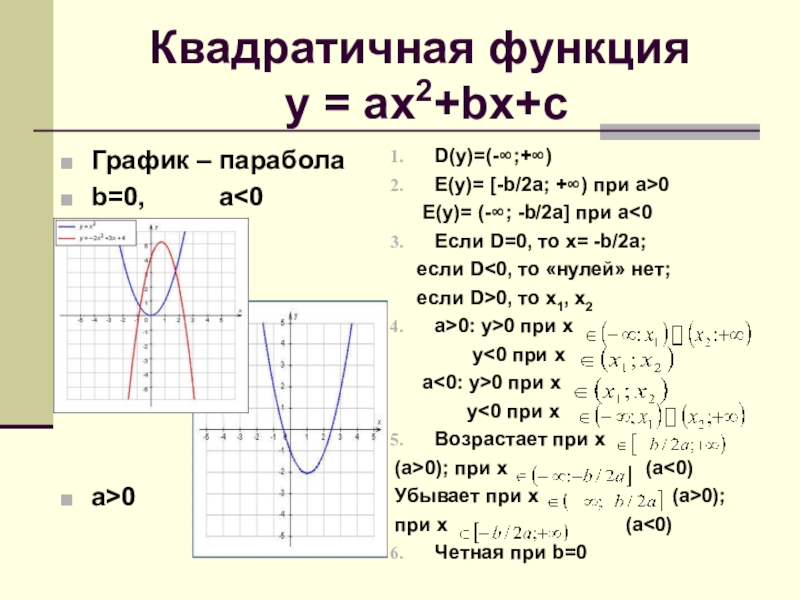
- 6. Квадратичная функция y = ax2+bx+cГрафик –
- 7. Функция y =
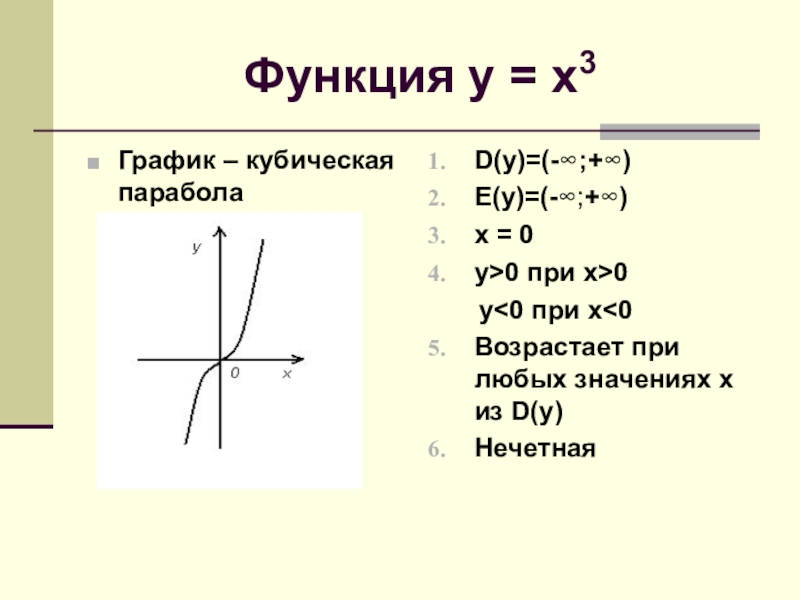
- 8. Функция у = х3График – кубическая параболаD(y)=(-∞;+∞)E(y)=(-∞;+∞)x = 0y>0 при x>0 y
- 9. Степенная функция у = хnn – четноеn
- 10. Красильникова Т.А., учитель математики МБОУ «Школа № 20»г. Рязань
Слайд 2Основные свойства функции
Область определения функции
Область значений функции
«Нули» функции
Промежутки знакопостоянства
Промежутки возрастания и
Четность, нечетность
Ограниченность
Наибольшее и наименьшее значения функции
Выпуклость
Слайд 4Линейная функция
y = kx + b
График - прямая
k
b=0, k>0
D(y)=(-∞;+∞)
E(y)=(-∞;+∞)
x=-b/k
y>0 при x> -b/k (k>0)
x< -b/k (k<0)
y<0 при x< -b/k (k>0)
x> -b/k (k<0)
Функция возрастает при k>0 и убывает при k<0
Нечетная при b=0
Слайд 5Обратная пропорциональность
у = k/x
График – гипербола
k>0
k0
x<0 (k<0)
y<0 при x<0 (k>0)
x>0 (k<0)
Функция возрастает при k<0 и убывает при k>0
Нечетная
Слайд 6Квадратичная функция
y = ax2+bx+c
График – парабола
b=0,
a>0
D(y)=(-∞;+∞)
E(y)= [-b/2a; +∞) при а>0
E(y)= (-∞; -b/2a] при а<0
Если D=0, то х= -b/2a;
если D<0, то «нулей» нет;
если D>0, то х1, х2
а>0: у>0 при х
у<0 при х
а<0: у>0 при х
у<0 при х
Возрастает при х
(а>0); при х (а<0)
Убывает при х (a>0);
при х (а<0)
Четная при b=0
Слайд 7Функция y = Функция у =
D(y)= [0;+∞)
E(y)= [0;+∞)
x = 0
y>0 при x>0
Возрастает при х 0
Ни четная ни нечетная
D(y)=(-∞;+∞)
E(y)= [0;+∞)
x = 0
y>0 при x (- ∞;0)U(0;+∞)
Возрастает при х 0 и убывает при х 0
Четная
Слайд 8Функция у = х3
График – кубическая парабола
D(y)=(-∞;+∞)
E(y)=(-∞;+∞)
x = 0
y>0 при x>0
Возрастает при любых значениях х из D(y)
Нечетная
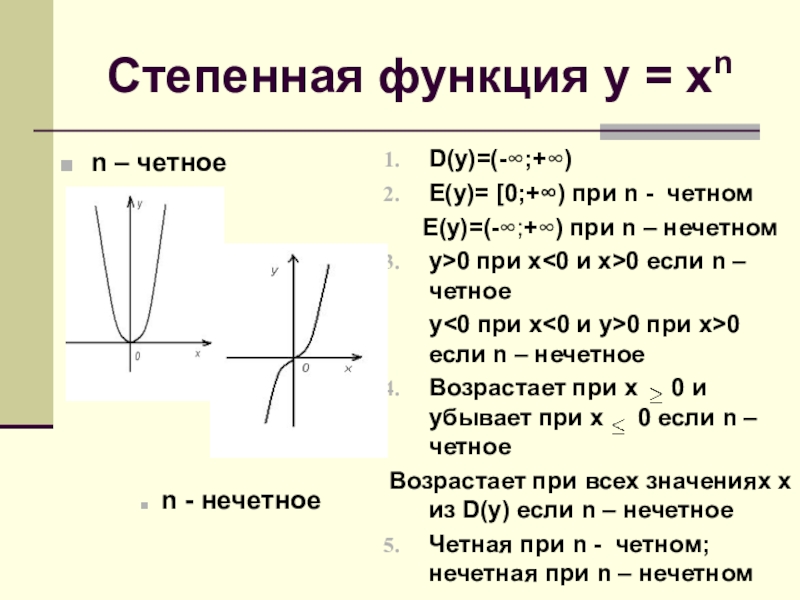
Слайд 9Степенная функция у = хn
n – четное
n - нечетное
D(y)=(-∞;+∞)
E(y)= [0;+∞) при
E(y)=(-∞;+∞) при n – нечетном
у>0 при х<0 и х>0 если n – четное
у<0 при х<0 и у>0 при х>0 если n – нечетное
Возрастает при х 0 и убывает при х 0 если n – четное
Возрастает при всех значениях х из D(y) если n – нечетное
Четная при n - четном; нечетная при n – нечетном