- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Дискретные случайные вличины
Содержание
- 1. Презентация по математике на тему Дискретные случайные вличины
- 2. Дискретная случайная величина (ДСВ)ДСВ – такая величина
- 3. Законом распределения СВ называется соотношение, устанавливающее связь
- 4. 2. Многоугольник распределенияЗакон распределения ДСВPiXix1x2x3x4p1p2p3p4Многоугольник распределенияСумма ординат
- 5. Числовые хар-ки ДСВМатематическое ожидание – сумма произведений
- 6. Числовые хар-ки ДСВСвойства математического ожидания:
- 7. Числовые хар-ки ДСВ2. Дисперсией ДСВХ называется математическое
- 8. Числовые хар-ки ДСВСвойства дисперсии:
- 9. Теоретические моменты ДСВНачальным моментом порядка k СВХ
- 10. Система двух ДСВСистему двух СВ (ХY) можно
- 11. Система двух ДСВТаблица, задающая закон распределения системы двух ДСВ
- 12. Кривая распределения СВХГрафик функции f(x) называется кривой
Дискретная случайная величина (ДСВ)ДСВ – такая величина ,число возможных испытаний которой либо конечно, либо бесконечное множество, но обязательно счетное множество.Например, частота попаданий при 3 выстрелах – Xx1=0, x2=1, x3=2, x4=3ДСВ будет полностью описана с вероятностной точки
Слайд 2Дискретная случайная величина (ДСВ)
ДСВ – такая величина ,число возможных испытаний которой
либо конечно, либо бесконечное множество, но обязательно счетное множество.
Например, частота попаданий при 3 выстрелах – X
x1=0, x2=1, x3=2, x4=3
ДСВ будет полностью описана с вероятностной точки зрения, если будет указано, какую вероятность имеет каждое из событий.
Например, частота попаданий при 3 выстрелах – X
x1=0, x2=1, x3=2, x4=3
ДСВ будет полностью описана с вероятностной точки зрения, если будет указано, какую вероятность имеет каждое из событий.
Слайд 3Законом распределения СВ называется соотношение, устанавливающее связь между возможным значением СВ
и соответствующими вероятностями.
Формы задания закона распределения:
Таблица
Формы задания закона распределения:
Таблица
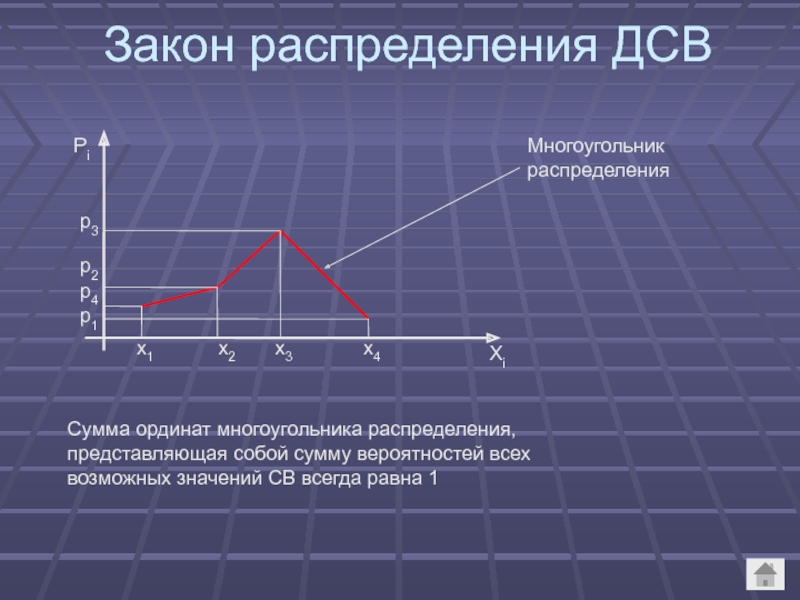
Закон распределения ДСВ
Слайд 42. Многоугольник распределения
Закон распределения ДСВ
Pi
Xi
x1
x2
x3
x4
p1
p2
p3
p4
Многоугольник распределения
Сумма ординат многоугольника распределения, представляющая собой
сумму вероятностей всех возможных значений СВ всегда равна 1
Слайд 5Числовые хар-ки ДСВ
Математическое ожидание – сумма произведений значений СВ на их
вероятности.
Математическое ожидание является хар-кой среднего значения случайной величины
Математическое ожидание является хар-кой среднего значения случайной величины
Слайд 7Числовые хар-ки ДСВ
2. Дисперсией ДСВХ называется математическое ожидание квадрата отклонения случайной
величины от математического ожидания.
Дисперсия характеризует меру рассеяния значений СВ от математического ожидания
При решении задач дисперсию удобно вычислять по формуле:
Дисперсия характеризует меру рассеяния значений СВ от математического ожидания
При решении задач дисперсию удобно вычислять по формуле:
- Среднеквадратичное отклонение
Слайд 9Теоретические моменты ДСВ
Начальным моментом порядка k СВХ называют математическое отношение Хk
Центральным
моментом порядка k СВХ называют математическое ожидание величины
Слайд 10Система двух ДСВ
Систему двух СВ (ХY) можно изображать случайной точкой на
плоскости. Событие, состоящее в попадании случайной точки (ХY) в область D обозначают (X,Y)∩D
Закон распределения системы двух ДСВ можно задать таблицей
Закон распределения системы двух ДСВ можно задать таблицей
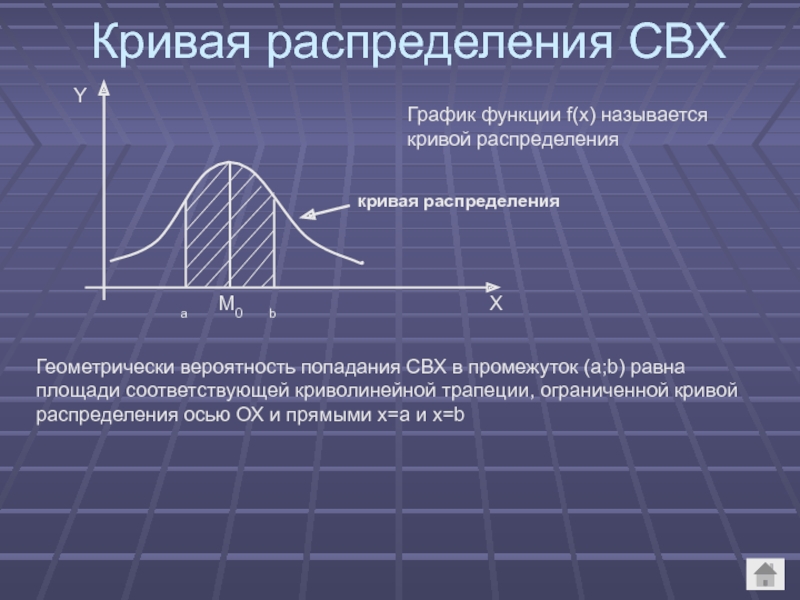
Слайд 12Кривая распределения СВХ
График функции f(x) называется кривой распределения
кривая распределения
Геометрически вероятность попадания
СВХ в промежуток (a;b) равна площади соответствующей криволинейной трапеции, ограниченной кривой распределения осью ОХ и прямыми x=a и x=b