- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Декартова система координат на плоскости (6 класс)
Содержание
- 1. Презентация по математике на тему Декартова система координат на плоскости (6 класс)
- 2. Зададим на плоскости две координатные оси, расположив
- 3. Прямоугольную систему координат хОу называют декартовой системой
- 4. Пусть А – произвольная точка координатной плоскости.
- 5. Координаты точки записывают в скобках рядом с
- 6. Прямоугольная система координат разделяет плоскость на четыре
- 7. Итак, если на плоскости задана прямоугольная система
- 8. Желаю удачи при изучении данной темы
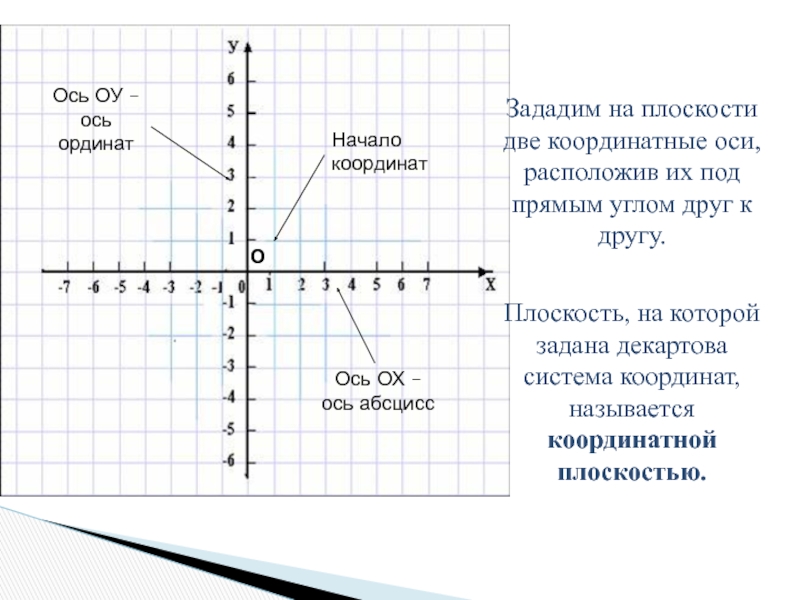
Зададим на плоскости две координатные оси, расположив их под прямым углом друг к другу.Плоскость, на которой задана декартова система координат, называется координатной плоскостью.ОНачало координатОсь ОУ – ось ординатОсь ОХ – ось абсцисс
Слайд 2Зададим на плоскости две координатные оси, расположив их под прямым углом
друг к другу.
Плоскость, на которой задана декартова система координат, называется координатной плоскостью.
Плоскость, на которой задана декартова система координат, называется координатной плоскостью.
О
Начало координат
Ось ОУ – ось ординат
Ось ОХ –
ось абсцисс
Слайд 3Прямоугольную систему координат хОу называют декартовой системой координат по имени французского
математика и философа
Рене Декарта.
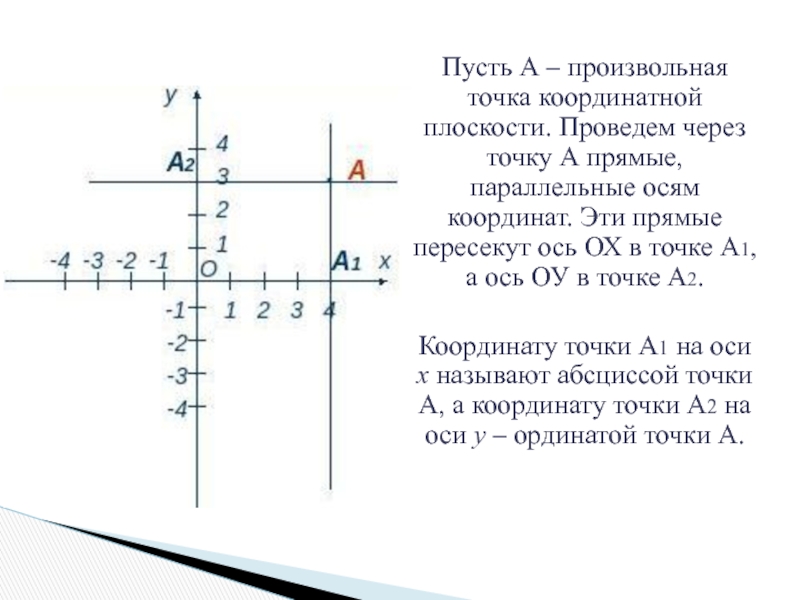
Слайд 4Пусть А – произвольная точка координатной плоскости. Проведем через точку А
прямые, параллельные осям координат. Эти прямые пересекут ось ОХ в точке А1, а ось ОУ в точке А2.
Координату точки А1 на оси х называют абсциссой точки А, а координату точки А2 на оси у – ординатой точки А.
Координату точки А1 на оси х называют абсциссой точки А, а координату точки А2 на оси у – ординатой точки А.
Слайд 5Координаты точки записывают в скобках рядом с буквой А(х; у). Причем
на первом месте записывают абсциссу точки, а на втором – ординату.
А(3;1)
B(2;3)
C(1;2)
D(-2;2)
E(-1;-2)
F(4;-1)
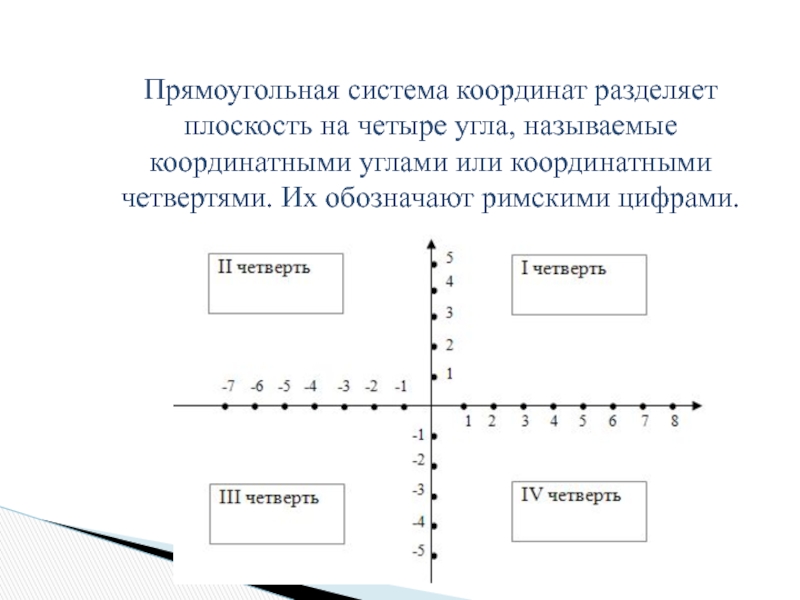
Слайд 6Прямоугольная система координат разделяет плоскость на четыре угла, называемые координатными углами
или координатными четвертями. Их обозначают римскими цифрами.
Слайд 7Итак, если на плоскости задана прямоугольная система координат хОу, то:
Каждой точке
плоскости поставлена в соответствие упорядоченная пара чисел (координаты точки).
Разным точкам плоскости поставлены в соответствие разные упорядоченные пары чисел.
Каждая упорядоченная пара чисел соответствует некоторой одной точке плоскости.
Иначе говоря, между точками плоскости и упорядоченными парами числе установлено взаимно однозначное соответствие.
Разным точкам плоскости поставлены в соответствие разные упорядоченные пары чисел.
Каждая упорядоченная пара чисел соответствует некоторой одной точке плоскости.
Иначе говоря, между точками плоскости и упорядоченными парами числе установлено взаимно однозначное соответствие.