Презентация, доклад по математике на тему: Аксиомы стереометрии

Содержание

1. Презентация по математике на тему: Аксиомы стереометрии
2. Стереометрия – это раздел геометрии, в котором
3. Основные свойства точек, прямых и плоскостей, касающихся их взаимного расположения, выражены в аксиомах.
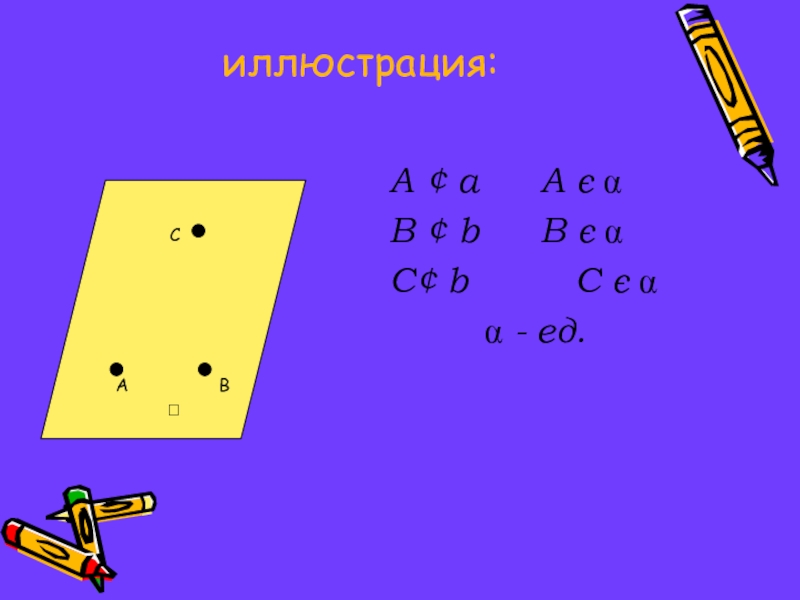
4. А1 Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
5. иллюстрация:А ¢ а А є 
6. А2 Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
7. ИЛЛЮСТРАЦИЯ:А є a
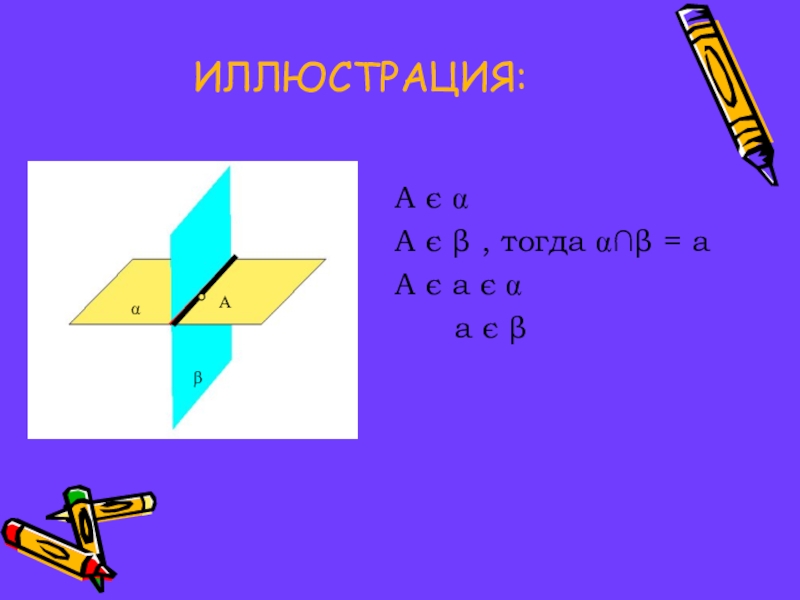
8. А3 Если две плоскости имеют общую точку, то
9. ИЛЛЮСТРАЦИЯ:А є А є β , тогда
10. Некоторые следствия из аксиом Теорема 1: Через прямую
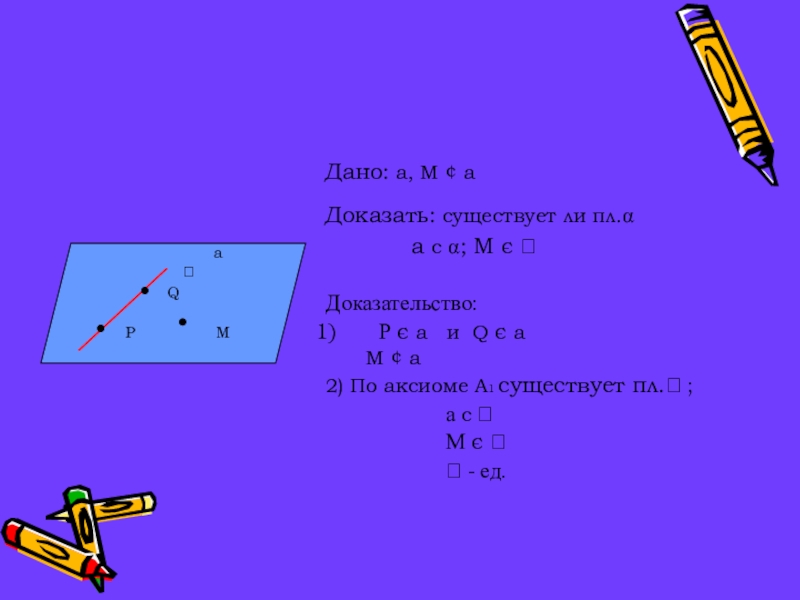
11. Дано: a, М ¢ aДоказать: существует ли
12. Теорема 2: Через две пересекающиеся прямые проходит плоскость, и притом только одна.
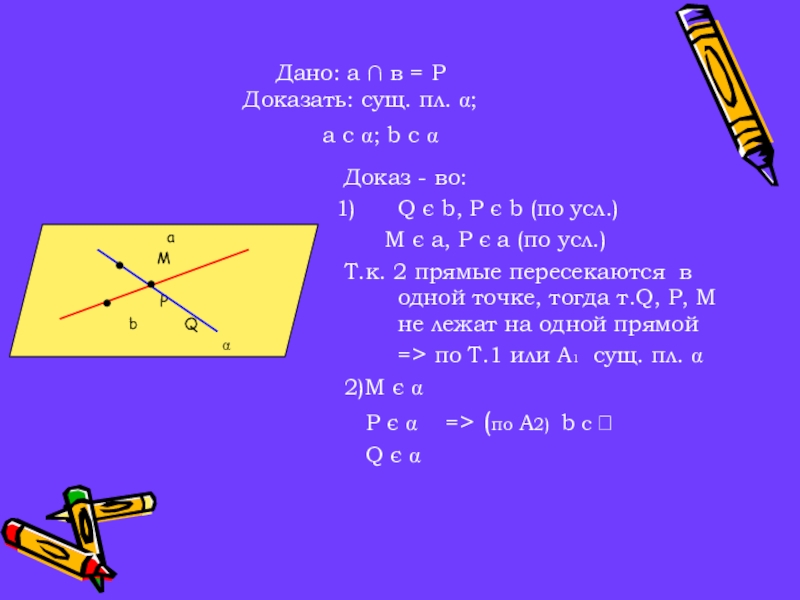
13. Дано: а ∩ в = Р Доказать:
14. 3) Р є а
15. Спасибо за внимание!!!

Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве. Слово «стереометрия» происходит от греч. Слов «стереос»-объемный, пространственный и «метрео»-измерять.

Главная
Математика
Презентация по математике на тему: Аксиомы стереометрии

Слайд 1Проектная работа на тему : «Аксиомы стереометрии»
Руководитель

проекта:
Змаева Е.А. Выполнила: Зейналова Элеонора 11а кл.

Проектная работа на тему : «Аксиомы стереометрии»Руководитель проекта: Змаева Е.А. Выполнила: Зейналова Элеонора

Слайд 2Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в

пространстве. Слово «стереометрия» происходит от греч. Слов «стереос»-объемный, пространственный и «метрео»-измерять.

Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве. Слово «стереометрия» происходит от греч.

Слайд 3Основные свойства точек, прямых и плоскостей, касающихся их взаимного расположения, выражены

в аксиомах.

Слайд 4А1
Через любые три точки, не лежащие на одной прямой, проходит плоскость,

и притом только одна.

Слайд 5иллюстрация:
А ¢ а А є 

В ¢ b В є 
С¢ b С є 
 - ед.

С

А В


Слайд 6А2

Если две точки прямой лежат в плоскости, то все точки прямой

лежат в этой плоскости.

Слайд 7ИЛЛЮСТРАЦИЯ:
А є a А є 

и
В є a В є 
Тогда a є 

а
В

А


Слайд 8А3

Если две плоскости имеют общую точку, то они имеют общую прямую,

на которой лежат все общие точки этих плоскостей.

А3 Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки

Слайд 9ИЛЛЮСТРАЦИЯ:
А є 
А є β , тогда ∩β = a
А є

a є 
a є β



ИЛЛЮСТРАЦИЯ:А є А є β , тогда ∩β = aА є a є  a

Слайд 10Некоторые следствия из аксиом
Теорема 1:

Через прямую и не лежащую на

ней точку проходит плоскость, и притом только одна.

Некоторые следствия из аксиом Теорема 1: Через прямую и не лежащую на ней точку проходит плоскость, и притом

Слайд 11

Дано: a, М ¢ a
Доказать: существует ли пл.
a c

; М є 

Доказательство:
Р є a и Q є a
М ¢ a
2) По аксиоме А1 существует пл. ;
а c 
М є 
 - ед.

a 
Q

P M

Дано: a, М ¢ aДоказать: существует ли пл. a c ; М є Доказательство:Р є a

Слайд 12 Теорема 2:

Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Слайд 13Дано: а ∩ в = Р Доказать: сущ. пл. ; a c

; b c 

Доказ - во:
Q є b, Р є b (по усл.)
М є а, Р є а (по усл.)
Т.к. 2 прямые пересекаются в одной точке, тогда т.Q, P, M не лежат на одной прямой => по Т.1 или А1 сущ. пл. 
2)М є 
Р є  => (по А2) b c 
Q є 

а
М

P
b Q
