- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему 2-3 признаки равенства треугольников
Содержание
- 1. Презентация по математике на тему 2-3 признаки равенства треугольников
- 2. Если сторона и два прилегающих к ней
- 3. АВСВ₁С₁А₁Наложим ∆АВС на ∆А₁В₁С₁,так чтобы вершина А
- 4. Решение задач.АCDBДАНО:∠АСВ=∠ACD,АС-биссектриса ∠ВAD.Доказать: ∆АВС=∆АDСДоказательство:1.АС-общая2. ∠АСВ=∠ACD} по усл.3. ∠1=∠2} по свойствубиссектрисы12Следовательно, ∆АВС=∆АDС ч.т.д.
- 5. 1243АСВОDДано:∠1=∠2; ∠3=∠4.Доказать: ∆АВС=∆DCB; ∆АВО=∆DCO.Доказательство:1.ВС-общая2.∠В=∠С, т.к.∠1+∠3 =∠В;
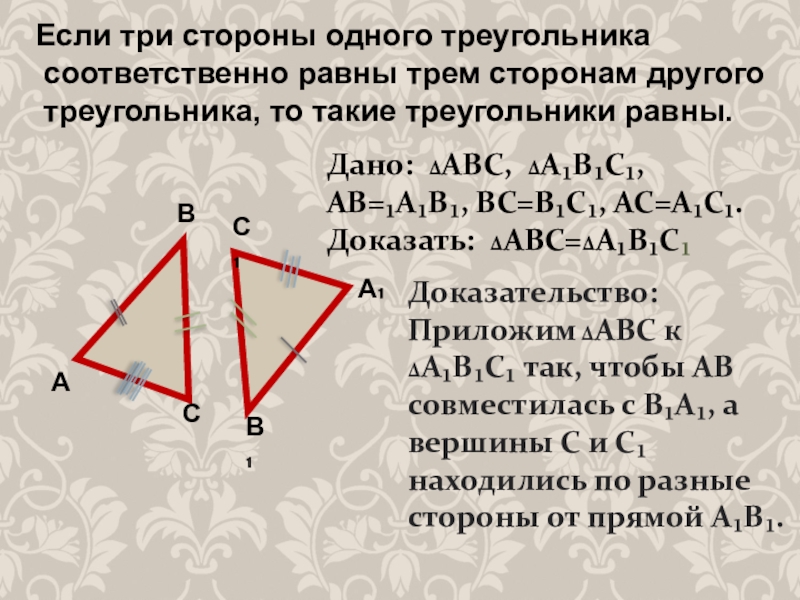
- 6. Если три стороны одного треугольника соответственно равны
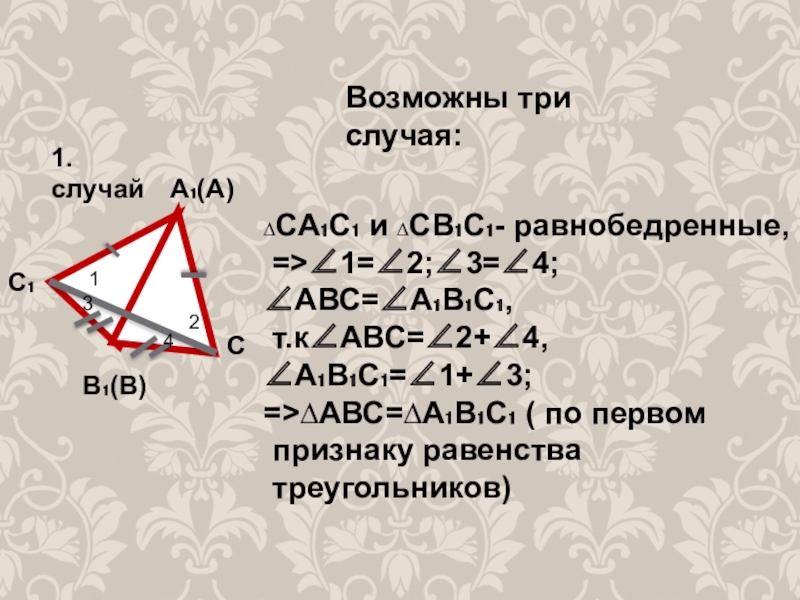
- 7. Возможны три случая:А₁(А)СВ₁(В)С₁∆СА₁С₁ и ∆СВ₁С₁- равнобедренные, =>∠1=∠2;∠3=∠4;
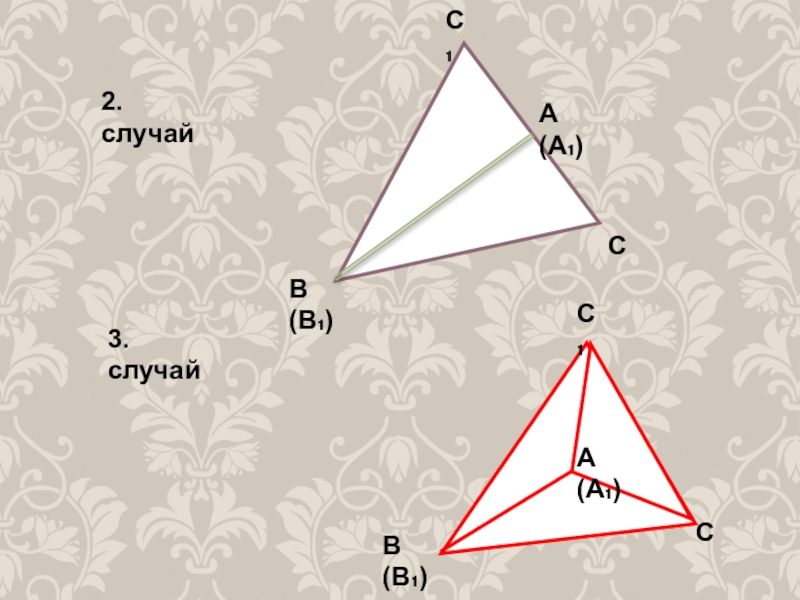
- 8. 2.случайА(А₁)В(В₁)С₁С3.случайА(А₁)С₁СВ(В₁)
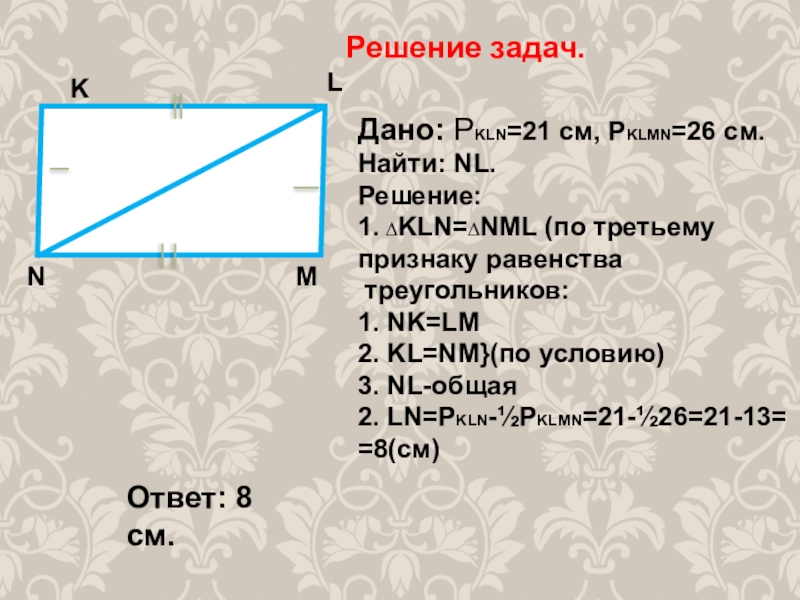
- 9. Решение задач.KMLNДано: РKLN=21 cм, РKLMN=26 см.Найти: NL.Решение:1.
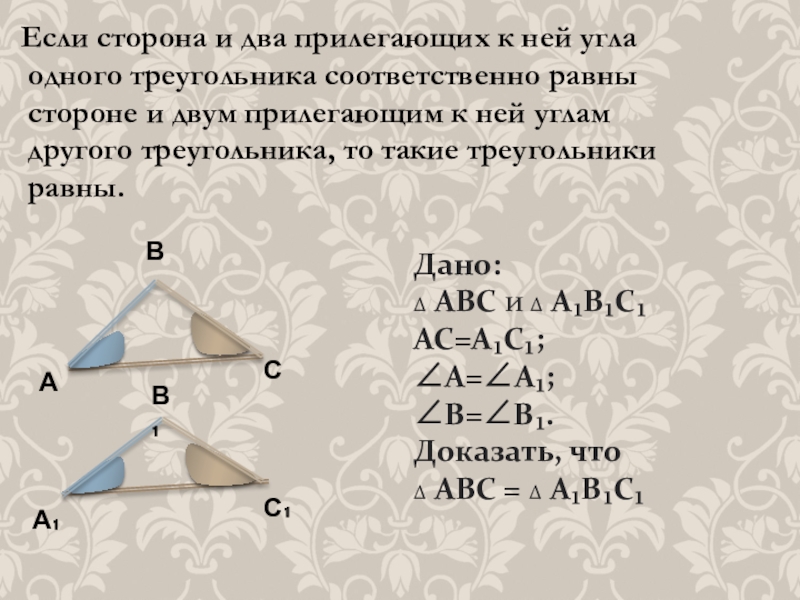
Слайд 2Если сторона и два прилегающих к ней угла
одного треугольника соответственно
стороне и двум прилегающим к ней углам
другого треугольника, то такие треугольники
равны.
Дано:
∆ АВС и ∆ А₁В₁С₁
АС=А₁С₁; ∠А=∠А₁; ∠В=∠В₁.
Доказать, что ∆ АВС = ∆ А₁В₁С₁
А
С
В
С₁
А₁
В₁
Слайд 3
А
В
С
В₁
С₁
А₁
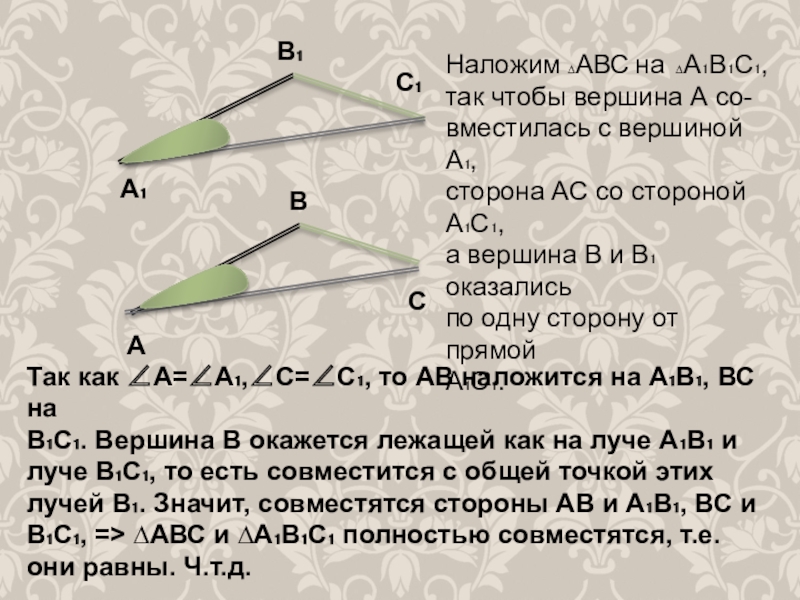
Наложим ∆АВС на ∆А₁В₁С₁,
так чтобы вершина А со-
вместилась с вершиной А₁,
сторона
а вершина В и В₁ оказались
по одну сторону от прямой
А₁С₁.
Так как ∠А=∠А₁,∠С=∠С₁, то АВ наложится на А₁В₁, ВС на
В₁С₁. Вершина В окажется лежащей как на луче А₁В₁ и луче В₁С₁, то есть совместится с общей точкой этих лучей В₁. Значит, совместятся стороны АВ и А₁В₁, ВС и В₁С₁, => ∆АВС и ∆А₁В₁С₁ полностью совместятся, т.е. они равны. Ч.т.д.
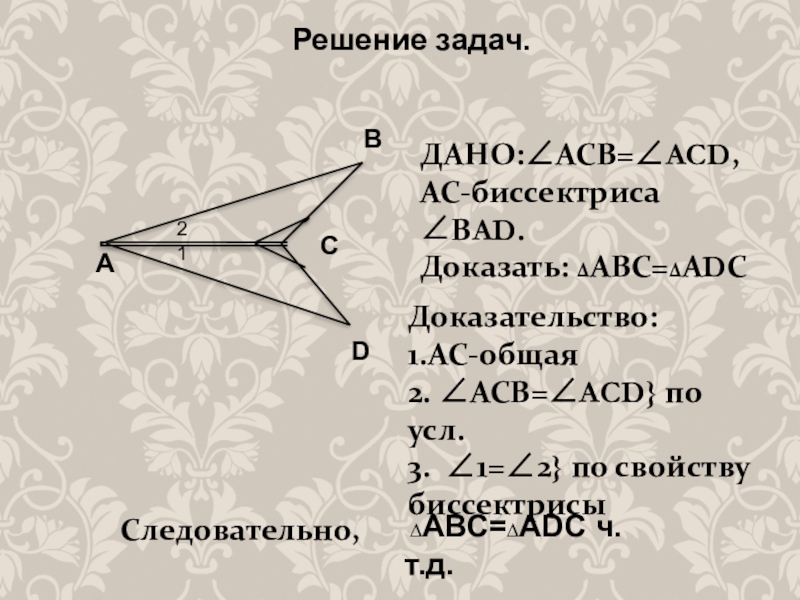
Слайд 4Решение задач.
А
C
D
B
ДАНО:∠АСВ=∠ACD,
АС-биссектриса ∠ВAD.
Доказать: ∆АВС=∆АDС
Доказательство:
1.АС-общая
2. ∠АСВ=∠ACD} по усл.
3. ∠1=∠2} по свойству
биссектрисы
1
2
Следовательно,
∆АВС=∆АDС
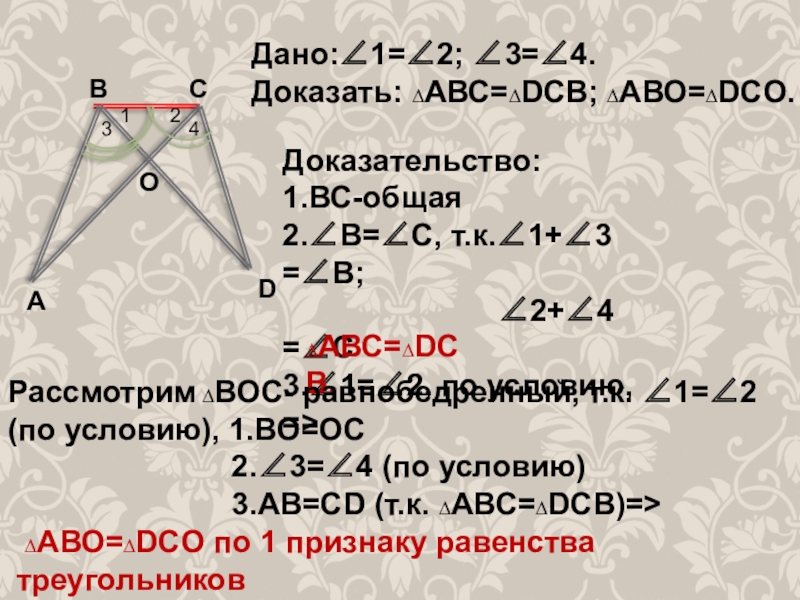
Слайд 51
2
4
3
А
С
В
О
D
Дано:∠1=∠2; ∠3=∠4.
Доказать: ∆АВС=∆DCB; ∆АВО=∆DCO.
Доказательство:
1.ВС-общая
2.∠В=∠С, т.к.∠1+∠3 =∠В;
3.∠1=∠2, по условию, =>
∆АВС=∆DCB.
Рассмотрим ∆ВОС- равнобедренный, т.к. ∠1=∠2
(по условию), 1.ВО=ОС
2.∠3=∠4 (по условию)
3.АВ=СD (т.к. ∆АВС=∆DСВ)=>
∆АВО=∆DCO по 1 признаку равенства
треугольников
Слайд 6Если три стороны одного треугольника
соответственно равны трем сторонам другого
треугольника,
В
А
С
С₁
А₁
В₁
Дано: ∆АВС, ∆А₁В₁С₁,
АВ=₁А₁В₁, ВС=В₁С₁, АС=А₁С₁.
Доказать: ∆АВС=∆А₁В₁С₁
Доказательство:
Приложим ∆АВС к ∆А₁В₁С₁ так, чтобы АВ совместилась с В₁А₁, а вершины С и С₁ находились по разные стороны от прямой А₁В₁.
Слайд 7Возможны три случая:
А₁(А)
С
В₁(В)
С₁
∆СА₁С₁ и ∆СВ₁С₁- равнобедренные,
=>∠1=∠2;∠3=∠4; ∠АВС=∠А₁В₁С₁,
т.к∠АВС=∠2+∠4, ∠А₁В₁С₁=∠1+∠3;
=>∆АВС=∆А₁В₁С₁ (
признаку равенства
треугольников)
2
1
4
3
1. случай
Слайд 9Решение задач.
K
M
L
N
Дано: РKLN=21 cм, РKLMN=26 см.
Найти: NL.
Решение:
1. ∆KLN=∆NML (по третьему
признаку равенства
1. NK=LM
2. KL=NM}(по условию)
3. NL-общая
2. LN=PKLN-½PKLMN=21-½26=21-13=
=8(cм)
Ответ: 8 см.