крепче, умнее.
В.М. Шукшин
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Многогранники.Объемы многогранников
Содержание
- 1. Презентация по математике Многогранники.Объемы многогранников
- 2. Разгадайте ребусы:
- 3. Тема урока:Многогранники.Объемы многогранников.
- 4. Цели урока:Образовательные:-повторить все виды многогранников;-ввести понятие правильного
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Исправить логическую цепочку:Все эти фигуры многогранники:призма;тетраэдр;восьмиугольник;куб.Какую фигуру называем многогранником? Дайте определение.
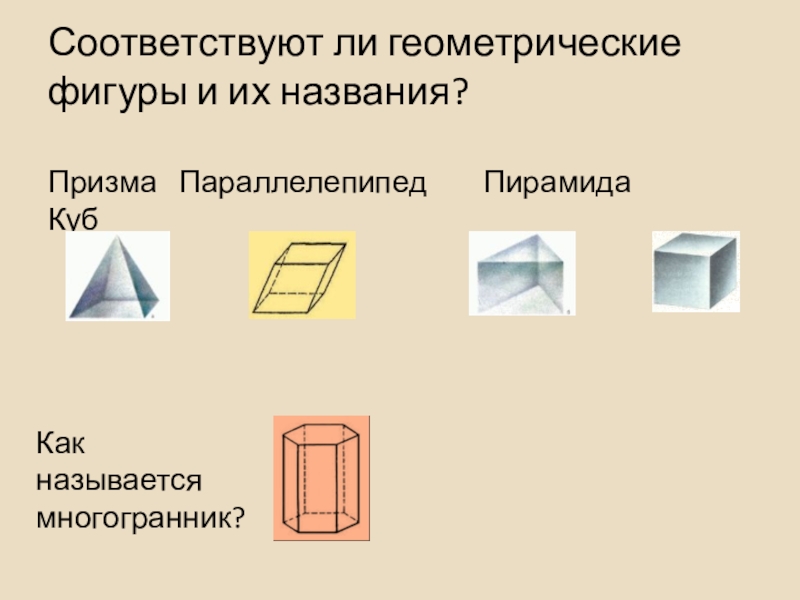
- 17. Соответствуют ли геометрические фигуры и их названия?
- 18. Слайд 18
- 19. Призма Призма — многогранник, две грани которого являются равными
- 20. Слайд 20
- 21. Параллелепипед Параллелепи́пед — призма, основанием которой служит параллелограмм, или
- 22. Слайд 22
- 23. КубКуб или правильный гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы.V=a3Sполн=6a2Sбок=4a2
- 24. Слайд 24
- 25. ПирамидаПирами́да — многогранник, основание которого —многоугольник, а остальные грани — треугольники, имеющие общую вершину.
- 26. Слайд 26
- 27. Усеченная пирамида Усеченной пирамидой называется многогранник, у которого
- 28. Слайд 28
- 29. ТетраэдрТетра́эдр — простейший многогранник, гранями которого являются четыре
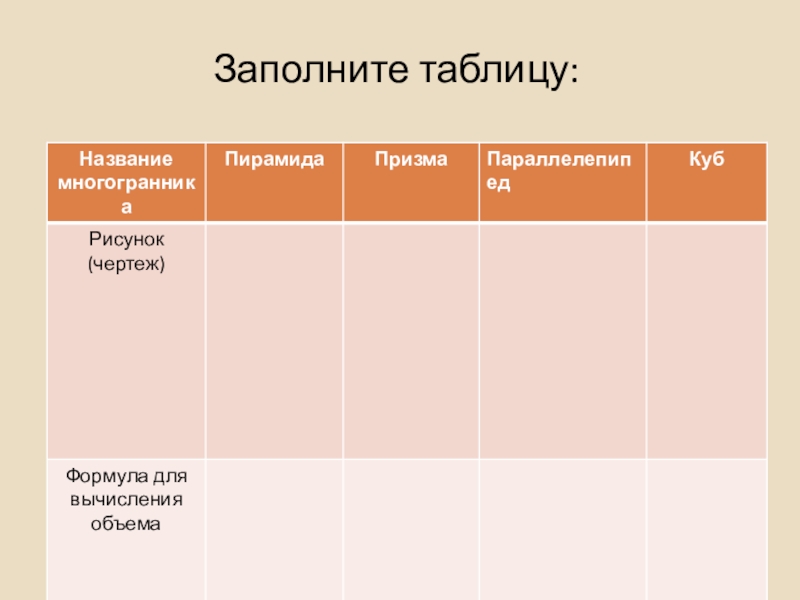
- 30. Заполните таблицу:
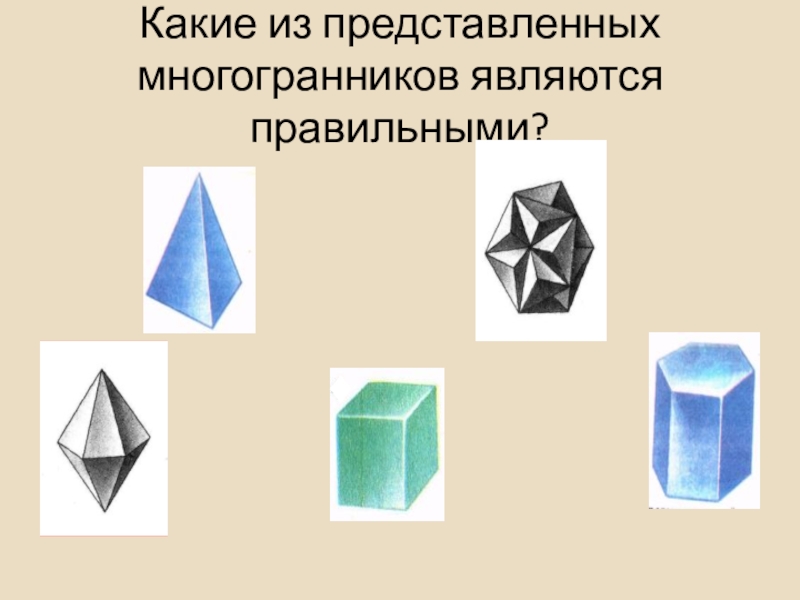
- 31. Какие из представленных многогранников являются правильными?
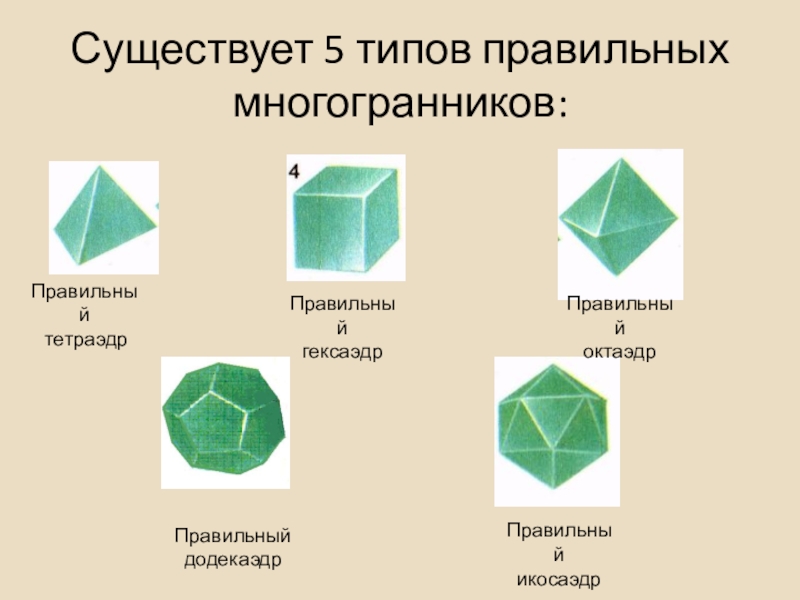
- 32. Существует 5 типов правильных многогранников:Правильный тетраэдрПравильныйгексаэдрПравильныйоктаэдрПравильныйдодекаэдрПравильный икосаэдр
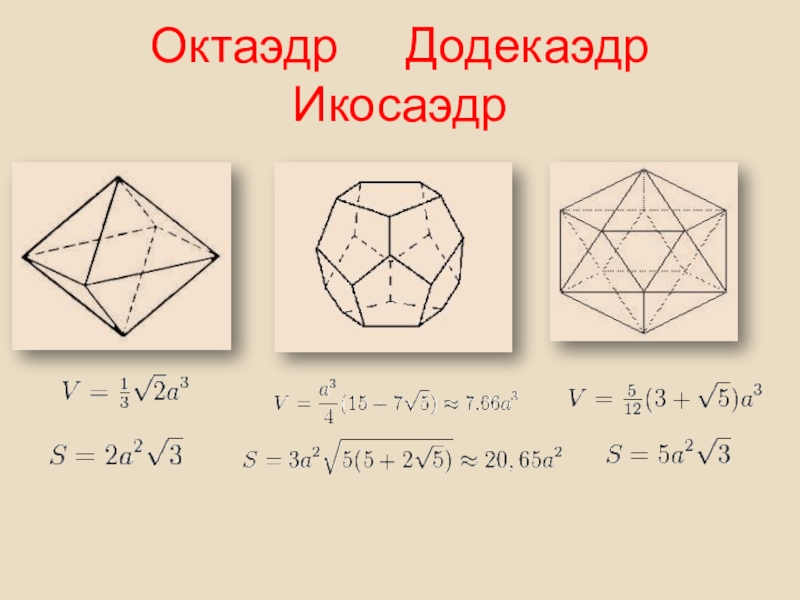
- 33. Октаэдр Додекаэдр Икосаэдр
- 34. Слайд 34
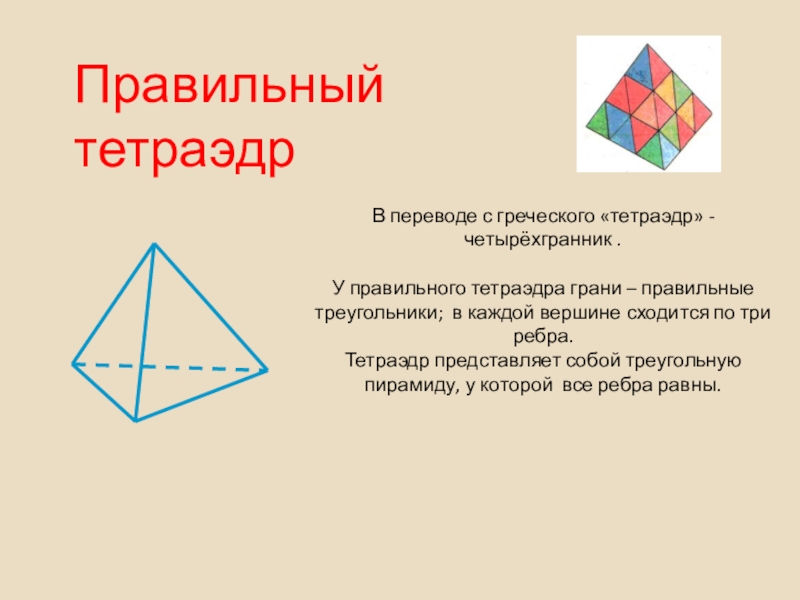
- 35. В переводе с греческого «тетраэдр» - четырёхгранник
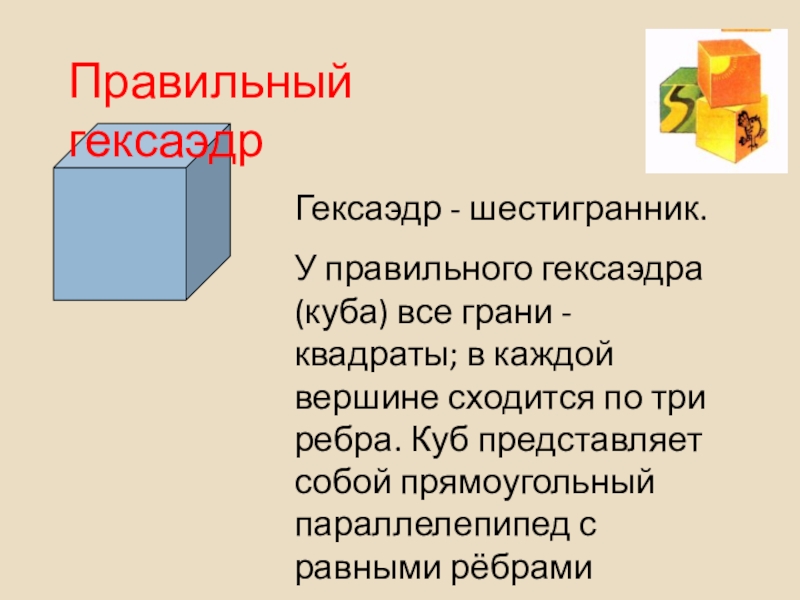
- 36. Гексаэдр - шестигранник.У правильного гексаэдра (куба) все
- 37. Слайд 37
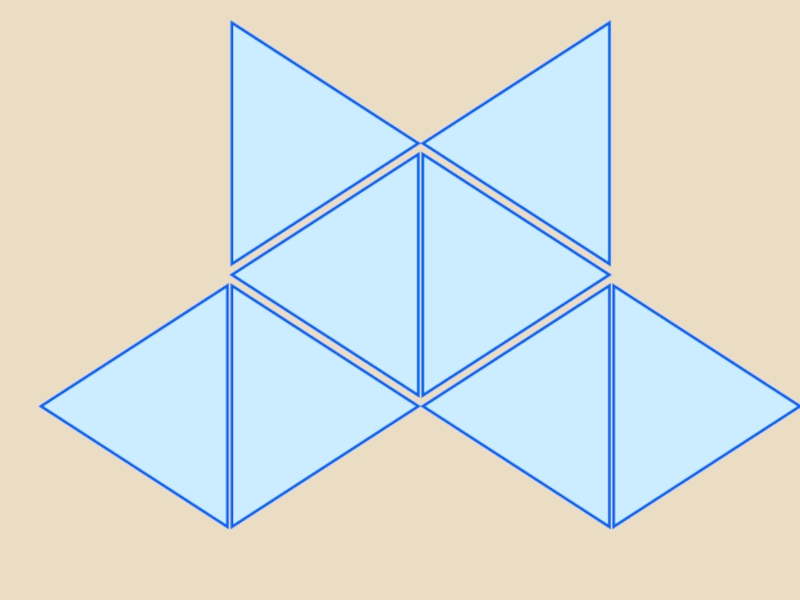
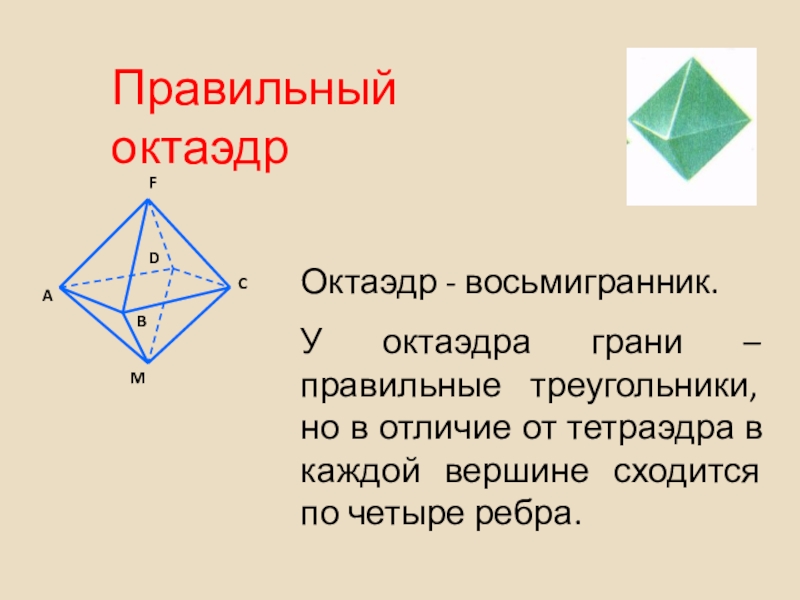
- 38. Правильный октаэдрОктаэдр - восьмигранник.У октаэдра грани –
- 39. Слайд 39
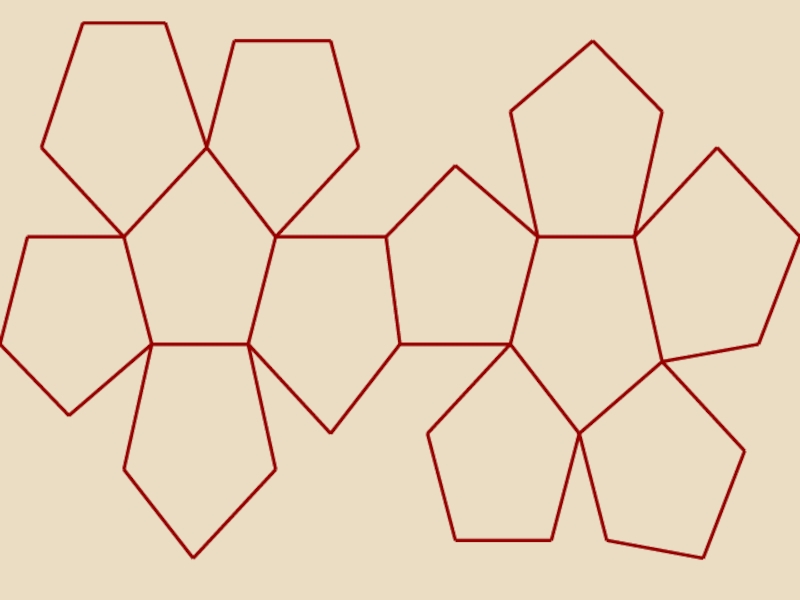
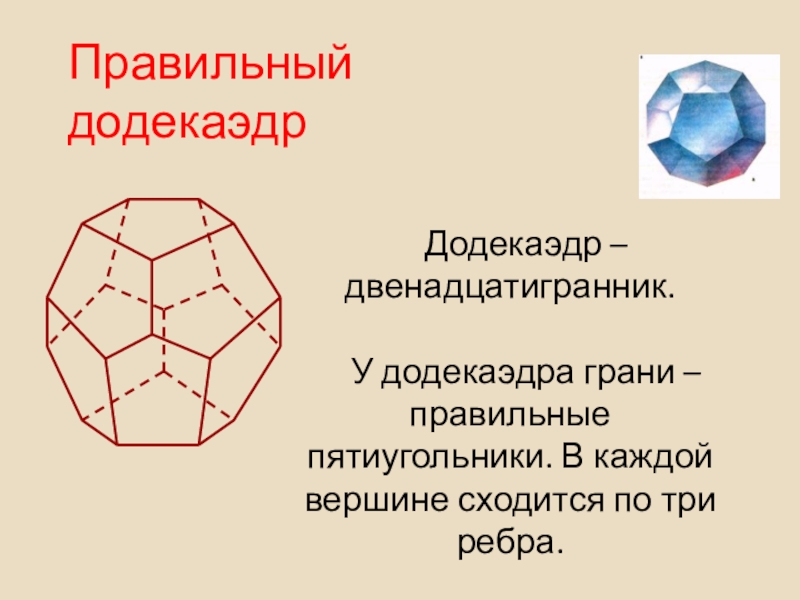
- 40. Правильный додекаэдрДодекаэдр – двенадцатигранник.У додекаэдра грани – правильные пятиугольники. В каждой вершине сходится по три ребра.
- 41. Слайд 41
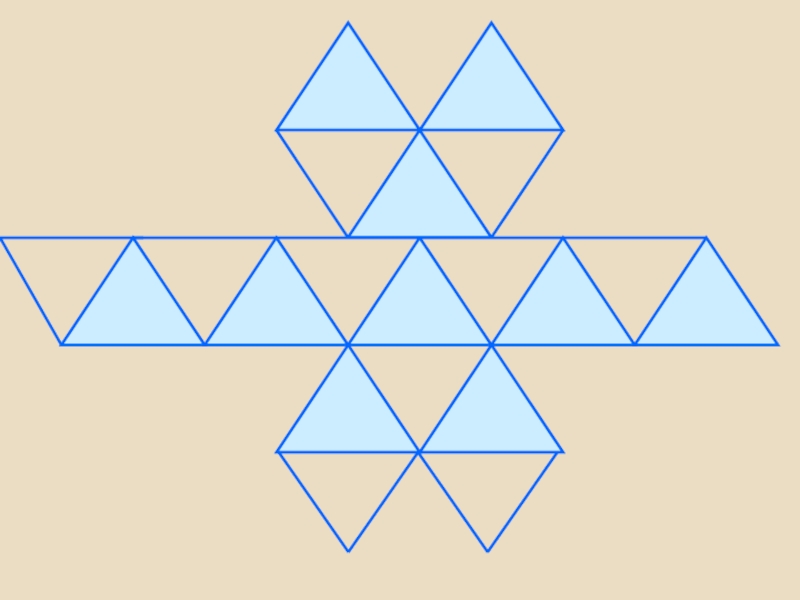
- 42. Правильный икосаэдрИкосаэдр - двадцатигранник.У икосаэдра грани – правильные треугольники. В каждой вершине сходится по пять рёбер.
- 43. Платоновы тела
- 44. Архимедовы телаУсеченный тетраэдрУсеченный кубУсеченный октаэдрУсеченный додекаэдрУсеченный икосаэдрКубоктаэдрИкосододекаэдрРомбокубоктаэдрРомбоикосододекаэдр Ромбоусеченный кубоктаэдрРомбоусеченный икосододекаэдрКурносый кубКурносый додекаэдрпсевдоромбокубоктаэдр
- 45. Слайд 45
Разгадайте ребусы:
Слайд 4Цели урока:
Образовательные:
-повторить все виды многогранников;
-ввести понятие правильного многогранника;
-рассмотреть все пять видов
многогранников.
Развивающие:
-развитие творческих способностей студентов в ходе выполнения самостоятельных заданий;
-развитие логических способностей, памяти, внимания, интуиции, умения быстро ориентироваться в обстановке;
-умение работать с геометрическим материалом, читать чертежи и работать по ним.
Воспитательные:
-умение вести индивидуальную и групповую дискуссию;
-воспитывать чувство ответственности, сплоченности, сознательной дисциплины;
-самостоятельный поиск решения;
-интерес к предмету.
Развивающие:
-развитие творческих способностей студентов в ходе выполнения самостоятельных заданий;
-развитие логических способностей, памяти, внимания, интуиции, умения быстро ориентироваться в обстановке;
-умение работать с геометрическим материалом, читать чертежи и работать по ним.
Воспитательные:
-умение вести индивидуальную и групповую дискуссию;
-воспитывать чувство ответственности, сплоченности, сознательной дисциплины;
-самостоятельный поиск решения;
-интерес к предмету.
Слайд 16Исправить логическую цепочку:
Все эти фигуры многогранники:
призма;
тетраэдр;
восьмиугольник;
куб.
Какую фигуру называем многогранником? Дайте определение.
Слайд 17Соответствуют ли геометрические фигуры и их названия? Призма Параллелепипед
Пирамида Куб
Как называется
многогранник?
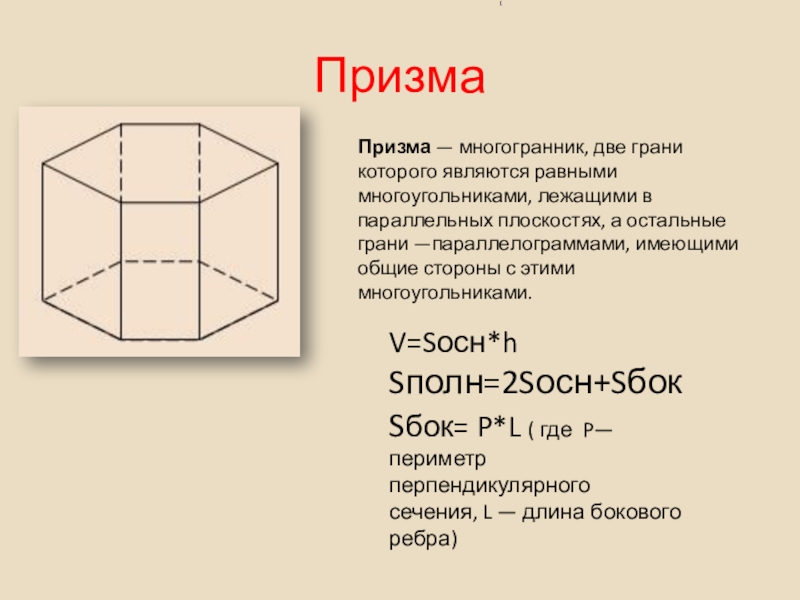
Слайд 19Призма
Призма — многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных
плоскостях, а остальные грани —параллелограммами, имеющими общие стороны с этими многоугольниками.
V=Sосн*h
Sполн=2Sосн+Sбок
Sбок= P*L ( где P— периметр перпендикулярного сечения, L — длина бокового ребра)
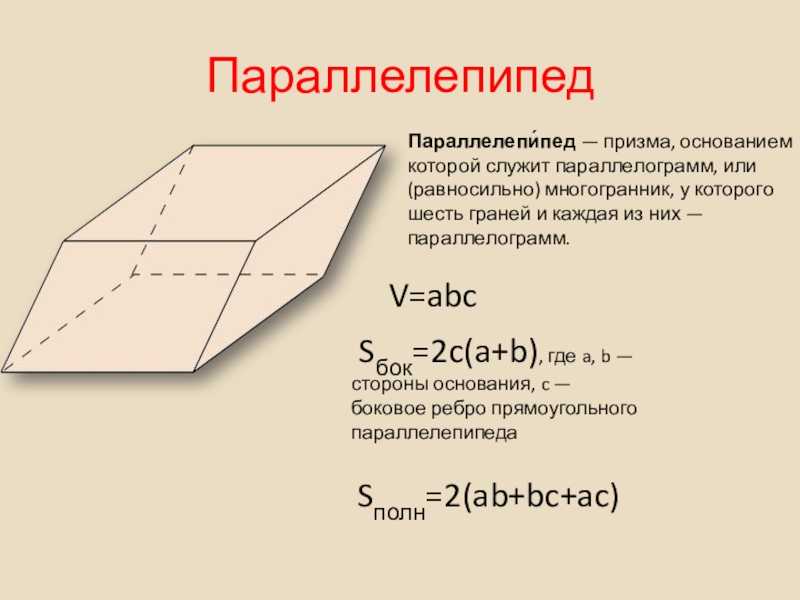
Слайд 21Параллелепипед
Параллелепи́пед — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого
шесть граней и каждая из них — параллелограмм.
V=abc
Sбок=2c(a+b), где a, b — стороны основания, c — боковое ребро прямоугольного параллелепипеда
Sполн=2(ab+bc+ac)
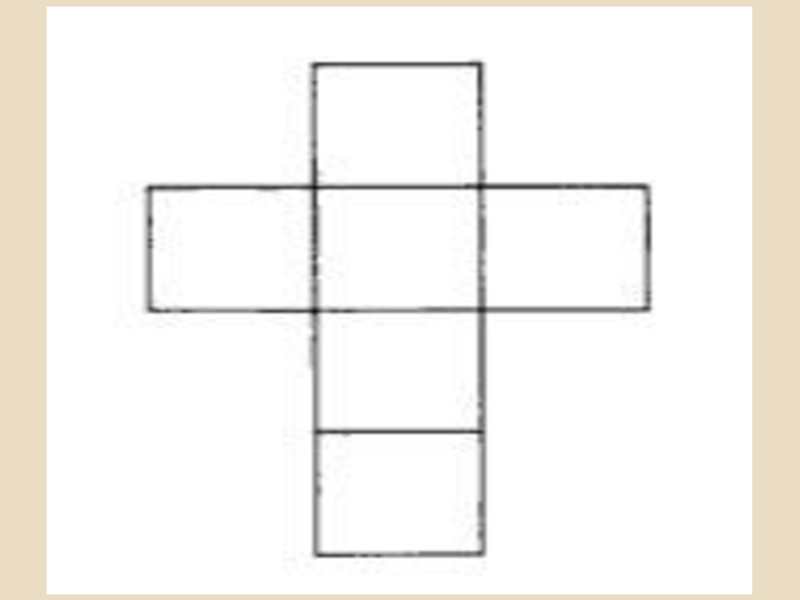
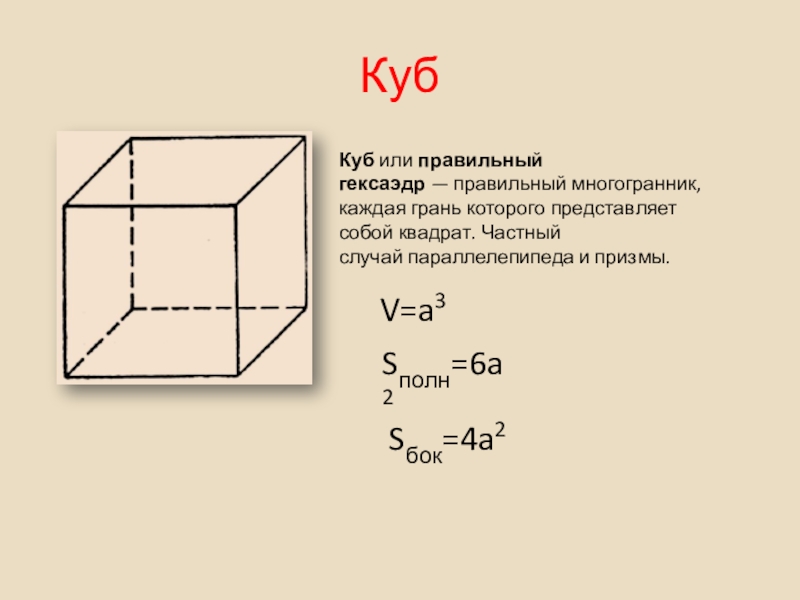
Слайд 23Куб
Куб или правильный гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы.
V=a3
Sполн=6a2
Sбок=4a2
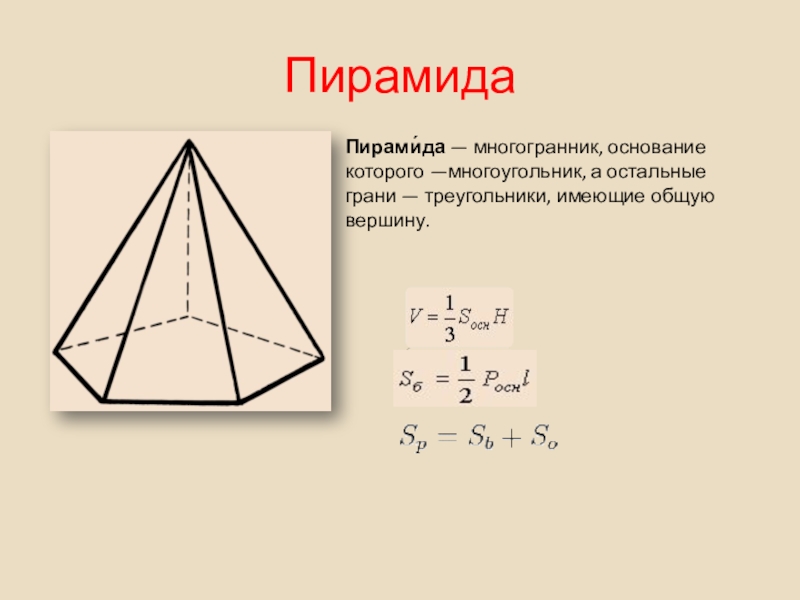
Слайд 25Пирамида
Пирами́да — многогранник, основание которого —многоугольник, а остальные грани — треугольники, имеющие общую вершину.
Слайд 27Усеченная пирамида
Усеченной пирамидой называется многогранник, у которого вершинами служат вершины основания
и вершины ее сечения плоскостью, параллельной основанию.
Sп=Sб+S1+S2 ,
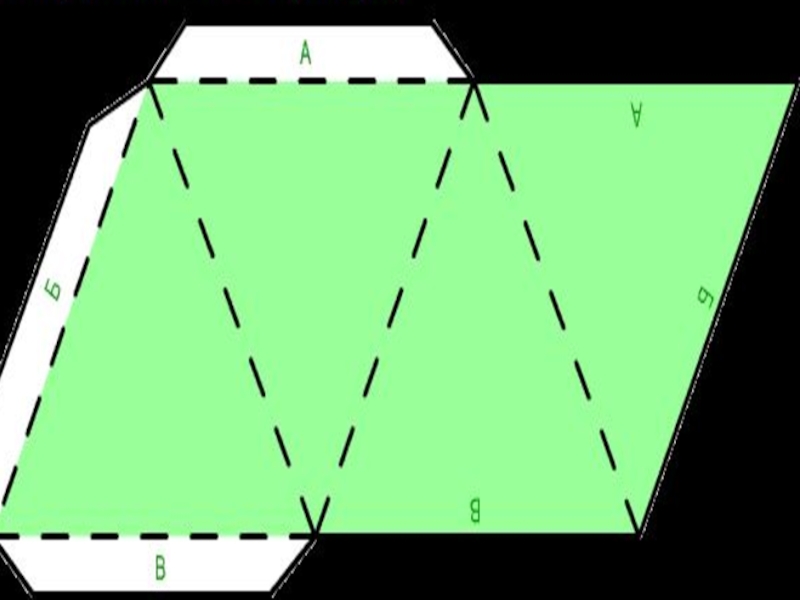
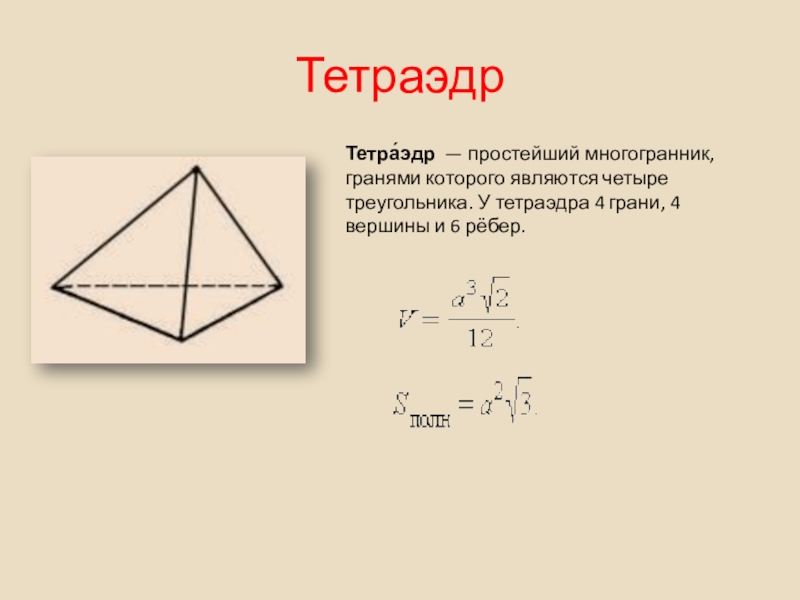
Слайд 29Тетраэдр
Тетра́эдр — простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра 4
грани, 4 вершины и 6 рёбер.
Слайд 32Существует 5 типов правильных многогранников:
Правильный
тетраэдр
Правильный
гексаэдр
Правильный
октаэдр
Правильный
додекаэдр
Правильный
икосаэдр
Слайд 35В переводе с греческого «тетраэдр» - четырёхгранник .
У правильного тетраэдра грани – правильные треугольники; в каждой вершине сходится по три ребра.
Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны.
Правильный тетраэдр
Слайд 36Гексаэдр - шестигранник.
У правильного гексаэдра (куба) все грани -квадраты; в каждой
вершине сходится по три ребра. Куб представляет собой прямоугольный параллелепипед с равными рёбрами
Правильный гексаэдр
Слайд 38Правильный октаэдр
Октаэдр - восьмигранник.
У октаэдра грани – правильные треугольники, но в
отличие от тетраэдра в каждой вершине сходится по четыре ребра.
Слайд 40Правильный додекаэдр
Додекаэдр – двенадцатигранник.
У додекаэдра грани – правильные пятиугольники. В каждой
вершине сходится по три ребра.
Слайд 42Правильный икосаэдр
Икосаэдр - двадцатигранник.
У икосаэдра грани – правильные треугольники. В каждой
вершине сходится по пять рёбер.
Слайд 44Архимедовы тела
Усеченный тетраэдр
Усеченный куб
Усеченный октаэдр
Усеченный додекаэдр
Усеченный икосаэдр
Кубоктаэдр
Икосододекаэдр
Ромбокубоктаэдр
Ромбоикосододекаэдр
Ромбоусеченный кубоктаэдр
Ромбоусеченный икосододекаэдр
Курносый куб
Курносый
додекаэдр
псевдоромбокубоктаэдр
