- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Многогранники и философская картина мира
Содержание
- 1. Презентация по математике Многогранники и философская картина мира
- 2. Правильные многогранники играли большую роль в философии древних греков
- 3. Правильным называется такой многогранник, все грани которого
- 4. Тетраэдр (четырёхгранник – от греческого «тетра», т.е. четыре)
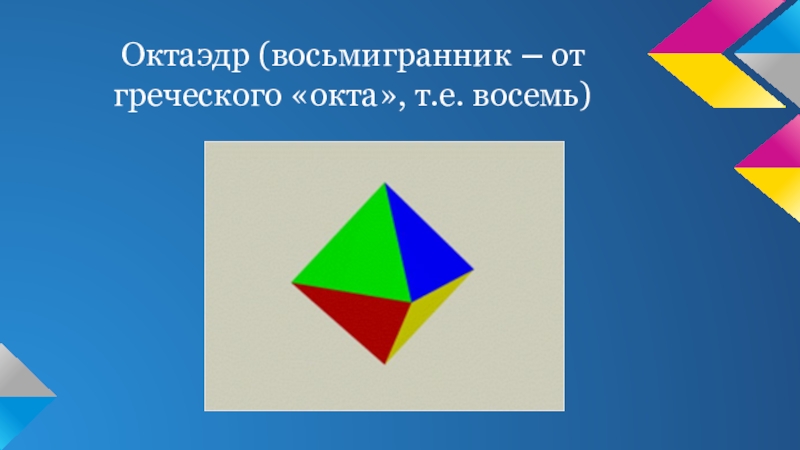
- 5. Октаэдр (восьмигранник – от греческого «окта», т.е. восемь)
- 6. Икосаэдр (двадцатигранник – от греческого «икос», т.е. двадцать)
- 7. Гексаэдр или куб (шестигранник – от греческого «гекса», т.е. шесть)
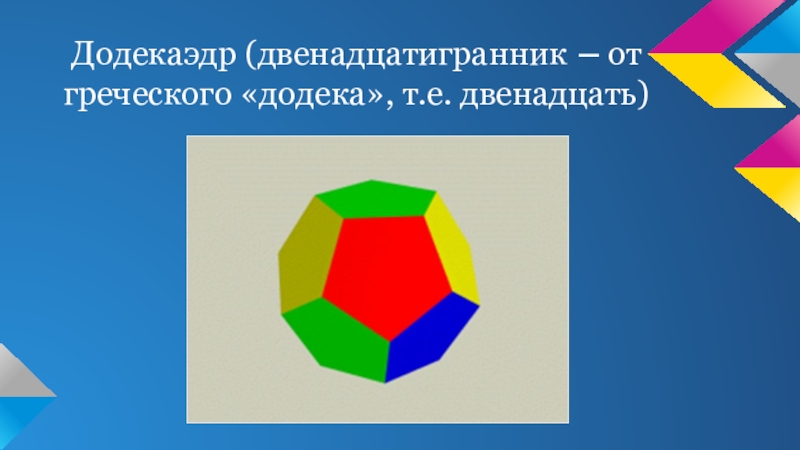
- 8. Додекаэдр (двенадцатигранник – от греческого «додека», т.е. двенадцать)
- 9. Если построить все пять правильных многогранников, сосчитать
- 10. ПлатонПодробно описал свойства правильных многогранников древнегреческий учёный,
- 11. Философия ПлатонаТетраэдр символизировал огонь, т.к. его вершина устремлена вверх
- 12. Философия ПлатонаКуб или гексаэдр символизировал – землю, как самый «устойчивый»
- 13. Философия ПлатонаОктаэдр символизирует воздух, как самый «воздушный»
- 14. Философия ПлатонаИкосаэдр символизирует воду, т.к. он самый «обтекаемый»
- 15. Философия ПлатонаВсей вселенной была приписана форма додекаэдра,
- 16. Авторские фотографии правильных многогранников,сделанные из магнитного конструктора (додекаэдр выполнить не удалось)
- 17. ЗаключениеПравильные многогранники играли важную роль в философии древних греков, в частности, философа Платона
Правильные многогранники играли большую роль в философии древних греков
Слайд 3Правильным называется такой многогранник, все грани которого равны между собой и
при этом являются правильными многоугольниками.
В «Началах» Евклида находится строгое доказательство того, что существует только пять выпуклых правильных многогранников, а их гранями могут быть только три типа правильных многоугольников: треугольники, квадраты и пентагоны (правильные пятиугольники).
В «Началах» Евклида находится строгое доказательство того, что существует только пять выпуклых правильных многогранников, а их гранями могут быть только три типа правильных многоугольников: треугольники, квадраты и пентагоны (правильные пятиугольники).
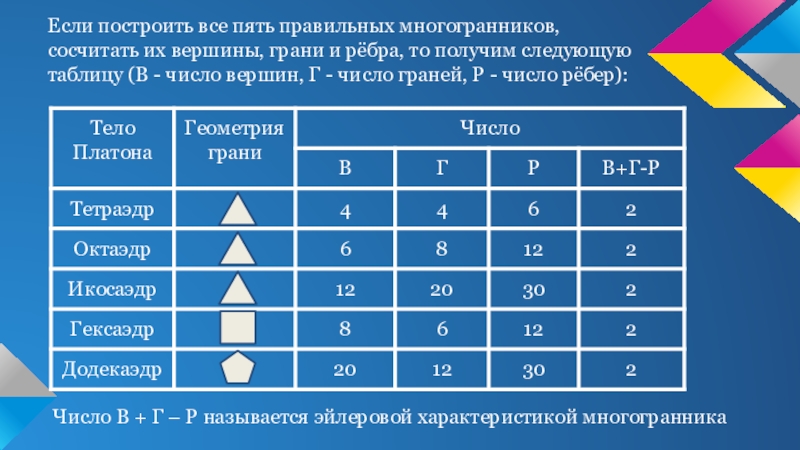
Слайд 9Если построить все пять правильных многогранников, сосчитать их вершины, грани и
рёбра, то получим следующую таблицу (В - число вершин, Г - число граней, Р - число рёбер):
Число В + Г – Р называется эйлеровой характеристикой многогранника
Слайд 10Платон
Подробно описал свойства правильных многогранников древнегреческий учёный, философ-идеалист Платон
(428 –348
до н.э.), в учении которого они играли важную роль. Поэтому эти многогранники носят название «платоновых тел».
Слайд 15Философия Платона
Всей вселенной была приписана форма додекаэдра, т. к. мы живём
внутри небесного свода, имеющего форму поверхности правильного додекаэдра
Слайд 16Авторские фотографии правильных многогранников,сделанные из магнитного конструктора (додекаэдр выполнить не удалось)
Слайд 17Заключение
Правильные многогранники играли важную роль в философии древних греков, в частности,
философа Платона