- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Математические софизмы и парадоксы
Содержание
- 1. Презентация по математике Математические софизмы и парадоксы
- 2. Софизм – /от греческого
- 3. Цель моей работы - доказательство того, что
- 4. История возникновения софизмов
- 5. Математический софизм – удивительное
- 6. Математические софизмы: АРИФМЕТИЧЕСКИЕАЛГЕБРАИЧЕСКИЕГЕОМЕТРИЧЕСКИЕ
- 7. АРИФМЕТИЧЕСКИЕ СОФИЗМЫАрифметика - (греч. arithmetika, от arithmys
- 8. «2 × 2 = 5»2 × 2
- 9. «2 + 2 = 5»Чтобы доказать,
- 10. «5 = 6» 5 = 6Возьмём верное равенство: 35
- 11. «Пропавший рубль» Три подруги зашли в кафе
- 12. АЛГЕБРАИЧЕСКИЕ СОФИЗМЫАлгебра — один из больших разделов
- 13. «Каждое число равно своему удвоенному значению»Возьмем верное
- 14. Уравнение x-a=0 не имеет корнейДано уравнение: x-a=0
- 15. «Два неодинаковых натуральных числа равны
- 16. ГЕОМЕТРИЧЕСКИЕ СОФИЗМЫГеометрические софизмы – это умозаключения или
- 17. Задача о треугольникеДан прямоугольный
- 18. Слайд 18
- 19. “В любой окружности хорда, не проходящая через
- 20. Слайд 20
- 21. Типичные ошибки при решении софизмовЗапрещенные действие.Пренебрежение условием теорем, формул и правил.Ошибочный чертеж.Опора на ошибочные умозаключения.
- 22. Что такое парадокс? Парадокс (греч. "пара" - "против",
- 23. Я расскажу о парадоксах,
- 24. Парадокс кучиИмеется утверждение: «Разница между кучей
- 25. Парадокс Эпименида Критянин Эпименид сказал: "Все критяне лжецы".
- 26. «Два слова, спасшие жизнь»Во время франко-прусской войны
- 27. ЗаключениеПонять софизм или парадокс как таковой (решить
- 28. Литература:1. «Математические софизмы». Книга для учащихся 7-11
Слайд 1 МОУ
«Нарминская средняя школа»
МАТЕМАТИЧЕСКИЕ
И ПАРАДОКСЫ
Выполнила: учащаяся 11 класса
Кутинова Юлия
Руководитель: учитель математики
Мирионкова Людмила Николаевна
Слайд 2 Софизм – /от греческого sophisma – хитрая выдумка/
Слайд 3Цель моей работы - доказательство того, что софизмы являются не просто
Задачи: рассмотреть математические, алгебраические, геометрические софизмы с точки зрения их важности для изучения математики.
Найти ошибки в представленных софизмах.
Показать софизмы из жизни и современной практики.
Рассмотреть парадоксы и выяснить чем они отличаются от софизмов.
Слайд 4
История возникновения
софизмов
Возникновение софизмов обычно связывается с философией софистов
Слайд 5 Математический софизм – удивительное утверждение, в доказательстве которого
Математические софизмы приучают быть внимательными при решении задач, тщательно следить за точностью формулировок, правильностью чертежей, за законностью математических операций.
Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления.
Слайд 7АРИФМЕТИЧЕСКИЕ СОФИЗМЫ
Арифметика - (греч. arithmetika, от arithmys — число), наука о
Так что же такое арифметические софизмы?
Арифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.
Слайд 8«2 × 2 = 5»
2 × 2 =5
Возьмем верное равенство:
Вынеся за скобки общие множители, получим:
4 • (1:1) = 5 • (1: 1)
Так как 1: 1 = 1, то имеем
4 • 1 = 5 • 1, а значит 4 = 5 , но 4 = 2 × 2
Значит 2 × 2 =5
В чем ошибка?
Слайд 9 «2 + 2 = 5»
Чтобы доказать, что 2 + 2
Начнём с равенства: 16-36 = 25-45
Прибавим к обеим частям 20,25, получим:
16-36+20,25=25-45+20,25
Заметим, что в обеих частях равенства стоит квадрат разности:
4² - 2 • 4 • 4,5 + 4,5²=5 ² - 2 • 5 • 4,5 + 4,5
Получим: (4 - 4,5)²=(5 - 4,5)²
Извлекаем корень из обеих частей равенства, получим: 4 - 4,5 = 5 - 4,5
Значит 4=5.
В чем ошибка?
Слайд 10«5 = 6»
5 = 6
Возьмём верное равенство:
35 + 10 – 45
Вынесем общие множители левой и правой частей за скобки. Получим:
5 (7 + 2 – 9) = 6 (7 + 2 – 9).
Разделим обе части этого равенства на общий множитель (заключённый в скобки).
Получаем 5 = 6.
В чём ошибка?
Слайд 11«Пропавший рубль»
Три подруги зашли в кафе выпить по чашке кофе.
Однако хозяин кафе почему-то решил, что поданный на этот столик кофе стоит 25 рублей, и велел вернуть посетительницам 5 рублей.
Официант взял деньги и побежал догонять подруг, но пока бежал, подумал, что им будет трудно делить на троих 5 рублей, и поэтому решил отдать им по 1 рублю, а два рубля оставить себе. Так и сделал.
Что же получилось? Подруги заплатили по 9 рублей.
9 × 3 = 27 рублей, да два рубля осталось у официанта.
А где еще 1 рубль?
Слайд 12АЛГЕБРАИЧЕСКИЕ СОФИЗМЫ
Алгебра — один из больших разделов математики, принадлежащий наряду с
То есть алгебраические софизмы – намеренно скрытые ошибки в уравнениях и выражениях с переменными.
Слайд 13«Каждое число равно своему удвоенному значению»
Возьмем верное равенство:
В левой части вынесем общий множитель за скобки, а в правой воспользуемся формулой разность квадратов:
a (a – a) = (a + a )( a – a )
Поделим на общий множитель (a – a );
Получим a = a + a
a = 2 a.
Слайд 14Уравнение x-a=0 не имеет корней
Дано уравнение: x-a=0
Разделим всё на x-a,
Это равенство неверное, следовательно исходное уравнение не имеет корней.
В чем ошибка?
Слайд 15
«Два неодинаковых натуральных числа равны между собой»
Решим систему двух уравнений:
Сделаем это подстановкой у из второго уравнения в первое.
Получаем х + 8 – х = 6, откуда
8=6
Где же ошибка?
Слайд 16ГЕОМЕТРИЧЕСКИЕ СОФИЗМЫ
Геометрические софизмы – это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую
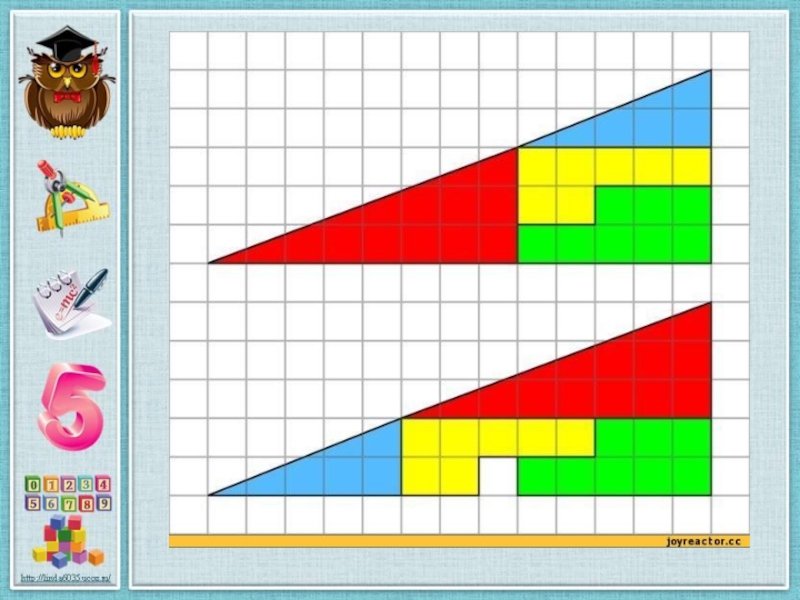
Слайд 17 Задача о треугольнике
Дан прямоугольный треугольник 13×5 клеток, составленный
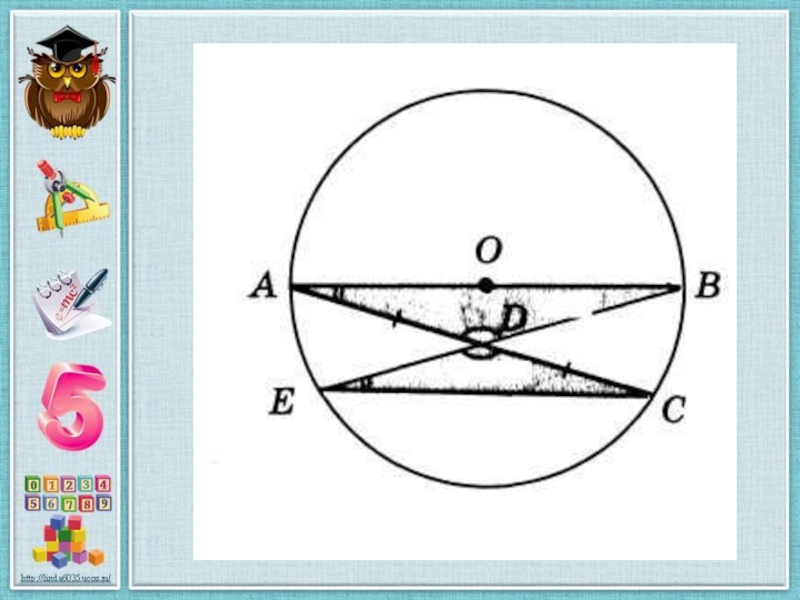
Слайд 19“В любой окружности хорда, не проходящая через её центр, равна её
В произвольной окружности проводим диаметр АВ и хорду АС. Через середину D этой хорды и точку В проводим хорду BE. Соединив точки С и Е, получаем два треугольника ABD и CDE. Углы ВАС и СЕВ равны как вписанные в одну и ту же окружность, опирающиеся на одну и ту же дугу; углы ADB и CDE равны как вертикальные; стороны AD и CD равны по построению. Отсюда заключаем, что треугольники ABD и CDE равны (по стороне и двум углам).
Но соответствующие стороны равных треугольников равны АВ=СЕ
получается, что диаметр окружности оказывается равным некоторой (не проходящей через центр окружности) хорде, что противоречит утверждению о том, что диаметр больше всякой не проходящей через центр окружности хорды.
Слайд 21Типичные ошибки при решении софизмов
Запрещенные действие.
Пренебрежение условием теорем, формул и правил.
Ошибочный
Опора на ошибочные умозаключения.
Слайд 22Что такое парадокс?
Парадокс (греч. "пара" - "против", "докса" - "мнение") близок софизму С
Математический парадокс – высказывание, которое в данной теории равным образом может быть доказано и как истинна, и как ложь. Парадокс — это рассуждение, доказывающее как истинность, так и ложность некоторого суждения, иными словами, доказывающее как это суждение, так и его отрицание.
Слайд 23 Я расскажу о парадоксах, которые затрагивают сферы логики
Слайд 24 Парадокс кучи
Имеется утверждение: «Разница между кучей и не кучей не
Слайд 25Парадокс Эпименида
Критянин Эпименид сказал: "Все критяне лжецы". Он сам критянин, соответственно,
Слайд 26«Два слова, спасшие жизнь»
Во время франко-прусской войны произошел следующий случай. Один
- Вам, молодой человек, - сказали они офицеру, - предлагается в виде особой милости самому выбрать род казни: или смерть через повешенье, или расстрел. Для этого мы предлагаем вам произнести какую-нибудь фразу, заключающую в себе или явную ложь или явную правду. При этом заметьте, что за сказанную вами правду вы будете повешены, а за неправду вас расстреляют.
Все это было, конечно, очень жестоко, немилосердно, но странное дело! По мере того как молодой человек слушал бесстрастную речь своих судей, его бледное умное лицо прояснилось все более и более, и, наконец, после некоторого размышления он медленно произнес: «Меня расстреляют».
Слайд 27Заключение
Понять софизм или парадокс как таковой (решить его и найти ошибку)
Благодаря софизмам и парадоксам можно научиться искать ошибки в рассуждениях других, научится грамотно строить свои рассуждения и логические объяснения.
Слайд 28Литература:
1. «Математические софизмы». Книга для учащихся 7-11 классов. Авторы: А.Г. Мадера,
2. «Математическая шкатулка». Автор: Ф.Ф. Нагибин. Государственное учебно-педагогическое издательство министерства просвещения РСФСР 1961.
3. «Математика после уроков». Пособие для учителей. Авторы: М.Б.Балк, Г.Д.Балк. Москва «Просвещение», 1971.
4. «В царстве смекалки». Автор: Е. И. Игнатьев. 1984.