- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Лист Мёбиуса
Содержание
- 1. Презентация по математике Лист Мёбиуса
- 2. Август Фердинанд МёбиусМЕБИУС Август Фердинанд (1790-1868), немецкий
- 3. Лента Мёбиуса- простейшая односторонняя поверхность, рассмотренная А.
- 4. представление о ленте МёбиусаЛента Мёбиуса - бумажная
- 5. Топологические свойства1. Односторонность - топологическое свойство листа
- 6. Лист Мебиуса в науке и техникеЛента Мебиуса
- 7. Лист Мёбиуса в искусстве и технологииЛист Мёбиуса
- 8. серебряное колечко в виде листа Мёбиуса
- 9. Подобные объектыБлизким «странным» геометрическим объектом является бутылка
- 10. памятник "Ленте Мёбиуса"Установлен в МОСКВЕНа комсомольском проспекте около кинотеатра «Горизонт»
- 11. Лист Мёбиуса - вот наглядный образец Того,
- 12. Литература Атанасян, Л. С, Гуревич, Г. Б.
Август Фердинанд МёбиусМЕБИУС Август Фердинанд (1790-1868), немецкий математик. Труды по геометрии. Установил существование односторонних поверхностей (лист Мёбиуса).
Слайд 2Август Фердинанд Мёбиус
МЕБИУС Август Фердинанд (1790-1868), немецкий математик. Труды по геометрии.
Установил существование односторонних поверхностей
(лист Мёбиуса).
(лист Мёбиуса).
Слайд 3Лента Мёбиуса
- простейшая односторонняя поверхность, рассмотренная А. Мёбиусом; получается при склеивании
двух противоположных сторон АВ и А'В' прямоугольника АВВ'А' так, что точки А и В совмещаются соответственно с точками В' и А'.
Слайд 4представление о ленте Мёбиуса
Лента Мёбиуса - бумажная лента, повернутая одним концом
на пол-оборота (то есть на 180 градусов), и склеенная с его другим концом.
Поверхность ленты Мёбиуса имеет только одну сторону.
Следуют удивительные превращения ленты. Если разрезать ее вдоль, точно посередине -получится не две, а одна лента. А вот если разрезать ленту на расстоянии 1/3 ее ширины от края, то получаются два кольца - но! -одно большое и сцепленное с ним маленькое. Если же разрезать еще и маленькое кольцо вдоль посередине, то у вас окажется весьма «затейливое» переплетение двух колец - одинаковых по размеру, но разных по ширине.
Поверхность ленты Мёбиуса имеет только одну сторону.
Следуют удивительные превращения ленты. Если разрезать ее вдоль, точно посередине -получится не две, а одна лента. А вот если разрезать ленту на расстоянии 1/3 ее ширины от края, то получаются два кольца - но! -одно большое и сцепленное с ним маленькое. Если же разрезать еще и маленькое кольцо вдоль посередине, то у вас окажется весьма «затейливое» переплетение двух колец - одинаковых по размеру, но разных по ширине.
Слайд 5Топологические свойства
1. Односторонность - топологическое свойство листа Мёбиуса, характерное только для
него.
2. Непрерывность - с топологической точки зрения круг неотличим от квадрата, потому что их легко преобразовать один в другой, не нарушая непрерывность.
3. Ориентированность — свойство, отсутствующее у листа Мёбиуса.
4. Связность - чтобы разделить квадрат на две части, нам потребуется только один разрез. Но вот чтобы располовинить кольцо, потребуется уже два разреза. Что касается листа Мёбиуса, то количество связей меняется в зависимости от смены количества оборотов ленты
2. Непрерывность - с топологической точки зрения круг неотличим от квадрата, потому что их легко преобразовать один в другой, не нарушая непрерывность.
3. Ориентированность — свойство, отсутствующее у листа Мёбиуса.
4. Связность - чтобы разделить квадрат на две части, нам потребуется только один разрез. Но вот чтобы располовинить кольцо, потребуется уже два разреза. Что касается листа Мёбиуса, то количество связей меняется в зависимости от смены количества оборотов ленты
Слайд 6Лист Мебиуса в науке и технике
Лента Мебиуса используется во многих изобретениях.
18 лет назад ленточке нашли совсем другое применение она стала выполнять роль пружины, вот только пружины особенной. Как известно, взведенная пружина срабатывает в противоположном направлении. Лента Мебиуса же, поправив все законы направления , срабатывания не меняет, подобно механизмам с двумя устойчивыми положениями
Слайд 7Лист Мёбиуса в искусстве и технологии
Лист Мёбиуса служил вдохновением для скульптур
и для графического искусства. Эшер был одним из художников, кто особенно любил его и посвятил несколько своих литографий этому математическому объекту. Одна из известных — лист Мёбиуса II, показывает муравьёв, ползающих по поверхности ленты Мёбиуса.
Слайд 9Подобные объекты
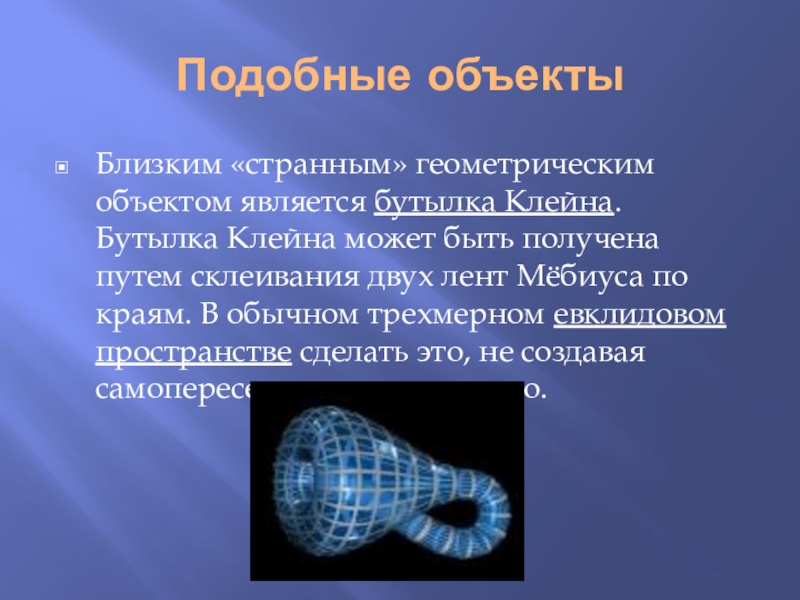
Близким «странным» геометрическим объектом является бутылка Клейна. Бутылка Клейна может
быть получена путем склеивания двух лент Мёбиуса по краям. В обычном трехмерном евклидовом пространстве сделать это, не создавая самопересечения, невозможно.
Слайд 10памятник "Ленте Мёбиуса"
Установлен в МОСКВЕ
На комсомольском
проспекте
около кинотеатра
«Горизонт»
Слайд 11Лист Мёбиуса - вот наглядный образец Того, что и конец-то - не
конец
Любого дела, а лишь новое начало с того,
Что в деле первом окончание обозначало!
Он говорит тому, кто хочет слышать,
Что как ни трудно, всё же надо выжить,
Отчаянье из сердца выжечь
И выйти из очередной житейской передряги -
Для бодрости хлебнув глоток из фляги,
Взять да и минус поменять на плюс,
Чтоб полной жизнью вновь забился пульс.
Слайд 12Литература
Атанасян, Л. С, Гуревич, Г. Б. Геометрия. - Ч. 2.
- М: Просвещение, 1976.
Квант: научно-популярный журнал. - 1975, № 7; 1977, № 7.
Смирнов, С. Г. Библиотека «Математическое просвещение». - Вып. 27.-М.: МЦНМО, 2003.
Возможности сети «ИНТЕРНЕТ».
Квант: научно-популярный журнал. - 1975, № 7; 1977, № 7.
Смирнов, С. Г. Библиотека «Математическое просвещение». - Вып. 27.-М.: МЦНМО, 2003.
Возможности сети «ИНТЕРНЕТ».