- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике: ЛЕММА О РАВНЫХ ОКРУЖНОСТЯХ
Содержание
- 1. Презентация по математике: ЛЕММА О РАВНЫХ ОКРУЖНОСТЯХ
- 2. ЛЕММАПусть H — ортоцентр (точка пересечения высот) треугольника
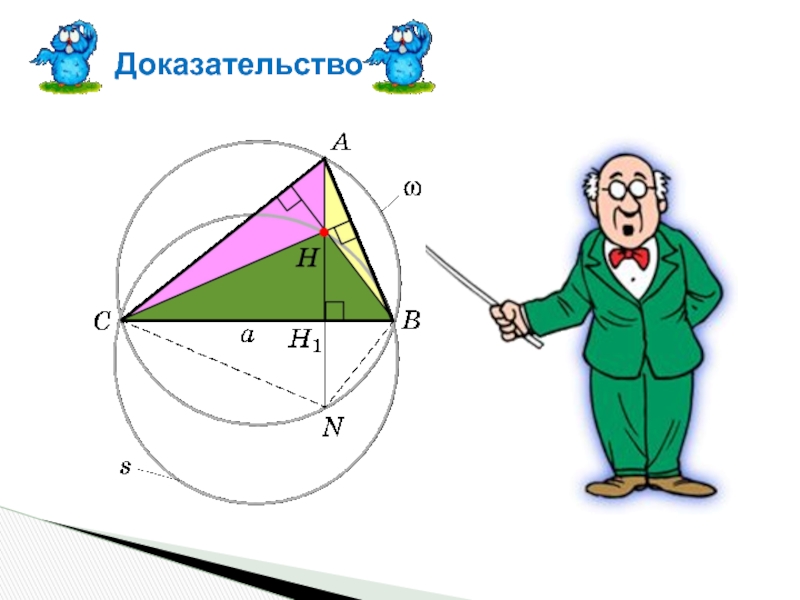
- 3. Доказательство
- 4. Задача 1Бывает ли, что окружности ω и
- 5. Задача 2Медиану АМ треугольника АВС удвоили и получили точку Т. Докажите, что Т ∈ s.
- 6. Доказательство.
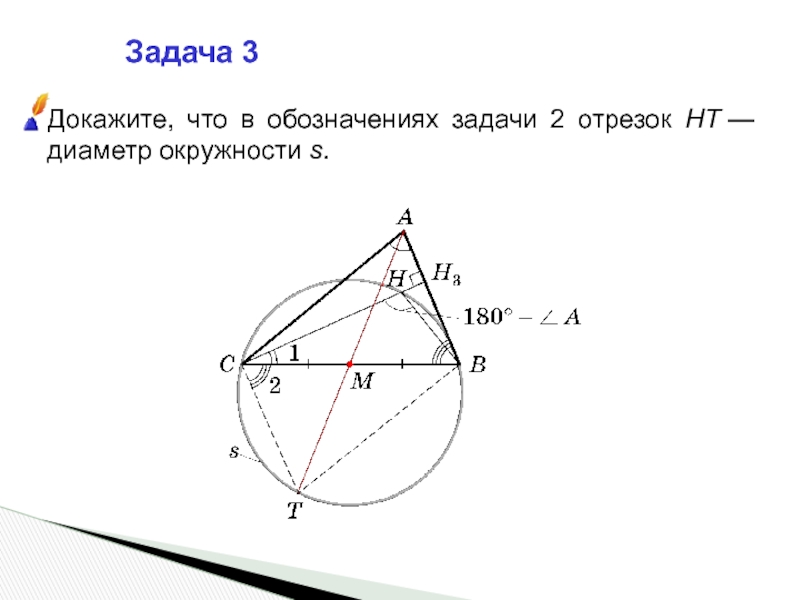
- 7. Задача 3Докажите, что в обозначениях задачи 2 отрезок HT — диаметр окружности s.
- 8. Доказательство. Из треугольника BCH3 находим, что ∠1
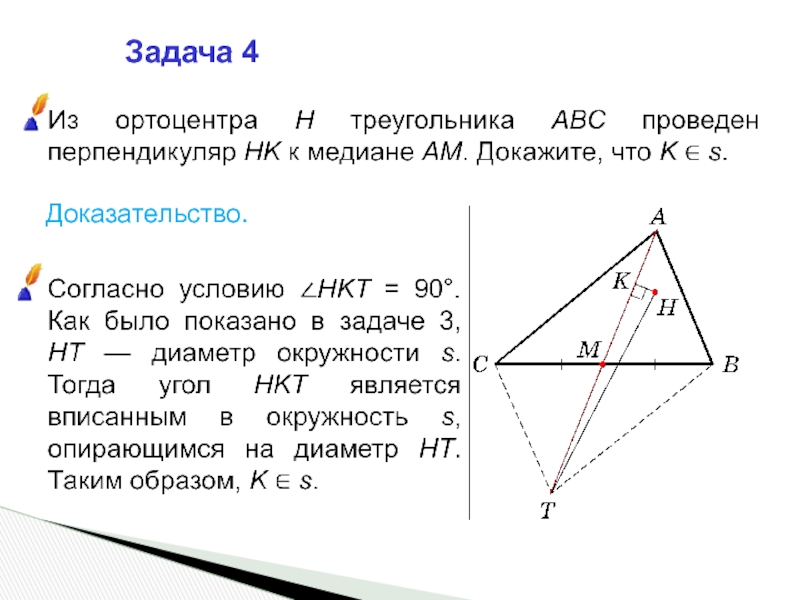
- 9. Задача 4 Доказательство.
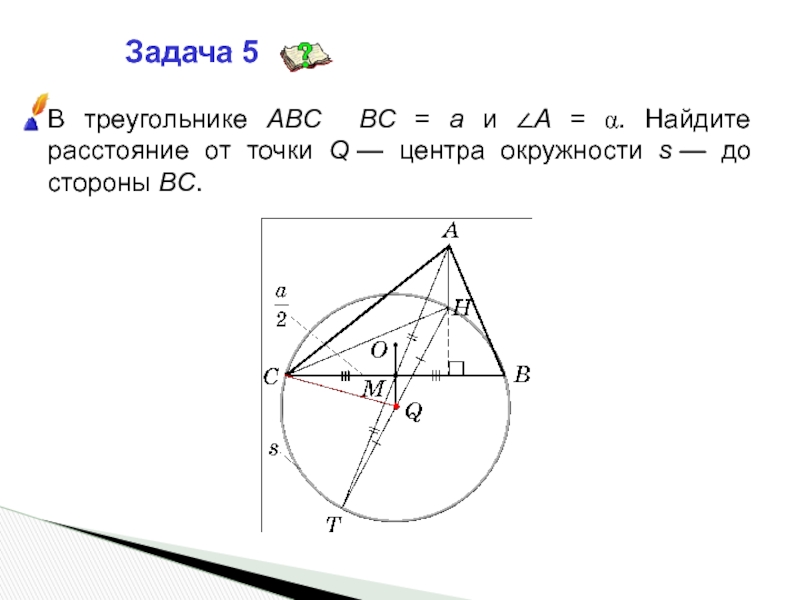
- 10. Задача 5В треугольнике ABC BC = a
- 11. Решение. Очевидно, точка Q — середина отрезка TH —
- 12. Следствие 1Так как QM — средняя линия в
- 13. Задача 6Докажите, что OQHA — параллелограмм.Доказательство. Из задачи
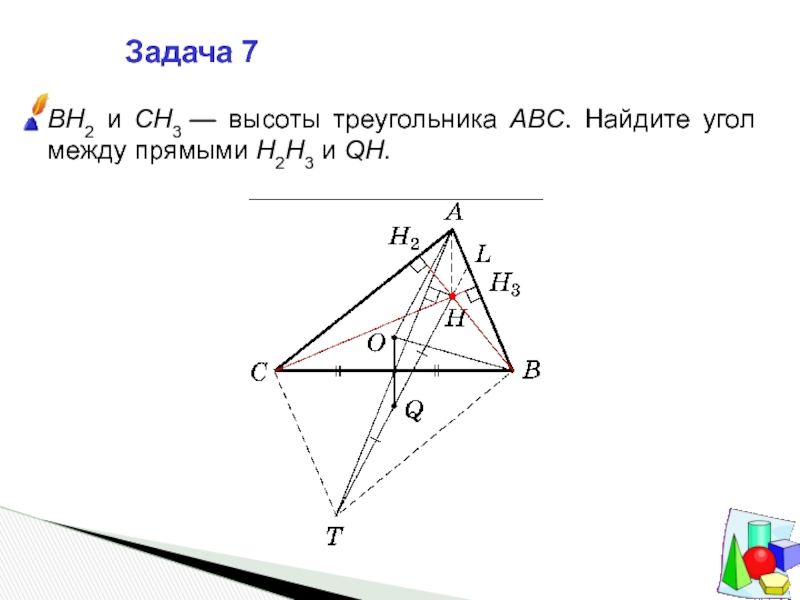
- 14. Задача 7BH2 и CH3 — высоты треугольника ABC. Найдите угол между прямыми H2H3 и QH.
- 15. Решение. ∠AOB = 2∠C — центральный угол окружности
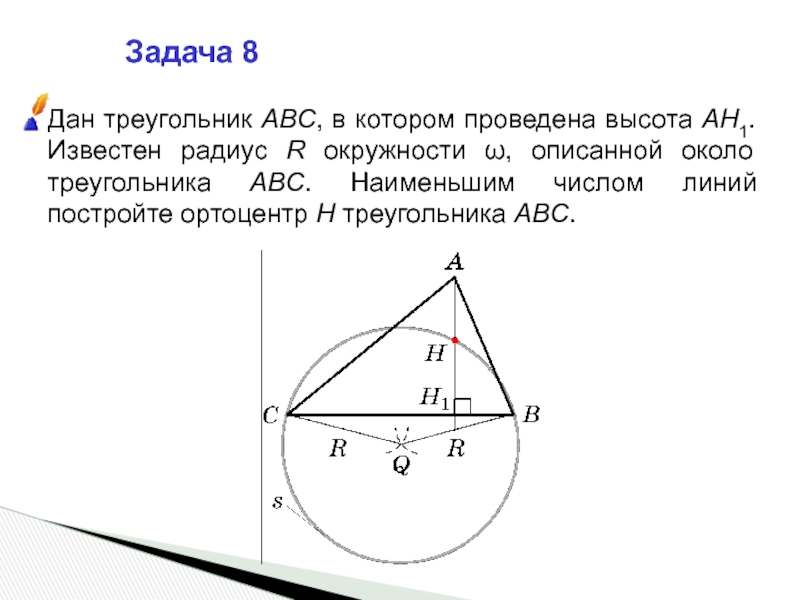
- 16. Задача 8Дан треугольник ABC, в котором проведена
- 17. Решение. Так как Rs = Rω =
- 18. Задача 9Докажите, что прямая AQ является прямой
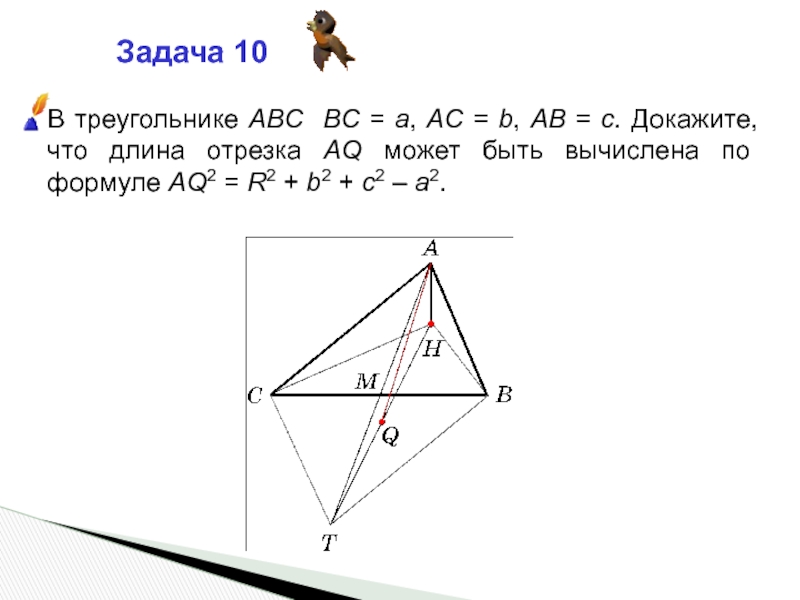
- 19. Задача 10В треугольнике ABC BC = a,
- 20. Доказательство. Способ IПо формуле медианы для треугольника
- 21. Доказательство. Способ IIДля треугольника ABC известна формула:
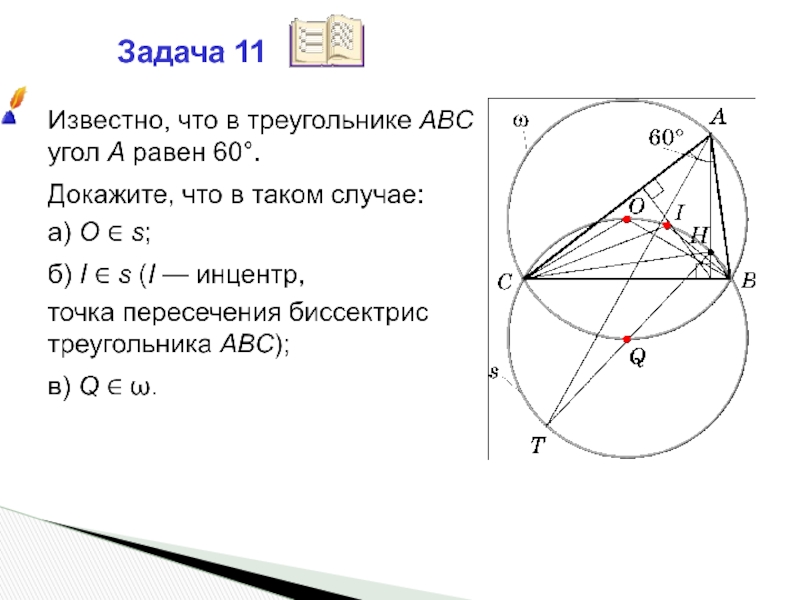
- 22. Задача 11
- 23. а) Так как ∠BOC = 2 ∠A
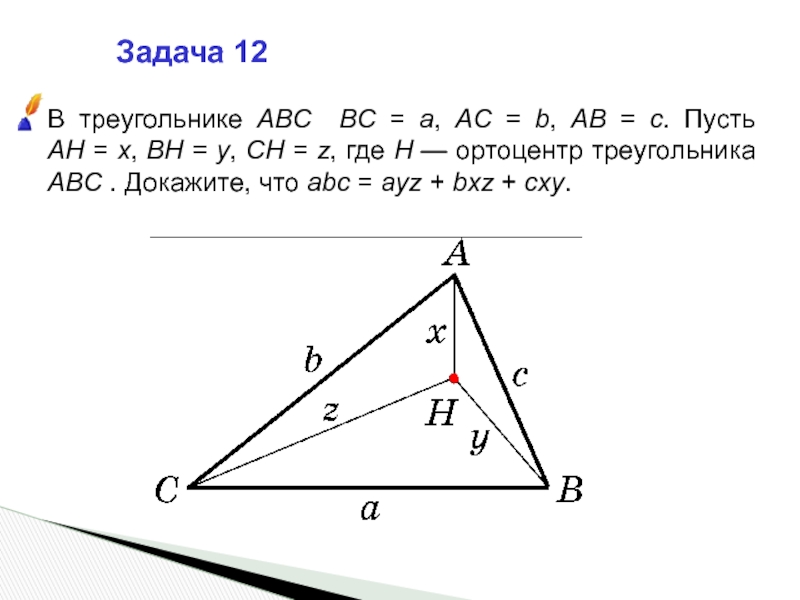
- 24. Задача 12В треугольнике ABC BC = a,
- 25. Доказательство. Воспользуемся леммой Rω = Rs =
- 26. Задача 13Пусть Q1, Q2, Q3 — соответственно центры
- 27. https://yandex.ru/images/search?p=4&text=%D0%B0%D0%BD%D0%B8%D0%BC%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%BD%D0%B0%D1%8F%20%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0http://revolt33.narod.ru/matem/Bereg_site/bereg_3.htmlhttp://methmath.ru/krokr.htmlСПИСОК ЛИТЕРАТУРЫ.
- 28. СПАСИБО ЗА ВНИМАНИЕ
ЛЕММАПусть H — ортоцентр (точка пересечения высот) треугольника ABC. Тогда описанные окружности треугольников ABC, BHC, AHC и AHB равны между собой.
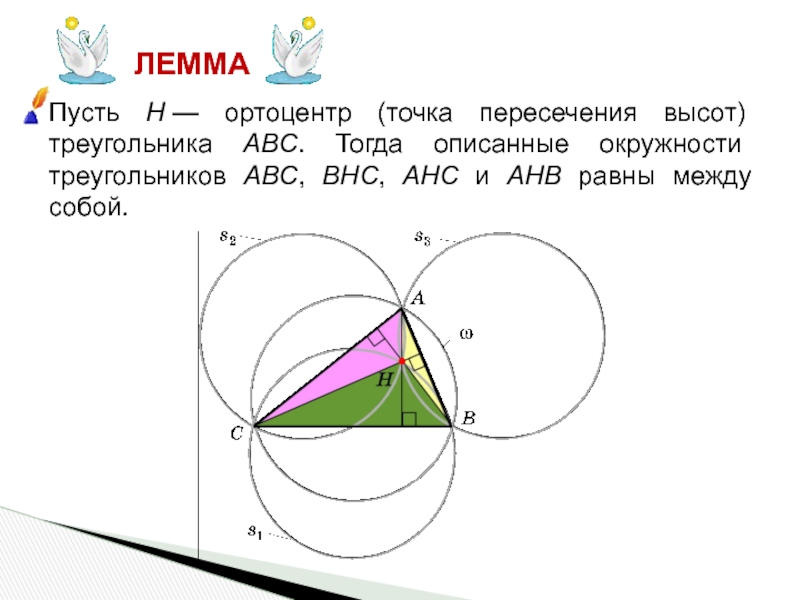
Слайд 2ЛЕММА
Пусть H — ортоцентр (точка пересечения высот) треугольника ABC. Тогда описанные окружности
треугольников ABC, BHC, AHC и AHB равны между собой.
Слайд 4Задача 1
Бывает ли, что окружности ω и s совпадают?
Решение.
Бывает. Если
треугольник ABC — прямоугольный (∠A = 90°), то вершина A является ортоцентром в треугольнике ABC, то есть точки A и H совпадают. В этом случае ω и s — одна и та же окружность.
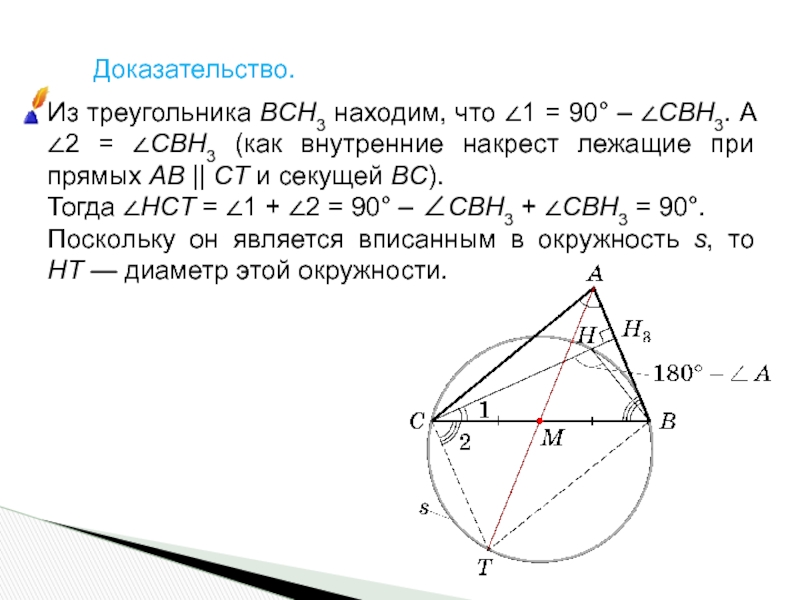
Слайд 8Доказательство.
Из треугольника BCH3 находим, что ∠1 = 90° – ∠CBH3.
А ∠2 = ∠CBH3 (как внутренние накрест лежащие при прямых AB || CT и секущей BC).
Тогда ∠HCT = ∠1 + ∠2 = 90° – ∠CBH3 + ∠CBH3 = 90°.
Поскольку он является вписанным в окружность s, то HT — диаметр этой окружности.
Тогда ∠HCT = ∠1 + ∠2 = 90° – ∠CBH3 + ∠CBH3 = 90°.
Поскольку он является вписанным в окружность s, то HT — диаметр этой окружности.
Слайд 10Задача 5
В треугольнике ABC BC = a и ∠A = α.
Найдите расстояние от точки Q — центра окружности s — до стороны BC.
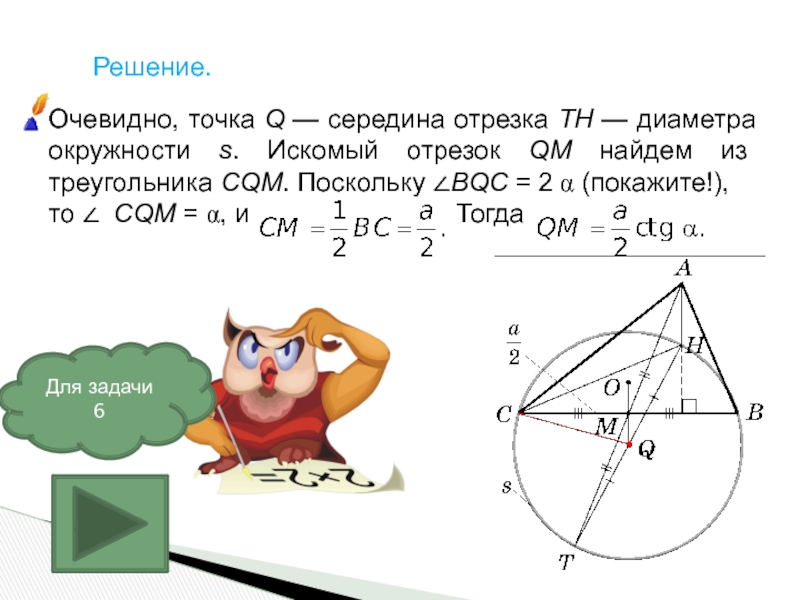
Слайд 11Решение.
Очевидно, точка Q — середина отрезка TH — диаметра окружности s. Искомый
отрезок QM найдем из треугольника CQM. Поскольку ∠BQC = 2 α (покажите!),
то ∠ CQM = α, и Тогда
то ∠ CQM = α, и Тогда
Для задачи 6
Слайд 12Следствие 1
Так как QM — средняя линия в треугольнике AHT, то AH
= a ctg α или, в общем случае, AH = a | ctg α |.
Следствие 2
Так как то точки O (центр описанной
окружности треугольника ABC) и Q симметричны относительно стороны BC.
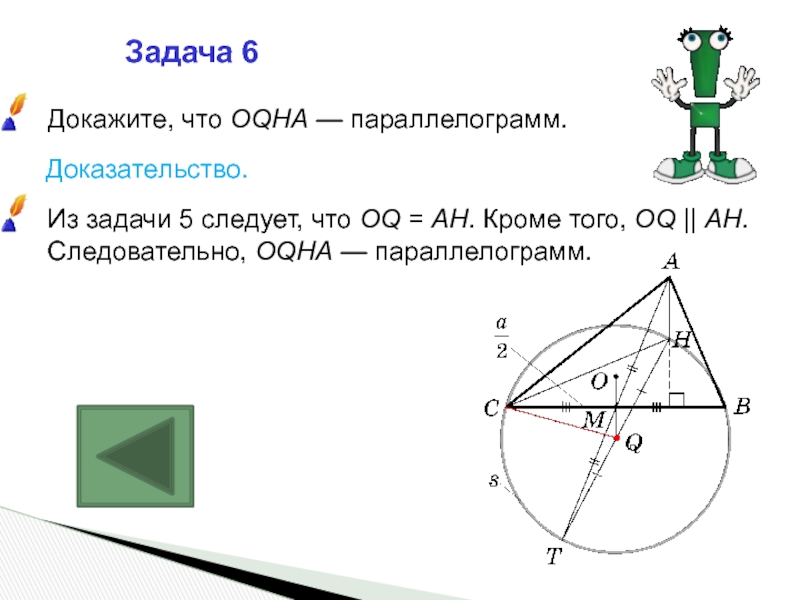
Слайд 13Задача 6
Докажите, что OQHA — параллелограмм.
Доказательство.
Из задачи 5 следует, что OQ
= AH. Кроме того, OQ || AH. Следовательно, OQHA — параллелограмм.
Слайд 15Решение.
∠AOB = 2∠C — центральный угол окружности ω, описанной около треугольника
ABC. Тогда
Пусть L = QH ∩ AB. Очевидно, ∠HLH3 = 90° – ∠C (QH || OA). В то же время ∠BH3H2 = 180° – ∠C, так как точки B, H3, H2, C лежат на одной окружности, в которой BC — диаметр (покажите!).
Тогда смежный с ним ∠LH3H2 = ∠C, значит, прямые H2H3 и QH перпендикулярны.
Пусть L = QH ∩ AB. Очевидно, ∠HLH3 = 90° – ∠C (QH || OA). В то же время ∠BH3H2 = 180° – ∠C, так как точки B, H3, H2, C лежат на одной окружности, в которой BC — диаметр (покажите!).
Тогда смежный с ним ∠LH3H2 = ∠C, значит, прямые H2H3 и QH перпендикулярны.
Слайд 16Задача 8
Дан треугольник ABC, в котором проведена высота AH1. Известен радиус
R окружности ω, описанной около треугольника ABC. Наименьшим числом линий постройте ортоцентр H треугольника ABC.
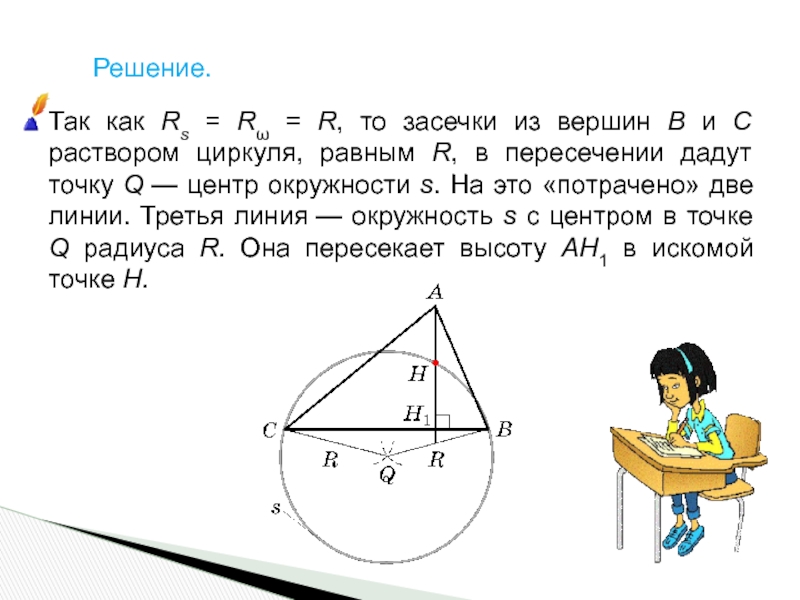
Слайд 17Решение.
Так как Rs = Rω = R, то засечки из
вершин B и C раствором циркуля, равным R, в пересечении дадут точку Q — центр окружности s. На это «потрачено» две линии. Третья линия — окружность s с центром в точке Q радиуса R. Она пересекает высоту AH1 в искомой точке H.
Слайд 18Задача 9
Докажите, что прямая AQ является прямой Эйлера для треугольника BHC.
Доказательство.
Действительно, вершина A является ортоцентром в треугольнике BHC. Точка Q — центр описанной окружности s этого треугольника. Так как прямая Эйлера проходит через центр описанной окружности треугольника и его ортоцентр, то AQ — именно такая прямая для треугольника BHC.
Слайд 19Задача 10
В треугольнике ABC BC = a, AC = b, AB
= c. Докажите, что длина отрезка AQ может быть вычислена по формуле AQ2 = R2 + b2 + c2 – a2.
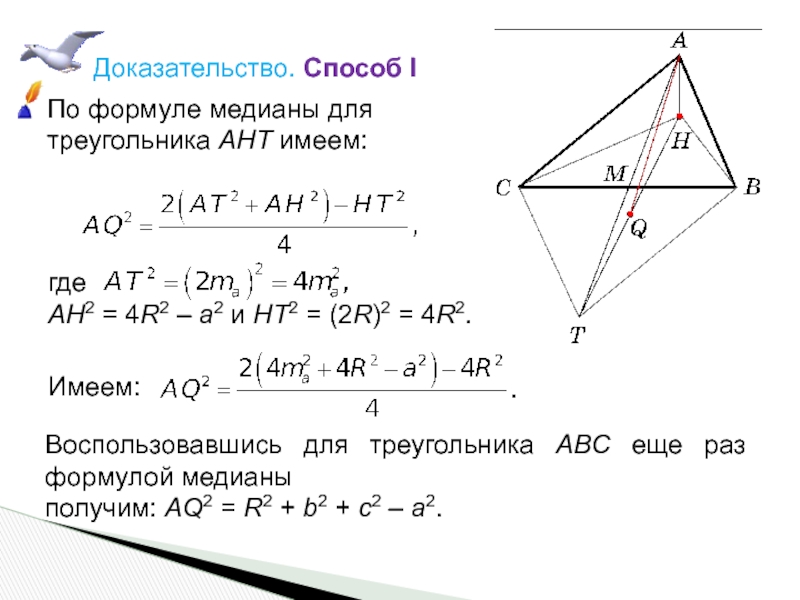
Слайд 20Доказательство. Способ I
По формуле медианы для
треугольника AHT имеем:
где
AH2 = 4R2 – a2 и HT2 = (2R)2 = 4R2.
Имеем:
Воспользовавшись для треугольника ABC еще раз формулой медианы
получим: AQ2 = R2 + b2 + c2 – a2.
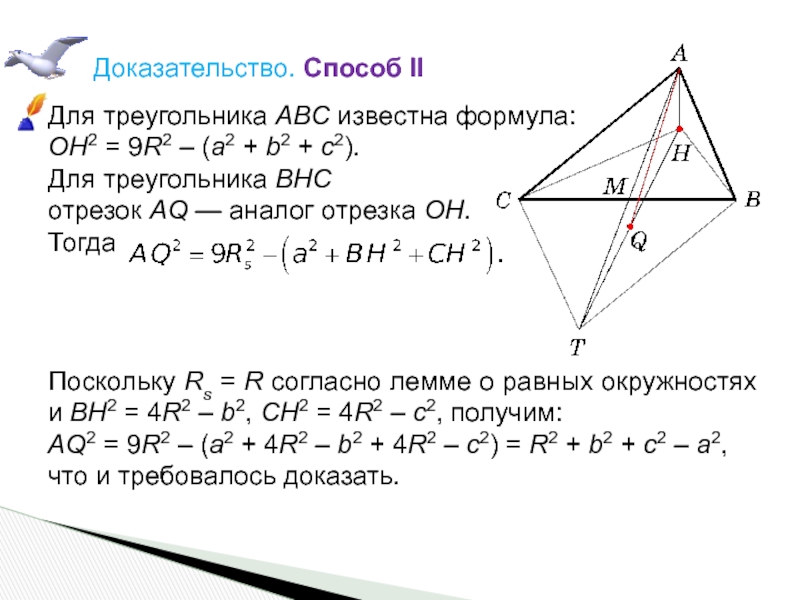
Слайд 21Доказательство. Способ II
Для треугольника ABC известна формула:
OH2 = 9R2 –
(a2 + b2 + c2).
Для треугольника BHC
отрезок AQ — аналог отрезка OH.
Тогда
Для треугольника BHC
отрезок AQ — аналог отрезка OH.
Тогда
Поскольку Rs = R согласно лемме о равных окружностях и BH2 = 4R2 – b2, CH2 = 4R2 – c2, получим:
AQ2 = 9R2 – (a2 + 4R2 – b2 + 4R2 – c2) = R2 + b2 + c2 – a2,
что и требовалось доказать.
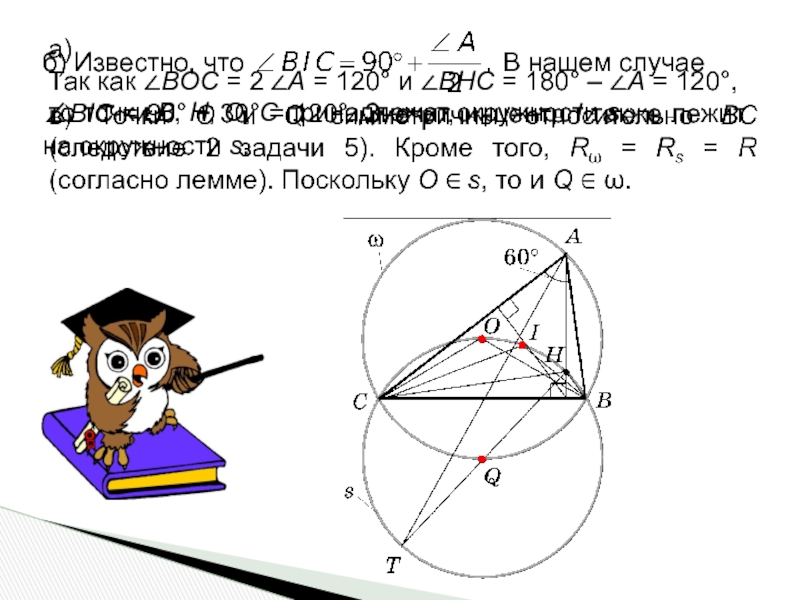
Слайд 23а)
Так как ∠BOC = 2 ∠A = 120° и ∠BHC
= 180° – ∠A = 120°,
то точки B, H, O, C принадлежат окружности s.
то точки B, H, O, C принадлежат окружности s.
б) Известно, что В нашем случае
∠BIC = 90° + 30° = 120°. Значит, инцентр I также лежит на окружности s.
Слайд 24Задача 12
В треугольнике ABC BC = a, AC = b, AB
= c. Пусть AH = x, BH = y, CH = z, где H — ортоцентр треугольника ABC . Докажите, что abc = ayz + bxz + cxy.
Слайд 25Доказательство.
Воспользуемся леммой Rω = Rs = R, формулой
и тем,
что S = SABC = SBHC + SAHC + SAHB.
Нам требуется доказать, что
4SR = 4SBHC · R + 4SAHC · R + 4RAHB · R
или
S = SBHC + SAHC + SAHB,
что верно.
Нам требуется доказать, что
4SR = 4SBHC · R + 4SAHC · R + 4RAHB · R
или
S = SBHC + SAHC + SAHB,
что верно.
Слайд 26Задача 13
Пусть Q1, Q2, Q3 — соответственно центры окружностей s1, s2, s3,
описанных около треугольников BHC, AHC, AHB. Докажите, что AQ1, BQ2 и CQ3 пересекаются в одной точке.
Доказательство.
Мы уже показали, что OQHA — параллелограмм (см. задачу 6). Тогда AQ и OH пересекаются, например, в точке E, где E — середина OH. Итак, AQ (в нашей задаче AQ1) проходит через точку E. Аналогично, каждый из отрезков BQ2 и CQ3 делит OH пополам. Таким образом, все они проходят через точку E — середину OH.
Слайд 27https://yandex.ru/images/search?p=4&text=%D0%B0%D0%BD%D0%B8%D0%BC%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%BD%D0%B0%D1%8F%20%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0
http://revolt33.narod.ru/matem/Bereg_site/bereg_3.html
http://methmath.ru/krokr.html
СПИСОК ЛИТЕРАТУРЫ.
