МКОУ СОШ №6 им. З.Джибилова г.Беслана
г.Беслан, Ленина, 14
3 44 75, 8 928 065 1848
Mrita_4@list.ru
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике К истории числа пи
Содержание
- 1. Презентация по математике К истории числа пи
- 2. Цели и задачиПредметные: формировать умение
- 3. К истории числа
- 4. Открывателями числа можно считать людей доисторического времени,
- 5. Египтяне почти за две тысячи лет до
- 6. Изучением числа П занимались многие математики
- 7. Первый вопрос при этом возникает о
- 8. Из древнеегипетских и вавилонских источников известно, что
- 9. Использование найденного Архимедом значения 3,14 многие годы
- 10. В средние века математики добивались более точности
- 11. В настоящее время с помощью компьютера можно
- 12. Впервые обозначением этого числа греческой буквой воспользовался
- 13. Дополнительные факты.-Неофициальный праздник «День числа П »
- 14. Еще некоторые факты14 марта в день
- 15. Мы тоже провели свои эксперименты и на практике доказали, что П=3,14….
- 16. Слайд 16
- 17. Слайд 17
- 18. Список использованных ресурсов1.Математика 6,А.Г.Мерзляк, В.Б.Полонский, М.С.Якир;Москва,2014г2.Газета
Цели и задачиПредметные: формировать умение выполнять геометрические построения с помощью циркуля.Личностные: развивать познавательный интерес к математике, развивать интерес к исследовательской деятельности, формировать умение представлять результат своей деятельности, формировать умение работать в коллективе и находить
Слайд 1История математики
Тема: «К истории числа П»
Тумарова Виктория Черменовна
Рукаводитель: Дзуцева Зинаида
Заурбековна
Слайд 2
Цели и задачи
Предметные: формировать умение выполнять геометрические построения с
помощью циркуля.
Личностные: развивать познавательный интерес к математике, развивать интерес к исследовательской деятельности, формировать умение представлять результат своей деятельности, формировать умение работать в коллективе и находить согласованные решения.
Метапредметные: развивать умение формулировать, ставить для себя новые задачи в учебе и познавательной, расширить мотивы и интересы своей познавательной деятельности, формировать умение использовать приобретенные знания в проектной деятельности.
Личностные: развивать познавательный интерес к математике, развивать интерес к исследовательской деятельности, формировать умение представлять результат своей деятельности, формировать умение работать в коллективе и находить согласованные решения.
Метапредметные: развивать умение формулировать, ставить для себя новые задачи в учебе и познавательной, расширить мотивы и интересы своей познавательной деятельности, формировать умение использовать приобретенные знания в проектной деятельности.
Слайд 4 Открывателями числа можно считать людей доисторического времени, которые при плетении корзин
заметили, что для того, чтобы получить корзину нужного диаметра, необходимо брать прутья в три раза длиннее его. Найдены таблички из обожженной глины в Месопотамии, на которых зафиксирован данный факт.
Слайд 5Египтяне почти за две тысячи лет до нашей эры заметили, что
диаметр окружности не содержится точно три раза в ее длине. С того времени начинается изучение числа П, которое продолжается и до наших дней.
Слайд 6 Изучением числа П занимались многие математики всех времен и народов.
Столь внимательное отношение к числу неслучайно. Это число играет важную роль в математике, физике, астрономии, технике и других науках, многих практических расчетах. Действительно, без знаний о числе П нельзя вычислить длину окружности, площадь круга, площади поверхностей и объемы круглых тел, выполнить многие расчеты в электротехнике и радиотехнике, астрономии и космонавтике. Можно с полной уверенностью утверждать, что по характеру и полноте знаний о числе возможно судить о научно-техническом уровне развития данного общества.
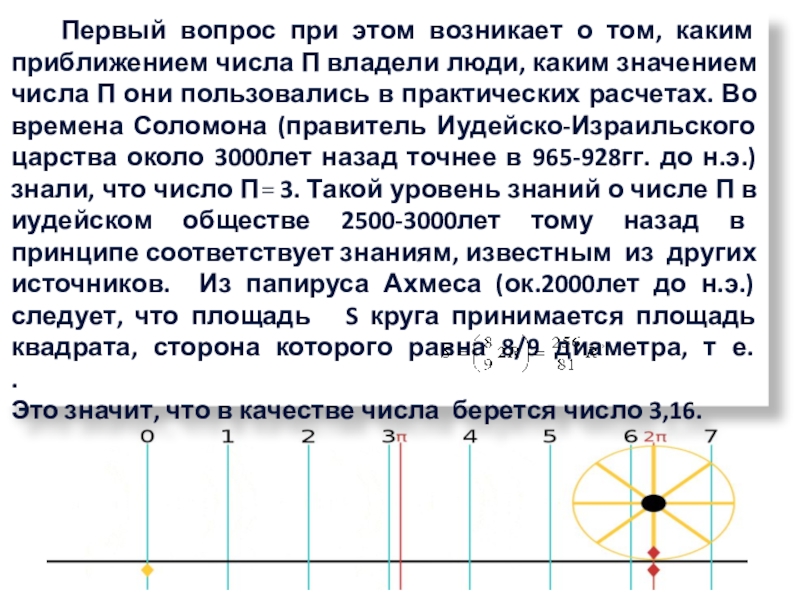
Слайд 7 Первый вопрос при этом возникает о том, каким приближением числа
П владели люди, каким значением числа П они пользовались в практических расчетах. Во времена Соломона (правитель Иудейско-Израильского царства около 3000лет назад точнее в 965-928гг. до н.э.) знали, что число П= 3. Такой уровень знаний о числе П в иудейском обществе 2500-3000лет тому назад в принципе соответствует знаниям, известным из других источников. Из папируса Ахмеса (ок.2000лет до н.э.) следует, что площадь S круга принимается площадь квадрата, сторона которого равна 8/9 диаметра, т е. .
Это значит, что в качестве числа берется число 3,16.
Это значит, что в качестве числа берется число 3,16.
Слайд 8 Из древнеегипетских и вавилонских источников известно, что потребности того времени вполне
удовлетворялись значением числа, равным 3. Позже римляне принимали значение П, равное 3,12.
В истории математики считается, что первое вычисление на основе строгих теоретических рассуждений было выполнено выдающимся математиком древности Архимедом (287-212гг.до н.э.). В своем труде «Об измерении, круга» он доказал , что
В истории математики считается, что первое вычисление на основе строгих теоретических рассуждений было выполнено выдающимся математиком древности Архимедом (287-212гг.до н.э.). В своем труде «Об измерении, круга» он доказал , что
Слайд 9 Использование найденного Архимедом значения 3,14 многие годы вполне удовлетворяло практические расчеты.
Примерно
такое же представление о числе П характерно для математиков древней Азии.
В индийских «сутрах» (7-5вв. до н. э.) принимается значение числа П , равное 3,008.
Значительно позже Ариабхатта(5в) и Бхаскара(12в) в качестве брали значение, т.е.3,1416… Брахмагупта(6-7в), Магавира(9в) и Сриддхара(11в) значение П т.е. 3,162…; астроном Ван Фань(229-267гг.) считал, что, т.е.3,155…, Цзу Чун-чжи(428-499г) «точным» значением.
В индийских «сутрах» (7-5вв. до н. э.) принимается значение числа П , равное 3,008.
Значительно позже Ариабхатта(5в) и Бхаскара(12в) в качестве брали значение, т.е.3,1416… Брахмагупта(6-7в), Магавира(9в) и Сриддхара(11в) значение П т.е. 3,162…; астроном Ван Фань(229-267гг.) считал, что, т.е.3,155…, Цзу Чун-чжи(428-499г) «точным» значением.
Слайд 10 В средние века математики добивались более точности в вычислении числа, применяя
метод Архимеда, т.е. вычисляя длину окружности с помощью периметров вписанных в нее или описанных около нее многоугольников. Так ал-Каши в 1424 году в книге «Об измерении окружности» нашел 16 верных знаков числа, бельгиец А.Ван Ромен в 16 веке нашел 17 верных десятичных знаков, голландец Лудольф Ван Цейлен- не сделел великих открытий. Но он вошел в историю благодаря большому терпению и выдержке в своих научных изысканиях. Лудольф ван Цейлен сумел получить 35 верных десятичных знаков для числа. В его честь число было названо современниками «Лудольфово число». Согласно завещанию ван Цейлен, на его надгробии было высечено найденное им значение числа. В течение 18-20 веков Л. Эйлер, У Джоне, В.Шенкс, Ферпоссом, Ренг постепенно увеличивали точность значений числа и нашли его значение с огромной точностью (808 знаков!). Но они уже пользовались методами высшей математики.
Слайд 11 В настоящее время с помощью компьютера можно найти значение сколь угодно
«далекого» десятичного знака числа за сравнительно небольшой промежуток времени.
- иррациональное число, т.е. его значение не может быть точно выражено в виде дроби, где m и n целые числа. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим.
также не может представлено как конечная последовательность алгебраических операций над целыми числами.
-трансцендентное число, это означает, что оно не может быть корнем какого–либо многочлена с целыми коэффициентами.
- иррациональное число, т.е. его значение не может быть точно выражено в виде дроби, где m и n целые числа. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим.
также не может представлено как конечная последовательность алгебраических операций над целыми числами.
-трансцендентное число, это означает, что оно не может быть корнем какого–либо многочлена с целыми коэффициентами.
Слайд 12 Впервые обозначением этого числа греческой буквой воспользовался британский математик Джонс(1700),а общепринятым
оно стало после работ Леонарда Эйлера в 1737 году. Это обозначение происходит от начальной буквы греческого слова периферия, что означает окружность.
История числа шла параллельно с развитием всей математики. Некоторые авторы разделяют весь процесс на три периода: древний период, в течение которого изучалось с позиции геометрии, классическая эра, последовавшая за развитием математического анализа в Европе в 12 веке, и эра цифровых компьютеров.
История числа шла параллельно с развитием всей математики. Некоторые авторы разделяют весь процесс на три периода: древний период, в течение которого изучалось с позиции геометрии, классическая эра, последовавшая за развитием математического анализа в Европе в 12 веке, и эра цифровых компьютеров.
Слайд 13Дополнительные факты.
-Неофициальный праздник «День числа П » отмечается 14 марта, которое
в американском формате дат(месяц/день) записывается как 3.14, что соответствует приближенному значению числа П .
-Еще одной датой, связанной с числом П является 2 июля, которое называется «Днем приближенного числа П»,так как в европейском формате дат этот день записывается как.
-17 июня 2009 года украинский нейрохирург, доктор медицинских наук, профессор Андрей Слюсарчук установил мировой рекорд запомнив 30 миллионов знаков числа .
-По состоянию на 2010 год вычислено 5 триллионов знаков после запятой.
-По состоянию на 2011 год вычислено 10 триллионов знаков после запятой.
-По состоянию на 2014 год вычислено 13,3 триллионов знаков после запятой.
-Еще одной датой, связанной с числом П является 2 июля, которое называется «Днем приближенного числа П»,так как в европейском формате дат этот день записывается как.
-17 июня 2009 года украинский нейрохирург, доктор медицинских наук, профессор Андрей Слюсарчук установил мировой рекорд запомнив 30 миллионов знаков числа .
-По состоянию на 2010 год вычислено 5 триллионов знаков после запятой.
-По состоянию на 2011 год вычислено 10 триллионов знаков после запятой.
-По состоянию на 2014 год вычислено 13,3 триллионов знаков после запятой.
Слайд 14 Еще некоторые факты
14 марта в день числа родился Альберт Эйнштейн.
Существует
художественный фильм, названный в честь числа.
Число очень полюбилось не только математикам, но и скульпторам. Иначе, как же объяснить такое количество памятников числу по всему миру.
-Установлен памятник числу на ступенях перед зданием Музея искусств в Сиэтле.
-На южном побережье Крыма близ поселка Кацивели.
-В городе Озерске Челябинской области. Этот памятник появился в результате работы Первого симпозиума скульптора «Атомное сердце» в 2011году.
-В Черногории, в городе Будва находится еще один памятник.
-В Волгограде.
-Штат Нью-Джерси, США, в Парке скульптур.
-И напоследок еще один памятник в городе Тольятти
Число очень полюбилось не только математикам, но и скульпторам. Иначе, как же объяснить такое количество памятников числу по всему миру.
-Установлен памятник числу на ступенях перед зданием Музея искусств в Сиэтле.
-На южном побережье Крыма близ поселка Кацивели.
-В городе Озерске Челябинской области. Этот памятник появился в результате работы Первого симпозиума скульптора «Атомное сердце» в 2011году.
-В Черногории, в городе Будва находится еще один памятник.
-В Волгограде.
-Штат Нью-Джерси, США, в Парке скульптур.
-И напоследок еще один памятник в городе Тольятти
Слайд 18
Список использованных ресурсов
1.Математика 6,
А.Г.Мерзляк, В.Б.Полонский, М.С.Якир;Москва,2014г
2.Газета «Математика в школе»
3.Большая математическая
энциклопедия для школьников и студентов,Москва,2004г. 4.ttp://mersinlihoca.com/pluginfile.php/1256/mod_label/intro/kZXwODP.gif