- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Графики тригонометрии
Содержание
- 1. Презентация по математике Графики тригонометрии
- 2. « … математика … выявляет порядок, симметрию и определенность, а это важнейшие виды прекрасного».Аристотель
- 3. ху01-1π2π- π-2 π- Π 2 Π 2-3Π 23Π 2y = sin x
- 4. ООФ (- ∞; + ∞)Четность нечетная
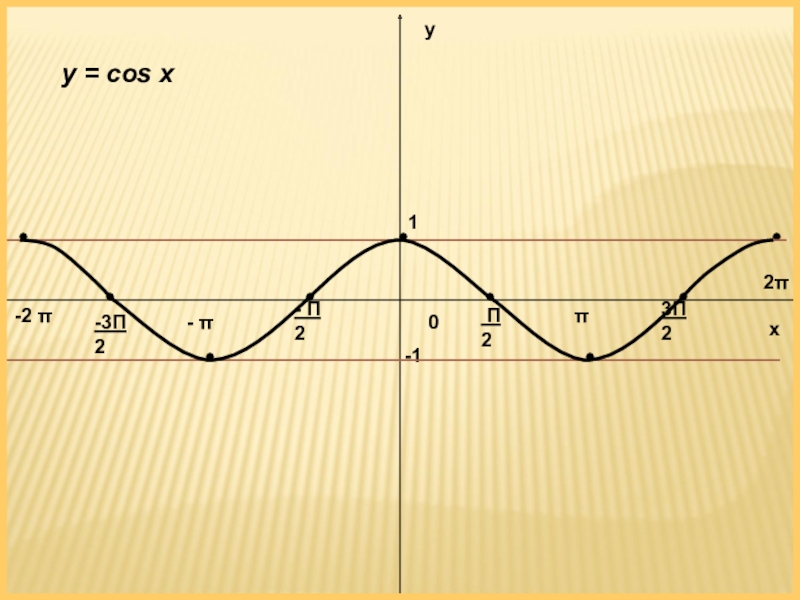
- 5. ху01-1π2π- π-2 π- Π 2 Π 2-3Π 23Π 2y = cos x
- 6. СВОЙСТВА ФУНКЦИИ y = cos xООФ
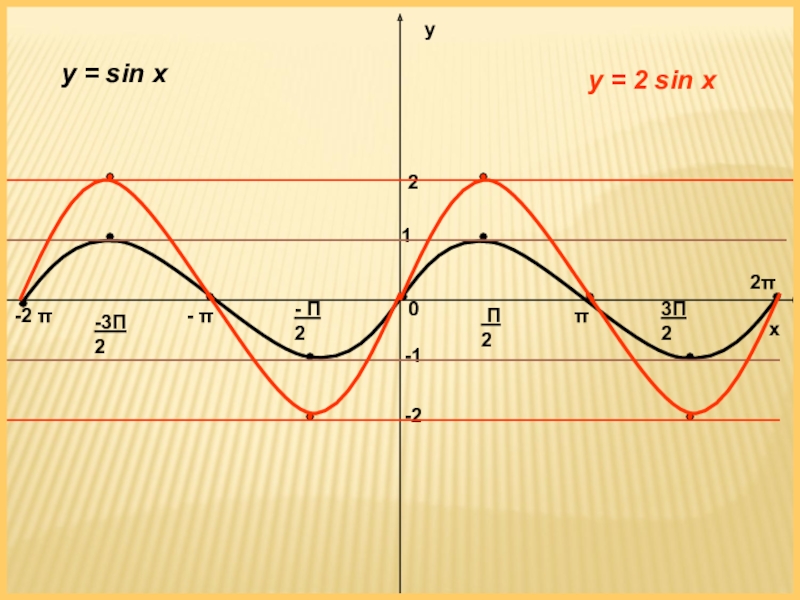
- 7. y = 2 sin xy = 3
- 8. ху01-1π2π- π-2 π- Π 2 Π 2-3Π 23Π 2y = sin xy = 2 sin x2-2
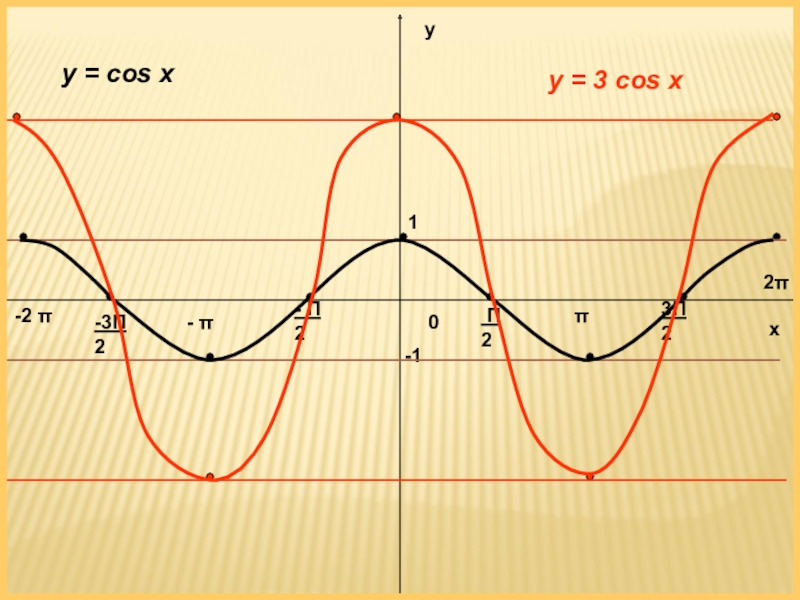
- 9. ху01-1π2π- π-2 π- Π 2 Π 2-3Π 23Π 2y = cos xy = 3 cos x
- 10. y= sin xy= 0, 5 sin xy=
- 11. Построение графика функции y=k sin x, y=k
- 12. Постройте в одной системе координат графики функций
- 13. КАК ПОСТРОИТЬ ГРАФИК ФУНКЦИИ y = k
- 14. ху01-1π2π- π-2 π- Π 2 Π 2-3Π
- 15. ху01-1π2π- π-2 π- Π 2 Π 2-3Π
- 16. ху01-1π2π- π-2 π- Π 2 Π 2-3Π
- 17. Постройте график функции
- 18. Постройте график функции
- 19. Найдите наибольшее и наименьшее значение функции y
- 20. ху-2 π-3Π 2- π- Π 20Π 2π3Π
- 21. Определите, сколько решений имеет система уравнений
- 22. ху-2 π-3Π 2- π- Π 20Π 2π3Π
- 23. Какую проблему мы сегодня решали?Как мы строим
Слайд 1
Интегрированный урок
по математике
в 10 классе по теме
«ПРЕОБРАЗОВАНИЯ ГРАФИКОВ
ТРИГОНОМЕТРИЧЕСКИХ
Слайд 2
« … математика … выявляет порядок, симметрию и определенность, а это
Аристотель
Слайд 4
ООФ (- ∞; + ∞)
Четность нечетная
Монотонность: возрастает [ - π/2 + 2 π к; π/2 + 2 π к]; убывает [ π/2 + 2 π к; 3π/2 + 2 π к]
Ограниченность: сверху у = 1, снизу у = -1
Наибольшее и наименьшее значение у наиб.= 1; у наим.= -1
Непрерывность: непрерывна
ОЗФ [-1; 1 ]
Периодичность: периодическая с периодом 2 π
СВОЙСТВА ФУНКЦИИ
y = sin x
Слайд 6
СВОЙСТВА ФУНКЦИИ
y = cos x
ООФ (- ∞; + ∞)
Четность
Монотонность: возрастает [ π + 2 π к; 2π + 2 π к]; убывает [ 0 + 2 π к; π + 2 π к]
Ограниченность: сверху у = 1, снизу у = -1
Наибольшее и наименьшее значение у наиб.= 1; у наим.= -1
Непрерывность: непрерывна
ОЗФ [-1; 1 ]
Периодичность: периодическая с периодом 2 π
Слайд 7
y = 2 sin x
y = 3 cos x
ООФ (-
Четность нечетная sin (-x) = - sin x
Монотонность: возрастает [ - π/2 + 2 π к; π/2 + 2 π к]; убывает [ π/2 + 2 π к; 3π/2 + 2 π к]
Ограниченность: сверху у = 2, снизу у = -2
Наибольшее и наименьшее значение у наиб.= 2; у наим.= -2
Непрерывность: непрерывна
ОЗФ [-2; 2 ]
Периодичность: периодическая с периодом 2 π
ООФ (- ∞; + ∞)
Четность четная cos (-x) = cos x
Монотонность: возрастает [ π + 2 π к; 2π + 2 π к]; убывает [ 0 + 2 π к; π + 2 π к]
Ограниченность: сверху у = 3, снизу у = -3
Наибольшее и наименьшее значение у наиб.= 3; у наим.= -3
Непрерывность: непрерывна
ОЗФ [-3; 3 ]
Периодичность: периодическая с периодом 2 π
Слайд 10
y= sin x
y= 0, 5 sin x
y= 0,25 sin x
y= ¾
y= 4 sin x
y= 2,5 sin x
y=1,5 sin x
y= - sin x
y= -2 sin x
y= -1,5 sin x
y= к sin x
y= cos x
y= 0, 5 cos x
y= 0,25 cos x
y= ¾ cos x
y= 4 cos x
y= 2,5 cos x
y=1,5 cos x
y= - cos x
y= -2 cos x
y= -1,5 cos x
y= к cos x
Слайд 11
Построение графика функции y=k sin x, y=k cos x,
если известен график
у = sin x, y = cos x
Слайд 12Постройте в одной системе координат графики функций y= sin x;
Выводы: Постройте в одной системе координат графики функций y= sin x; y= 4 sin x; y= 2,5 sin x; y=1,5 sin x. Выводы: Постройте в одной системе координат графики функций y= sin x; y= - sin x; y= -2 sin x; y= -1,5 sin x. Выводы:
Если 0
Если к>1 , то график функции y = к sin x получается из графика функции y = sin x растяжением от оси х с коэффициентом к.
Чтобы построить графики данных функций нужно: 1) построить график функции y= sin x; 2) оставить без изменения точки пересечения с осями; 3) ординаты остальных точек увеличить в к раз.
Если k<0, то график функции y = к sin x получается из графика функции y = sin x растяжением от оси х с коэффициентом к и симметрией относительно оси х.
Чтобы построить графики данных функций нужно: 1) построить график функции y= sin x; 2) оставить без изменения точки пересечения с осями; 3) ординаты остальных точек увеличить в к раз; 4) выполнить преобразование симметрии относительно оси х.
Слайд 13КАК ПОСТРОИТЬ ГРАФИК ФУНКЦИИ y = k sin x,
если известен
Чтобы построить график функции y = k sin x нужно:
построить график функции y= sin x;
2) оставить без изменения точки пересечения с осями;
3) ординаты остальных точек:
если 0
если k<0 и 0
а затем выполнить преобразование симметрии относительно оси х.
Слайд 14
х
у
0
1
-1
π
2π
- π
-2 π
- Π 2
Π 2
-3Π 2
3Π 2
y = -
№ 230 (г)
№ 235 (г)
№ 235 (б)
y = 3 cos x - 2
y = - 0,5 cos x + 2
Слайд 15
х
у
0
1
-1
π
2π
- π
-2 π
- Π 2
Π 2
-3Π 2
3Π 2
а
б
в
г
2
3
-2
-3
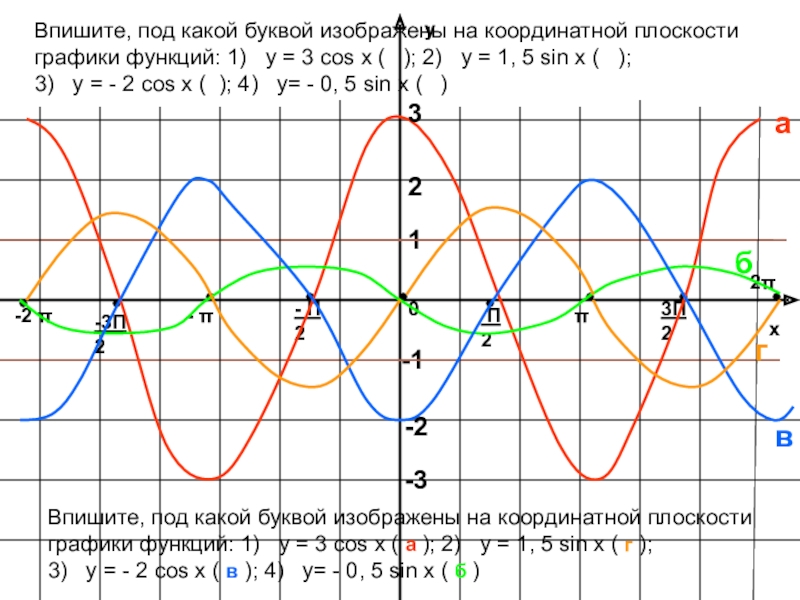
Впишите, под какой
3) y = - 2 cos x ( ); 4) y= - 0, 5 sin x ( )
Впишите, под какой буквой изображены на координатной плоскости графики функций: 1) y = 3 cos x ( а ); 2) y = 1, 5 sin x ( г );
3) y = - 2 cos x ( в ); 4) y= - 0, 5 sin x ( б )
Слайд 16
х
у
0
1
-1
π
2π
- π
-2 π
- Π 2
Π 2
-3Π 2
3Π 2
2
3
-2
-3
1
2
3
4
№2. Запишите функции,
1) y = - sin x ; 2) y = 1,5 cos x; 3) y = 0,5 sin x ; 4) y = 3 cos x
Слайд 18Постройте график функции
F(x) =
2 cos x +3, если x ≥ π/2
х
у
-2 π
-3Π 2
- π
- Π 2
0
Π 2
π
3Π 2
2π
1
2
3
-1
-2
-3
Слайд 19Найдите наибольшее и наименьшее значение функции y = 2 cos x
а) на отрезке [ - π/2; π/2]; б) на интервале ( 0; 3π/2); в) на полуинтервале [ π/3; 3π/2)
Слайд 20х
у
-2 π
-3Π 2
- π
- Π 2
0
Π 2
π
3Π 2
2π
1
2
3
-1
-2
-3
Найдите наибольшее и наименьшее
а) на отрезке [ - π/2; π/2]; б) на интервале ( 0; 3π/2); в) на полуинтервале [ π/3; 3π/2)
Слайд 22
х
у
-2 π
-3Π 2
- π
- Π 2
0
Π 2
π
3Π 2
2π
1
2
3
-1
-2
-3
Определите, сколько решений имеет
y = 2 cos x,
y = - 3 x²
-1
1
Слайд 23
Какую проблему мы сегодня решали?
Как мы строим график вида y =
При выполнении каких заданий мы сегодня использовали построение таких графиков?
АНКЕТА
1. Узнали ли Вы сегодня что-то новое для себя на уроке?
2. Научились ли Вы чему-то новому на уроке?
3. Как Вы оцениваете свою работу на уроке:
Отлично
Хорошо
Удовлетворительно
Плохо
4. Какое Ваше настроение после этого урока:
Отличное
Хорошее
Обычное
Плохое