- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Геометрия масс
Содержание
- 1. Презентация по математике Геометрия масс
- 2. «…Я
- 3. Всякая система, состоящая из конечного числа материальных
- 4. Цель: Изучение и практическое применение барицентрического метода при решении геометрических задач.
- 5. Задачи:Познакомиться с литературой по истории математики.Изучить литературу
- 6. Теорема Архимеда: три медианы
- 7. Доказательство.1)Пусть АВС- произвольный треугольник, АF, ВT
- 8. Пусть АВС - данный треугольник; АА1,ВВ1,СС1- его
- 9. Методы исследования: Поисковый метод с использованием дополнительной
- 10. Задача №1 :Дано: ∆АВС, Кє АВ, N
- 11. Задача №2: Дано:∆ АВС, М є
- 12. Выводы: При
- 13. Заключение: Утверждения и теоремы, доказанные
«…Я счёл нужным написать тебе и…изложить особый метод, при помощи которого ты получишь возможность находить некоторые математические теоремы. Я уверен, что этот метод будет ничуть не менее полезен и для
Слайд 2
«…Я счёл нужным написать тебе
и…изложить особый метод, при помощи которого ты получишь возможность находить некоторые математические теоремы. Я уверен, что этот метод будет ничуть не менее полезен и для доказательства самих теорем».
Архимед
(III в. до н.э )
Слайд 3
Всякая система, состоящая из конечного числа материальных точек, имеет центр масс
и притом единственный.
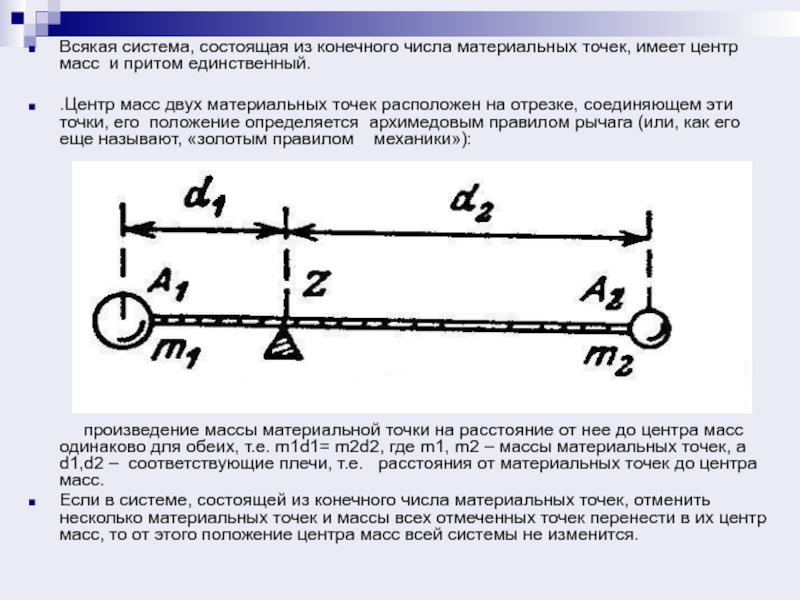
.Центр масс двух материальных точек расположен на отрезке, соединяющем эти точки, его положение определяется архимедовым правилом рычага (или, как его еще называют, «золотым правилом механики»):
произведение массы материальной точки на расстояние от нее до центра масс одинаково для обеих, т.е. m1d1= m2d2, где m1, m2 – массы материальных точек, а d1,d2 – соответствующие плечи, т.е. расстояния от материальных точек до центра масс.
Если в системе, состоящей из конечного числа материальных точек, отменить несколько материальных точек и массы всех отмеченных точек перенести в их центр масс, то от этого положение центра масс всей системы не изменится.
.Центр масс двух материальных точек расположен на отрезке, соединяющем эти точки, его положение определяется архимедовым правилом рычага (или, как его еще называют, «золотым правилом механики»):
произведение массы материальной точки на расстояние от нее до центра масс одинаково для обеих, т.е. m1d1= m2d2, где m1, m2 – массы материальных точек, а d1,d2 – соответствующие плечи, т.е. расстояния от материальных точек до центра масс.
Если в системе, состоящей из конечного числа материальных точек, отменить несколько материальных точек и массы всех отмеченных точек перенести в их центр масс, то от этого положение центра масс всей системы не изменится.
Слайд 4
Цель:
Изучение и практическое применение
барицентрического метода при решении
геометрических задач.
Слайд 5Задачи:
Познакомиться с литературой по истории математики.
Изучить литературу по исследуемой проблеме математического
характера.
Осмыслить свойства центров масс материальных точек.
Показать практическое применение и сравнить и сравнить с традиционным методом решения геометрических задач.
По итогам работы сделать презентацию.
Осмыслить свойства центров масс материальных точек.
Показать практическое применение и сравнить и сравнить с традиционным методом решения геометрических задач.
По итогам работы сделать презентацию.
Слайд 6Теорема Архимеда: три медианы треугольника имеют общую точку, и
каждая из медиан делится этой
точкой в отношении 2:1, считая от вершины.
Слайд 7
Доказательство.
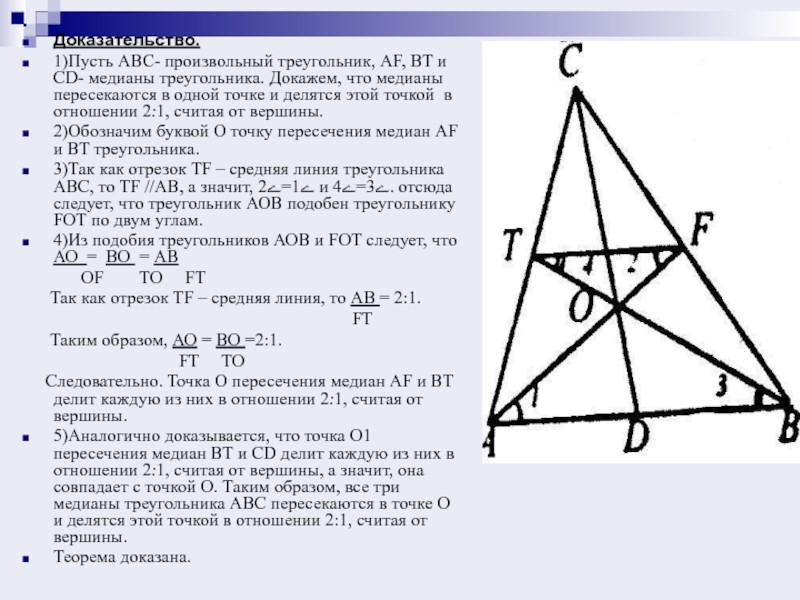
1)Пусть АВС- произвольный треугольник, АF, ВT и СD- медианы треугольника.
Докажем, что медианы пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.
2)Обозначим буквой О точку пересечения медиан АF и ВT треугольника.
3)Так как отрезок TF – средняя линия треугольника АВС, то TF //АВ, а значит, ﮮ1=ﮮ2 и ﮮ3=ﮮ4. отсюда следует, что треугольник АОВ подобен треугольнику FОТ по двум углам.
4)Из подобия треугольников АОВ и FОТ следует, что АО = BO = АВ
ОF ТO FT
Так как отрезок TF – средняя линия, то АВ = 2:1.
FT
Таким образом, АО = ВО =2:1.
FT ТО
Следовательно. Точка О пересечения медиан АF и BT делит каждую из них в отношении 2:1, считая от вершины.
5)Аналогично доказывается, что точка О1 пересечения медиан ВТ и СD делит каждую из них в отношении 2:1, считая от вершины, а значит, она совпадает с точкой О. Таким образом, все три медианы треугольника АВС пересекаются в точке О и делятся этой точкой в отношении 2:1, считая от вершины.
Теорема доказана.
2)Обозначим буквой О точку пересечения медиан АF и ВT треугольника.
3)Так как отрезок TF – средняя линия треугольника АВС, то TF //АВ, а значит, ﮮ1=ﮮ2 и ﮮ3=ﮮ4. отсюда следует, что треугольник АОВ подобен треугольнику FОТ по двум углам.
4)Из подобия треугольников АОВ и FОТ следует, что АО = BO = АВ
ОF ТO FT
Так как отрезок TF – средняя линия, то АВ = 2:1.
FT
Таким образом, АО = ВО =2:1.
FT ТО
Следовательно. Точка О пересечения медиан АF и BT делит каждую из них в отношении 2:1, считая от вершины.
5)Аналогично доказывается, что точка О1 пересечения медиан ВТ и СD делит каждую из них в отношении 2:1, считая от вершины, а значит, она совпадает с точкой О. Таким образом, все три медианы треугольника АВС пересекаются в точке О и делятся этой точкой в отношении 2:1, считая от вершины.
Теорема доказана.
Слайд 8
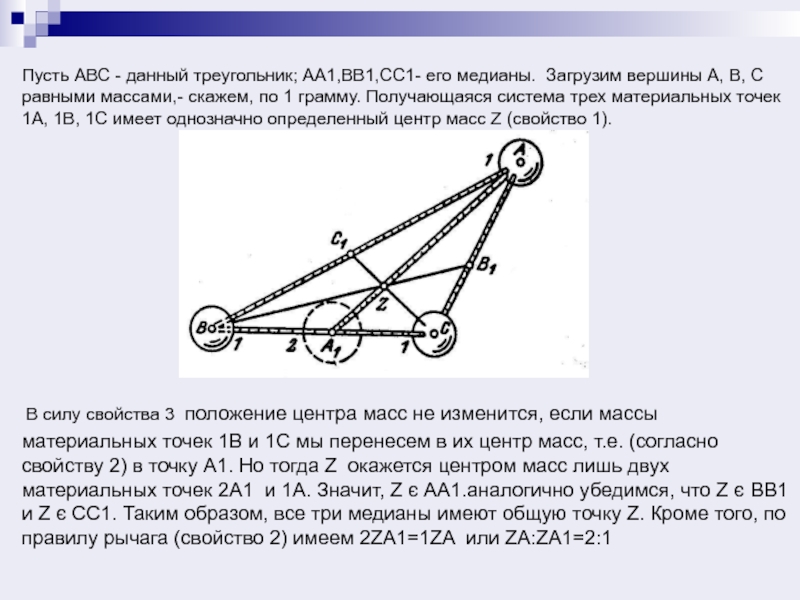
Пусть АВС - данный треугольник; АА1,ВВ1,СС1- его медианы. Загрузим вершины А,
В, С равными массами,- скажем, по 1 грамму. Получающаяся система трех материальных точек 1А, 1В, 1С имеет однозначно определенный центр масс Z (свойство 1).
В силу свойства 3 положение центра масс не изменится, если массы материальных точек 1В и 1С мы перенесем в их центр масс, т.е. (согласно свойству 2) в точку А1. Но тогда Z окажется центром масс лишь двух материальных точек 2А1 и 1А. Значит, Z є AA1.аналогично убедимся, что Z є ВВ1 и Z є СС1. Таким образом, все три медианы имеют общую точку Z. Кроме того, по правилу рычага (свойство 2) имеем 2ZA1=1ZA или ZA:ZA1=2:1
В силу свойства 3 положение центра масс не изменится, если массы материальных точек 1В и 1С мы перенесем в их центр масс, т.е. (согласно свойству 2) в точку А1. Но тогда Z окажется центром масс лишь двух материальных точек 2А1 и 1А. Значит, Z є AA1.аналогично убедимся, что Z є ВВ1 и Z є СС1. Таким образом, все три медианы имеют общую точку Z. Кроме того, по правилу рычага (свойство 2) имеем 2ZA1=1ZA или ZA:ZA1=2:1
Слайд 9Методы исследования:
Поисковый метод с использованием дополнительной литературы по книге М.В. Балк,
В.Г. Болтянский «Геометрия масс» М «Наука», Библиотечка «Квант», выпуск 61, 1987 год , с. 4 −23.
Метод проб при доказательстве различными способами.
Практический метод обобщения и систематизации, направленный на получении конечного результата.
Умение анализировать , систематизировать и обобщать.
Метод проб при доказательстве различными способами.
Практический метод обобщения и систематизации, направленный на получении конечного результата.
Умение анализировать , систематизировать и обобщать.
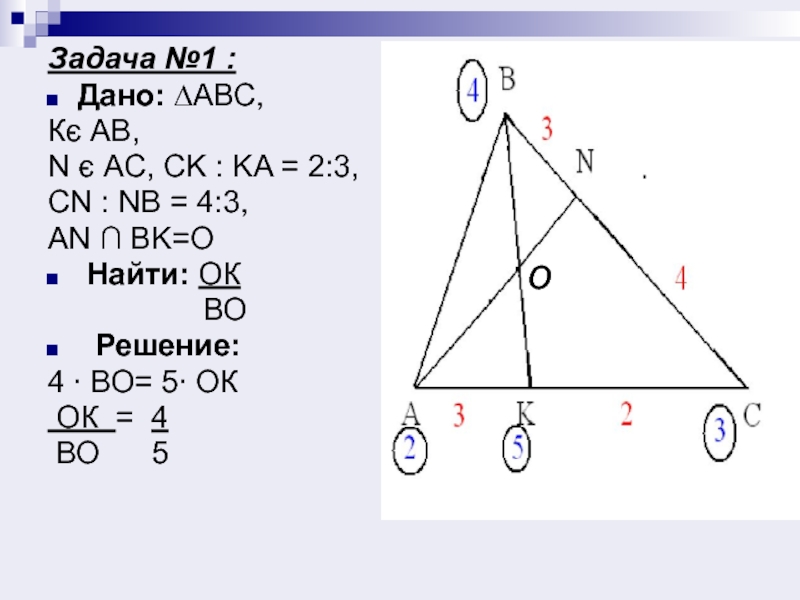
Слайд 10Задача №1 :
Дано: ∆АВС,
Кє АВ,
N є AC, CK :
KA = 2:3,
CN : NB = 4:3,
AN ∩ BK=O
Найти: ОК
ВО
Решение:
4 ∙ ВО= 5∙ ОК
ОК = 4
ВО 5
CN : NB = 4:3,
AN ∩ BK=O
Найти: ОК
ВО
Решение:
4 ∙ ВО= 5∙ ОК
ОК = 4
ВО 5
о
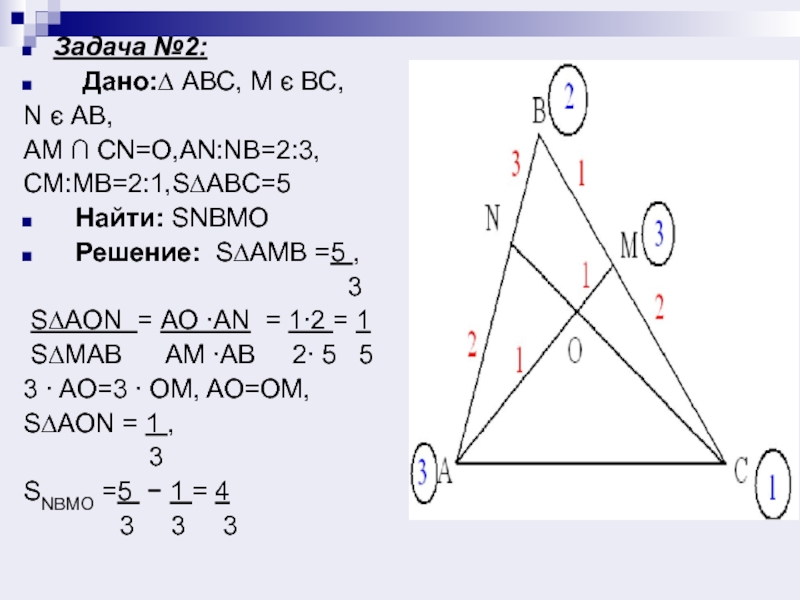
Слайд 11Задача №2:
Дано:∆ АВС, М є ВС,
N є AB,
AM
∩ CN=O,AN:NB=2:3,
CM:MB=2:1,S∆ABC=5
Найти: SNBMO
Решение: S∆АМВ =5 ,
3
S∆AON = AO ∙AN = 1∙2 = 1
S∆MAB AM ∙AB 2∙ 5 5
3 ∙ AO=3 ∙ OM, AO=OM,
S∆AON = 1 ,
3
SNBMO =5 − 1 = 4
3 3 3
CM:MB=2:1,S∆ABC=5
Найти: SNBMO
Решение: S∆АМВ =5 ,
3
S∆AON = AO ∙AN = 1∙2 = 1
S∆MAB AM ∙AB 2∙ 5 5
3 ∙ AO=3 ∙ OM, AO=OM,
S∆AON = 1 ,
3
SNBMO =5 − 1 = 4
3 3 3
Слайд 12 Выводы:
При решении геометрических задач барицентрическим
методом мы загружаем отдельные точки массами с т.е. сопоставляем, приписываем этим точкам определенные положительные числа. Затем привлекаем свойства центров масс всех полученных м.т. или части этих м.т. Искусство применения барицентрического метода состоит в том, чтобы по условию задачи осуществить такой выбор точек и помещаемых в эти точки масс, при котором задача легко и красиво решается. Три основных свойства центров масс особенно важны при решении задач:
Наличие и единственность центра масс у любой системы материальных точек.
Принадлежность центра масс двух материальных точек отрезку, соединяющему эти точки.
Возможность перегруппировки материальных точек системы без изменения положения центра масс всей системы.
Наличие и единственность центра масс у любой системы материальных точек.
Принадлежность центра масс двух материальных точек отрезку, соединяющему эти точки.
Возможность перегруппировки материальных точек системы без изменения положения центра масс всей системы.
Слайд 13 Заключение:
Утверждения и теоремы, доказанные в курсе планиметрии, можно
доказывать используя барицентрический метод.
В работе размещены задачи, которые были предложены при подготовке к Централизованному тестированию и на Централизованном тестировании.
Этот материал может быть изложен на спецкурсе по математике и при подготовке к тестированию.
В работе размещены задачи, которые были предложены при подготовке к Централизованному тестированию и на Централизованном тестировании.
Этот материал может быть изложен на спецкурсе по математике и при подготовке к тестированию.