- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Этот удивительный лист Мёбиуса
Содержание
- 1. Презентация по математике Этот удивительный лист Мёбиуса
- 2. Предисловие Многие знают, что такое лента
- 3. Таинственный и знаменитый лист
- 4. Лист Мёбиуса – один
- 5. Рассказывают, что открыть свой «лист» Мёбиусу помогла служанка, сшившая однажды неправильно концы ленты.Легенда
- 6. Увлекательное исследование Запаситесь несколькими листами обычной белой бумаги, клеем и ножницами. ✂
- 7. Берем бумажную ленту АВСD. Прикладываем
- 8. Получим такое перекрученное кольцо
- 9. ? Зададимся вопросом:
- 10. Красим, не отрываемся, на другую
- 11. Слайд 11
- 12. А вот что получилось у насЛента перекручена два раза
- 13. Теперь сделайте новый лист Мёбиуса
- 14. А вот что получилось у нас
- 15. А если на три части? Три ленты? А ничего подобного! ?
- 16. Получим два сцепленных кольца. Одно
- 17. Человечек - перевертыш.
- 18. Он вернулся к месту старта.
- 19. Исследуйте дальше эту поразительную
- 20. ВыводЛист Мёбиуса – удивительный феномен. Его можно
- 21. Используемая литература: Внеклассная работа по математике В.А.Гусев,
Слайд 2
Предисловие
Многие знают, что такое лента (лист) Мёбиуса.
Слайд 3
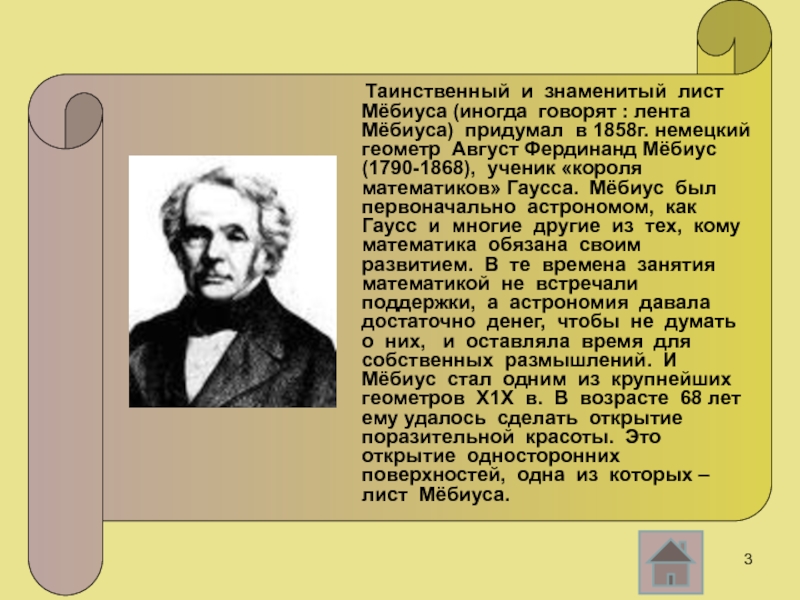
Таинственный и знаменитый лист Мёбиуса (иногда говорят :
Слайд 4
Лист Мёбиуса – один из объектов области математики
Слайд 5
Рассказывают, что открыть свой «лист» Мёбиусу помогла служанка, сшившая однажды
Легенда
Слайд 6 Увлекательное исследование
Запаситесь несколькими листами обычной белой бумаги, клеем
✂
Слайд 7 Берем бумажную ленту АВСD. Прикладываем ее концы АВ и
А
В
С
D
Слайд 9
?
Зададимся вопросом:
сколько сторон у
у любого другого? А ничего подобного. У него ОДНА сторона. Не верите? Хотите – проверьте: попробуйте закрасить это кольцо с одной стороны.
Слайд 10
Красим, не отрываемся, на другую сторону не переходим. Красим...
Слайд 11
Теперь второй вопрос.
Что будет, если разрезать обычный лист бумаги? Конечно же, два обычных листа бумаги. Точнее, две половинки листа.
А что случится, если разрезать вдоль посередине это кольцо (это и есть лист Мёбиуса, или лента Мёбиуса) по всей длине? Два кольца половинной ширины? А ничего подобного. А что? Не скажем. Разрежьте сами.
?
Слайд 13
Теперь сделайте новый лист Мёбиуса и скажите, что будет,
То же самое? А ничего подобного!
?
Слайд 16
Получим два сцепленных кольца. Одно из них вдвое
Слайд 17
Человечек - перевертыш.
Вырежьте бумажного человечка и
Слайд 18
Он вернулся к месту старта. Но в каком виде!
А чтобы он вернулся к старту в нормальном положении, ему нужно совершить ещё одно «круголистное » путешествие.
Проверьте!
Слайд 19
Исследуйте дальше эту поразительную
(и тем не менее
Что может быть полезнее Чистого Знания?
Слайд 20Вывод
Лист Мёбиуса – удивительный феномен. Его можно исследовать до бесконечности, мы
Слайд 21
Используемая литература:
Внеклассная работа по математике В.А.Гусев, А.И.Орлов, А.Л.Розенталь.
Математический цветник
Краткий очерк истории математики. Д. Я. Стройк. Перевод с немецкого и дополнения И.Б.ПОГРЕБЫССКОГО.
Ресурсы:
http://slovari.yandex.ru/dict/bse/article/00046/48100.htm
http://ru.wikipedia.org/wiki/%D0%9B%D0%B8%D1%81%D1%82_%D0%9C%D1%91%D0%B1%D0%B8%D1%83%D1%81%D0%B0
http://www.genon.ru/GetAnswer.aspx?qid=e2ab6eb5-5fb6-4fc6-b1a4-6ee7961a0dc1
www.vokrugsveta.ru
http://shkolazhizni.ru/archive/0/n-13219/
http://www.univer.omsk.su/omsk/Edu/Math/mmebius.htm