- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Элементы комбинаторики
Содержание
- 1. Презентация по математике Элементы комбинаторики
- 2. Что такое комбинаторика?Задачи , решая которые приходится
- 3. Пример 1Из группы теннисистов, в которую входят
- 4. Пример 2Сколько трехзначных чисел можно составить из
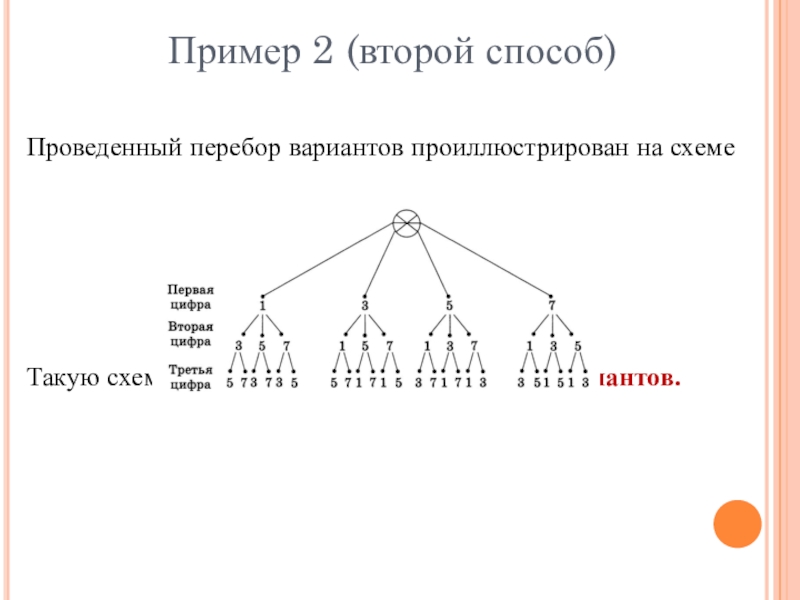
- 5. Проведенный перебор вариантов проиллюстрирован на схемеТакую схему называют деревом возможных вариантов.Пример 2 (второй способ)
- 6. Первую цифру можно выбрать четырьмя способами. Так
- 7. Комбинаторное правило умноженияПусть имеется n элементов и
- 8. ЗадачиПример 1. Из города А в город
- 9. ПерестановкиПерестановкой называется какой-либо способ упорядочения данного множества.
- 10. Первым можно поставить любой из n предметов, вторым –
- 11. ЗадачиПример 1. Сколькими способами могут быть расставлены
- 12. СочетанияСочетанием из n элементов по k называется
- 13. ЗадачиПример 1. Из 15 членов туристической группы
- 14. РазмещенияРазмещением из n элементов по k называется
- 15. Различия между перестановками, размещениями и сочетаниямиВ случае
- 16. ПримерыПример 1. Учащиеся второго класса изучают 8
Что такое комбинаторика?Задачи , решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций , называются комбинаторными.Раздел математики , в котором рассматриваются подобные задачи, называют комбинаторикой.Слово «комбинаторика» от латинского combinare - «соединять
Слайд 2Что такое комбинаторика?
Задачи , решая которые приходится составлять различные комбинации из
конечного числа элементов и подсчитывать число комбинаций , называются комбинаторными.
Раздел математики , в котором рассматриваются подобные задачи, называют комбинаторикой.
Слово «комбинаторика» от латинского combinare - «соединять , сочетать».
Раздел математики , в котором рассматриваются подобные задачи, называют комбинаторикой.
Слово «комбинаторика» от латинского combinare - «соединять , сочетать».
Слайд 3Пример 1
Из группы теннисистов, в которую входят четыре человека - Антонов,
Григорьев , Сергеев и Федоров, тренер выделяет пару для участия в соревнованиях. Сколько существует вариантов выбора такой пары?
АГ, АС, АФ
ГС, ГФ
СФ
Значит, всего существует шесть вариантов выбора.
Способ рассуждений , которым мы воспользовались , называют перебором возможных вариантов.
АГ, АС, АФ
ГС, ГФ
СФ
Значит, всего существует шесть вариантов выбора.
Способ рассуждений , которым мы воспользовались , называют перебором возможных вариантов.
Слайд 4Пример 2
Сколько трехзначных чисел можно составить из цифр 1, 3, 5,
7,используя в записи числа каждую из них не более
одного раза?
Чтобы ответить на вопрос задачи , выпишем все такие числа . Полученные результаты запишем в четыре строки , в каждой из которых шесть чисел:
135 137 153 157 173 175
315 317 351 357 371 375
513 517 531 537 571 573
713 715 731 735 751 753
одного раза?
Чтобы ответить на вопрос задачи , выпишем все такие числа . Полученные результаты запишем в четыре строки , в каждой из которых шесть чисел:
135 137 153 157 173 175
315 317 351 357 371 375
513 517 531 537 571 573
713 715 731 735 751 753
Слайд 5Проведенный перебор вариантов проиллюстрирован на схеме
Такую схему называют деревом возможных вариантов.
Пример
2 (второй способ)
Слайд 6Первую цифру можно выбрать четырьмя способами. Так как после выбора первой
цифры останутся три , то вторую цифру можно выбрать уже тремя способами. Наконец , третью цифру можно выбрать двумя способами. Следовательно , общее число искомых чисел равно произведению 4*3*2,т.е.24.
Использовалось комбинаторное правило умножения.
Использовалось комбинаторное правило умножения.
Пример 2 (третий способ)
Слайд 7Комбинаторное правило умножения
Пусть имеется n элементов и требуется выбрать из них
один за другим k элементов. Если первый элемент можно выбрать n1 способами, после чего второй элемент можно выбрать n2 способами из оставшихся, затем третий элемент можно выбрать n3 способами из оставшихся и т. д., то число способов, которыми могут быть выбраны все k элементов, равно произведению n1 · n2 · n3 · … · nk.
Слайд 8Задачи
Пример 1. Из города А в город В ведут две дороги,
из города В в город С – три дороги , из города С до пристани-две дороги. Туристы хотят проехать из города А через В и С к пристани. Сколькими способами они могут выбрать маршрут?
Пример 2. В кафе предлагают два первых блюда: борщ, рассольник - и четыре вторых блюда: гуляш, котлеты, сосиски, пельмени. Укажите все обеды из двух блюд, которые может заказать посетитель. Построить дерево возможных вариантов.
Пример 2. В кафе предлагают два первых блюда: борщ, рассольник - и четыре вторых блюда: гуляш, котлеты, сосиски, пельмени. Укажите все обеды из двух блюд, которые может заказать посетитель. Построить дерево возможных вариантов.
Слайд 9Перестановки
Перестановкой называется какой-либо способ упорядочения данного множества.
Чтобы найти число всех
перестановок множества из n предметов (это число обозначается Pn, от французского permutation – перестановка) – например, число способов, которыми можно расставить n томов на книжной полке, – обычно рассуждают таким образом.
Слайд 10Первым можно поставить любой из n предметов, вторым – любой из (n – 1) оставшихся
предметов, третьим любой из (n – 2) оставшихся предметов и т. д. В результате число перестановок будет равно произведению n множителей n (n – 1) (n – 2) ... ∙ 3 ∙ 2 ∙ 1.
Для произведения первых n натуральных чисел используют специальное обозначение: n! ( читается n факториал).
Для произведения первых n натуральных чисел используют специальное обозначение: n! ( читается n факториал).
Перестановки
Слайд 11Задачи
Пример 1. Сколькими способами могут быть расставлены 8 участниц финального забега
на восьми беговых дорожках?
Пример 2. Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0, 2, 4, 6?
Пример 2. Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0, 2, 4, 6?
Слайд 12Сочетания
Сочетанием из n элементов по k называется комбинация, в которой из
этих n элементов выбраны любые k без учета их порядка в комбинации.
Таким образом, для сочетания имеет значение только состав выбранных элементов, а не их порядок.
Таким образом, для сочетания имеет значение только состав выбранных элементов, а не их порядок.
Слайд 13Задачи
Пример 1. Из 15 членов туристической группы надо выбрать трех дежурных.
Сколькими способами можно сделать этот выбор?
Пример 2. Из вазы с фруктами, в которой лежит 9 яблок и 6 груш, надо выбрать 3 яблока и 2 груши. Сколькими способами можно сделать такой выбор?
Пример 2. Из вазы с фруктами, в которой лежит 9 яблок и 6 груш, надо выбрать 3 яблока и 2 груши. Сколькими способами можно сделать такой выбор?
Слайд 14Размещения
Размещением из n элементов по k называется комбинация, в которой какие-то
k из этих n элементов расположены в определенном порядке.
Размещения отличаются друг от друга не только порядком расположения элементов, но и тем, какие именно k элементов выбраны в комбинацию.
Размещения отличаются друг от друга не только порядком расположения элементов, но и тем, какие именно k элементов выбраны в комбинацию.
Слайд 15Различия между перестановками, размещениями и сочетаниями
В случае перестановок берутся все элементы
и изменяется только их местоположение.
В случае размещений берётся только часть элементов и важно расположение элементов друг относительно друга.
В случае сочетаний берётся только часть элементов и не имеет значения расположение элементов друг относительно друга.
В случае размещений берётся только часть элементов и важно расположение элементов друг относительно друга.
В случае сочетаний берётся только часть элементов и не имеет значения расположение элементов друг относительно друга.
Слайд 16Примеры
Пример 1. Учащиеся второго класса изучают 8 предметов. Сколькими способами можно
составить расписание на один день, чтобы в нем было 4 различных предмета?
Пример 2. Сколько трехзначных чисел ( без повторения цифр в записи числа) можно составить из цифр 0,1,2,3,4,5,6?
Пример 2. Сколько трехзначных чисел ( без повторения цифр в записи числа) можно составить из цифр 0,1,2,3,4,5,6?