Галина Васильевна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Его Величество граф (5-6 класс)
Содержание
- 1. Презентация по математике Его Величество граф (5-6 класс)
- 2. Человек, желающий стать математиком,с первых шагов должен
- 3. Впервые с задачами, для решения которых используются
- 4. математиков и по сей день. Она была
- 5. Это были первые успехи наших познаний. В
- 6. ВведениеС дворянским титулом «граф» тему моей работы
- 7. ЦЕЛЬРазвивать интерес к предмету математика.Сформировать представление о
- 8. ЗАДАЧИПровести опрос среди учащихся по данной
- 9. ЭТАПЫ ПРОЕКТАИзучение специальной научной литературыПрименение методов решения
- 10. АКТУАЛЬНОСТЬнеобходимость решать алгебраические и математические задачи различными
- 11. Гипотеза исследования. Чем отличаются решение задач с
- 12. Ожидаемые результатыФормирование логико-алгоритмического и системно-комбинаторного мышления;Формирование опыта исследовательской работы
- 13. Зачем изучать теорию графовВ последние десятилетия происходит
- 14. СодержаниеИстория возникновения графовИзбранные задачи теории графовОдним росчерком
- 15. Описание полученных результатовСформированы логико-алгоритмическое и системно-комбинированное мышленияПриобретен опыт исследовательской деятельности
- 16. Результаты опроса
- 17. 1. Основные понятия теории графовГраф – система,
- 18. Что такое графСлово «граф» в математике означает
- 19. ..В математике определение графа дается так:Графом называется
- 20. .Количество рёбер, выходящих из вершины графа, называется
- 21. ГРАФ НАЗЫВАЕТСЯ ПОЛНЫМ, ЕСЛИ ЛЮБЫЕ ДВЕ ЕГО
- 22. История возникновения графовОсновы теории графов как математической
- 23. Задача о Кенигсбергских мостахБывший Кенигсберг (ныне Калининград)
- 24. Задача о Кенигсбергских мостахКенигсбергцы предлагали приезжим следующую
- 25. Задача о Кенигсбергских мостахПройти по Кенигсбергским мостам,
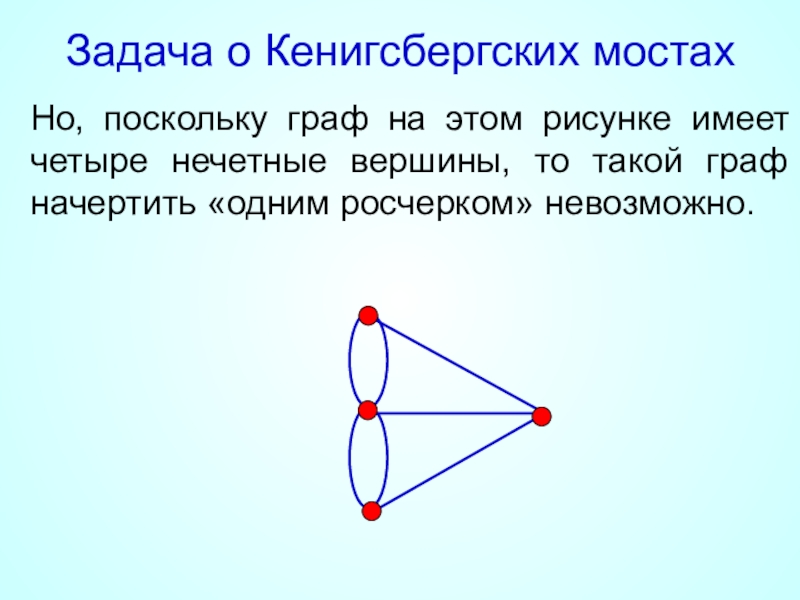
- 26. Задача о Кенигсбергских мостахНо, поскольку граф на
- 27. Избранные задачи1. В 10-значном числе каждые две подряд
- 28. .2. В деревне 10 домов, и из каждого
- 29. .. Сколько диагоналей в 17-угольнике?Решение. Вершины 17-угольника – вершины
- 30. .В офисе компании «Суперботан» 129 телефонов. Можно
- 31. Одним росчеркомГраф, который можно нарисовать, не отрывая
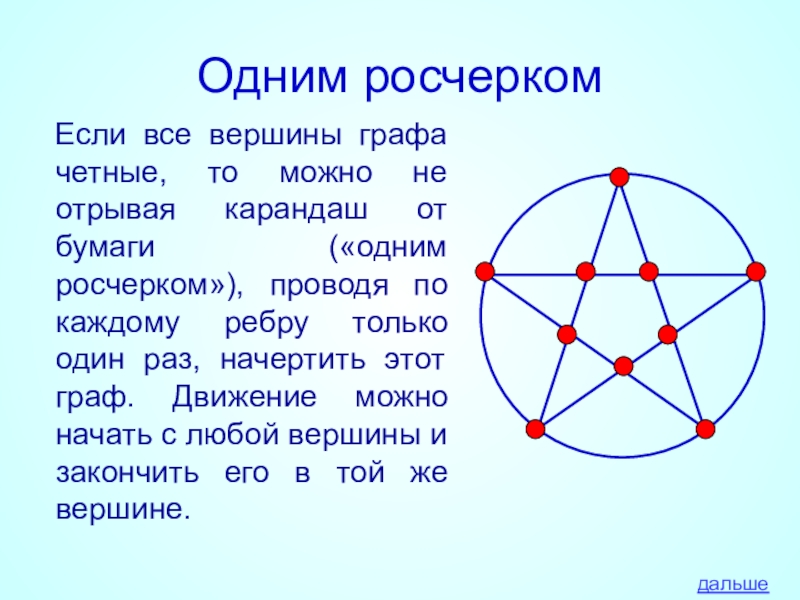
- 32. Одним росчеркомЕсли все вершины графа четные, то
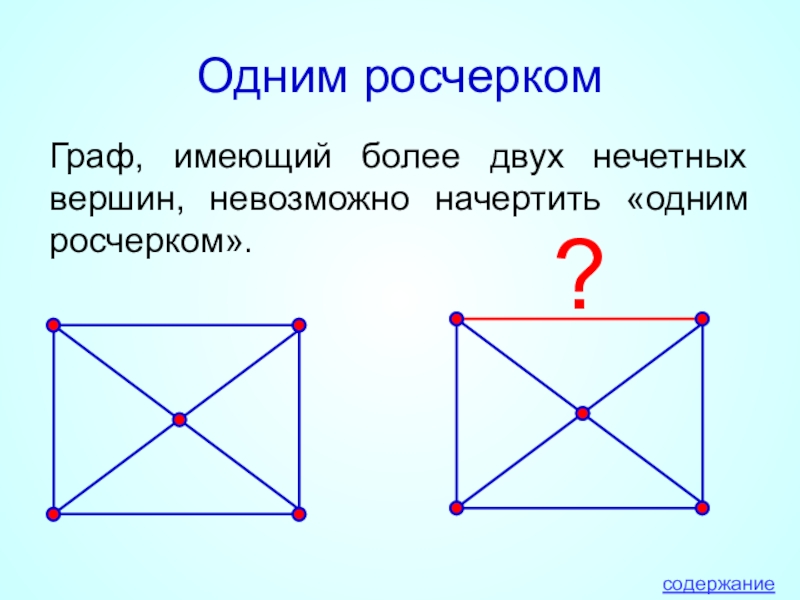
- 33. Одним росчеркомГраф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком». ?содержание
- 34. Слайд 34
- 35. Применение графовПроисхождение задач о лабиринтах относится к
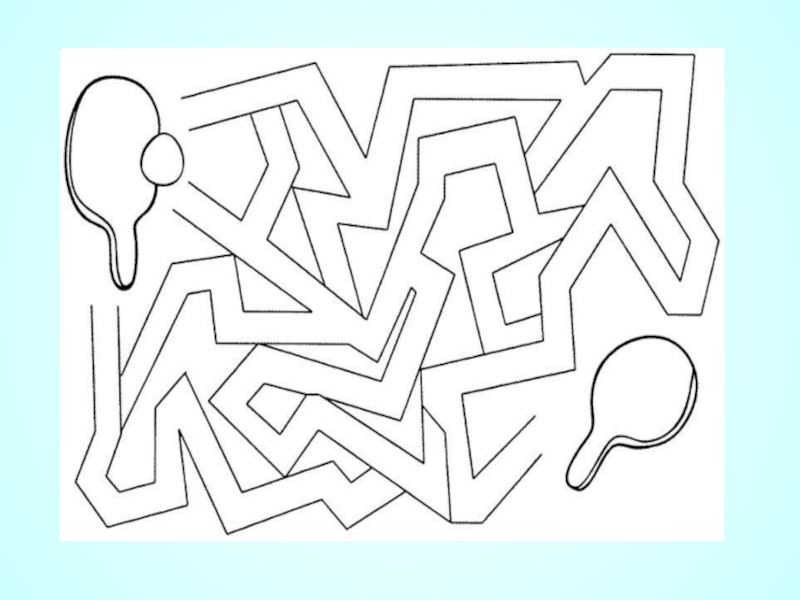
- 36. .Лабиринт - это граф. А исследовать его - это найти путь в этом графе. дальше
- 37. Слайд 37
- 38. Первый многосвязный садовый лабиринт был сооружён в 1820-е годы в Чевнинге в Великобритании.
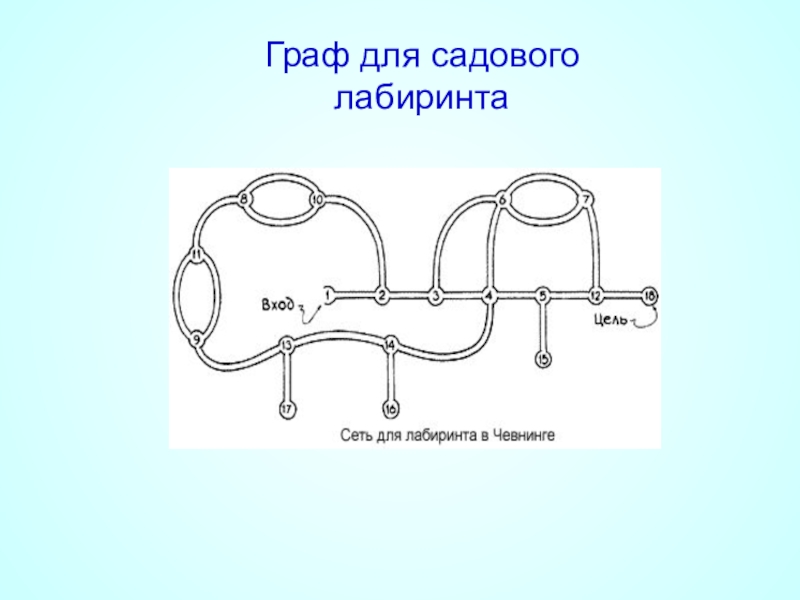
- 39. Граф для садового лабиринта
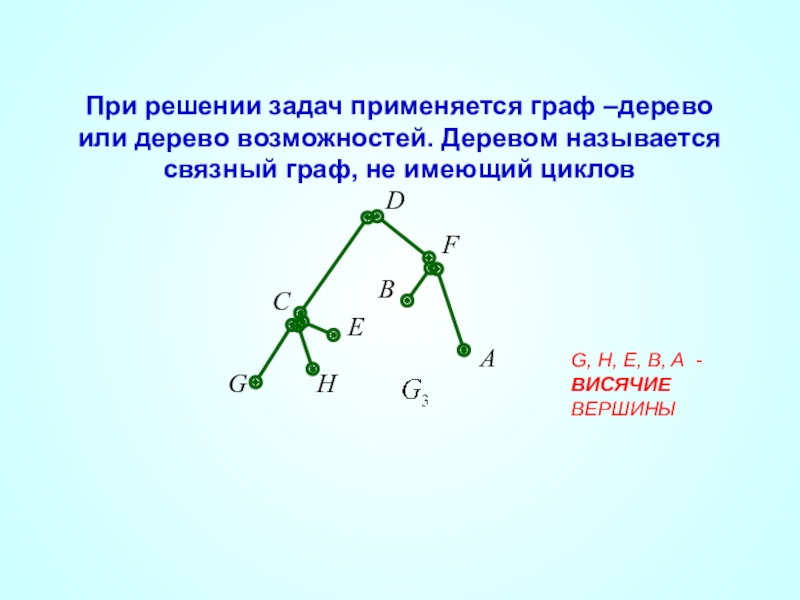
- 40. G, H, E, B, A - ВИСЯЧИЕ
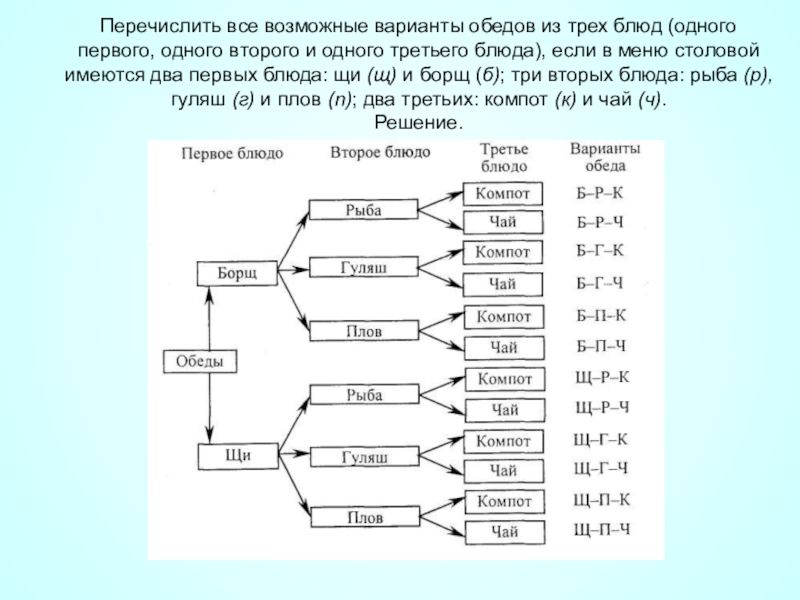
- 41. Перечислить все возможные варианты обедов из трех
- 42. Применение графовЗадача:Аркадий, Борис. Владимир, Григорий и Дмитрий
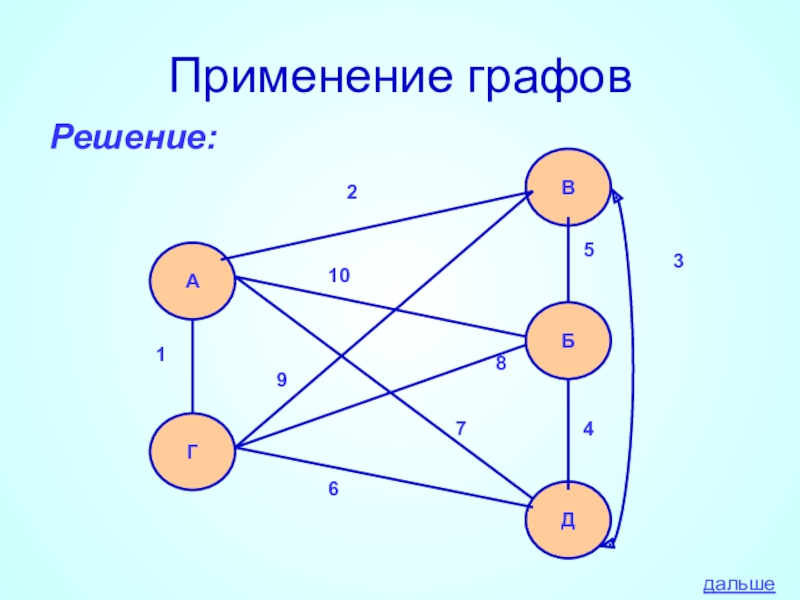
- 43. Применение графовРешение:АГВБД12345678910дальше
- 44. Задача 2. По окончании деловой встречи специалисты
- 45. Логические задачи
- 46. Число в скобках называют степенью вершины, оно
- 47. Начать построение ребер следует с вершины В,
- 48. Для вершин В и Ж построены все
- 49. Теперь однозначно определяются ребра вершины Т.С
- 50. Все возможные ребра теперь построены для вершин
- 51. ОТВЕТ: Леша играл с Толей, Ваней
- 52. В одном дворе живут четыре друга. Вадим
- 53. ВадимКоляСергейАндрейслесарьтокарьэлектрикшоферНачинаем анализировать полученную схему.От каждого верхнего кружка
- 54. Андрей, Борис, Володя, Даша, Галя договорились созвониться
- 55. Применение графовИспользует графы и дворянство.На рисунке приведена
- 56. Мое генеалогическое дерево
- 57. Эссе.Моё исследование ещё раз доказало, что всё
- 58. ВЫВОДЫТеория графов является фундаментальной и имеет широкую
- 59. Выводы.. В математике существует специальный раздел, который
- 60. Графы нашли применение во всех отраслях научных
- 61. СПИСОК ЛИТЕРАТУРЫ:1. М. В. Ткачева, Домашняя математика:
- 62. Список литературы 7.Виленкин Н.Я КомбинаторикаЖ:Наука 1969 год8.
- 63. Спасибо за внимание
Человек, желающий стать математиком,с первых шагов должен любить и ценить эту красоту мысли, стройность выводов и построений, часто неожиданных и сильных!
Слайд 1ЕГО ВЕЛИЧЕСТВО ГРАФ
.
Работу выполнила
Ученица 5 класса А
Университетского лицея
Города Димитровграда
Климчук Яна
Учитель: Давыдова
Слайд 2Человек, желающий стать математиком,
с первых шагов должен любить и ценить эту
красоту мысли, стройность выводов и построений, часто неожиданных и сильных!
С.Л.Соболев
С.Л.Соболев
Слайд 3Впервые с задачами, для решения которых используются графы, мы встретились на
уроках математики. Трудности в решении этих задач объяснялись отсутствием этой темы в обязательном курсе школьной математики. Возникшая проблема стала главной причиной выбора данной исследовательской работы. Математические развлечения, головоломки тоже являются частью теории графов, например, знаменитая задача четырех красок, интригующая
Слайд 4математиков и по сей день. Она была выдвинута Мебиусом в 1840году.
«Для всякой карты достаточно 4различных красок, чтобы любые две области, имеющие общую границу, не были окрашены одним цветом: причем все равно, сколько областей, как причудливы их очертания и как сложно их взаимное расположение. Тема актуальна тем, что предположение о 4 красках никто не доказал, но и никто и не опроверг.
Слайд 5Это были первые успехи наших познаний. В процессе работы я обращалась
к дополнительным источникам информации, что способствовало развитию самообразовательных навыков. Кроме того, расширились знания по другим предметам: истории, географии, информатике.
Слайд 6Введение
С дворянским титулом «граф» тему моей работы связывает только общее происхождение
от латинского слова «графио» - пишу.
Г
Р
А
Ф
И
О
дальше
Слайд 7ЦЕЛЬ
Развивать интерес к предмету математика.
Сформировать представление о значении теории графов как
средства описания действительности
Развивать логическое мышление, умение анализировать при решении задач.
Выяснить, где применяется теория графов.
Развивать логическое мышление, умение анализировать при решении задач.
Выяснить, где применяется теория графов.
Слайд 8 ЗАДАЧИ
Провести опрос среди учащихся по данной теме, составить генеалогическое дерево
Проанализировать
полученные результаты и изучить литературу
Экспериментально проверить, как можно применять изученные методы при решении нетипичных задач
Сформулировать выводы
Выступить с презентацией
Экспериментально проверить, как можно применять изученные методы при решении нетипичных задач
Сформулировать выводы
Выступить с презентацией
Слайд 9ЭТАПЫ ПРОЕКТА
Изучение специальной научной литературы
Применение методов решения задач при помощи теории
графов на практике
Составление текста выступления перед одноклассниками
Создание мультимедийной презентации
Защита проекта
Составление текста выступления перед одноклассниками
Создание мультимедийной презентации
Защита проекта
Слайд 10АКТУАЛЬНОСТЬ
необходимость решать алгебраические и математические задачи различными способами
объект исследования: процесс
решения нестандартных задач
предмет исследования: развитие навыка построения графических схем, развитие умения решать нетипичные задачи курса математики.
предмет исследования: развитие навыка построения графических схем, развитие умения решать нетипичные задачи курса математики.
Слайд 11Гипотеза исследования.
Чем отличаются решение задач с графами друг от друга?
Графы помогают
легко находить вероятность в задачах различного уровня сложности.
Слайд 12Ожидаемые результаты
Формирование логико-алгоритмического и системно-комбинаторного мышления;
Формирование опыта исследовательской работы
Слайд 13Зачем изучать теорию графов
В последние десятилетия происходит значительное увеличение интереса к
теории графов. Зародившись более 200 лет назад при решении головоломок и занимательных задач, она стала в настоящее время простым, доступным и мощным средством решения широкого круга важных практических задач. Особенно велико значение графов как универсального языка при создании математических моделей. Построенные модели можно эффективно исследовать с помощью компьютера. Возникает вопрос: нужен ли граф? Попробуйте решить задачи без использования графов.
Слайд 14Содержание
История возникновения графов
Избранные задачи теории графов
Одним росчерком
Применение теории графов
Гамильтоновый путь
графа
Как решить логическую задачу с помощью графов
Как решить логическую задачу с помощью графов
Литература
Слайд 15Описание полученных результатов
Сформированы логико-алгоритмическое и системно-комбинированное мышления
Приобретен опыт исследовательской деятельности
Слайд 16 Результаты опроса Знания теории графов у учащихся 5-6классов. - знают определение графов, но
не решали задачи-10
-не знают определение графов, но решали задачи-18
-знают определение графов и решали задачи-8
-не знают определения-86
Слайд 171. Основные понятия теории графов
Граф – система, которая интуитивно может быть
рассмотрена как множество кружков и множество соединяющих их линий (геометрический способ задания графа). Кружки называются вершинами графа, линии со стрелками – дугами, без стрелок – ребрами. Граф, в котором направление линий не выделяется (все линии являются ребрами), называется неориентированным; граф, в котором направление линий принципиально (линии являются дугами) называется ориентированным.
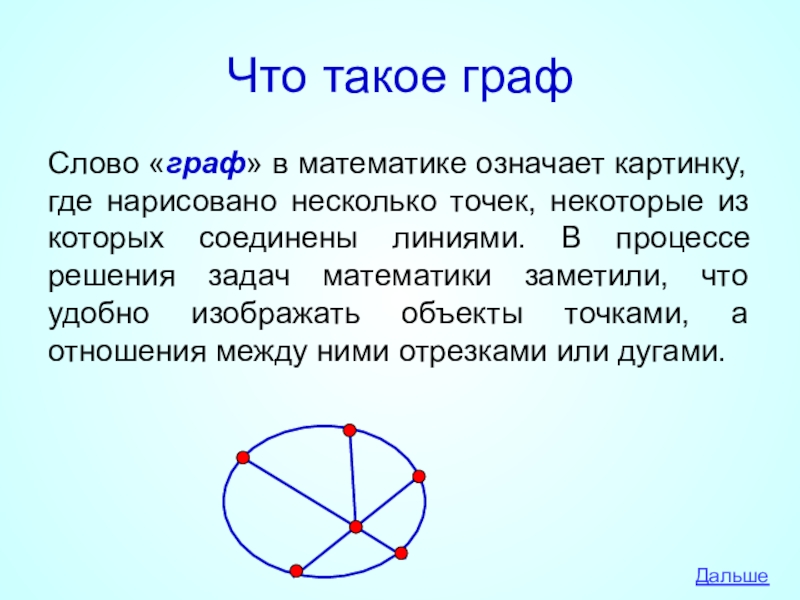
Слайд 18Что такое граф
Слово «граф» в математике означает картинку, где нарисовано несколько
точек, некоторые из которых соединены линиями. В процессе решения задач математики заметили, что удобно изображать объекты точками, а отношения между ними отрезками или дугами.
Дальше
Слайд 19..
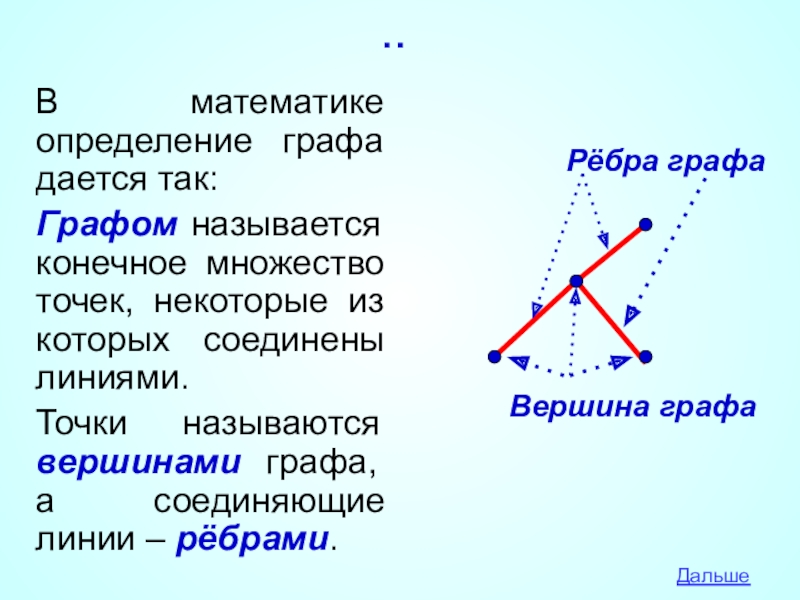
В математике определение графа дается так:
Графом называется конечное множество точек, некоторые
из которых соединены линиями.
Точки называются вершинами графа, а соединяющие линии – рёбрами.
Точки называются вершинами графа, а соединяющие линии – рёбрами.
Рёбра графа
Вершина графа
Дальше
Слайд 20.
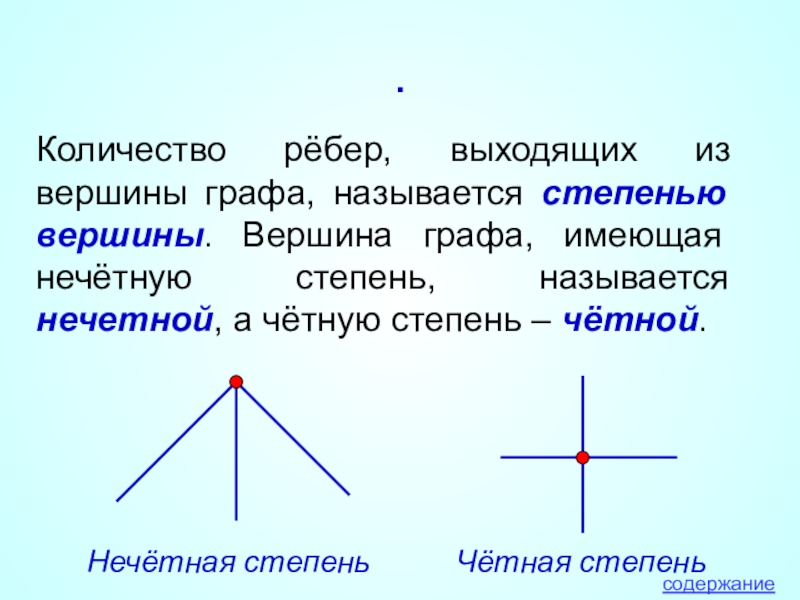
Количество рёбер, выходящих из вершины графа, называется степенью вершины. Вершина графа,
имеющая нечётную степень, называется нечетной, а чётную степень – чётной.
Нечётная степень
Чётная степень
содержание
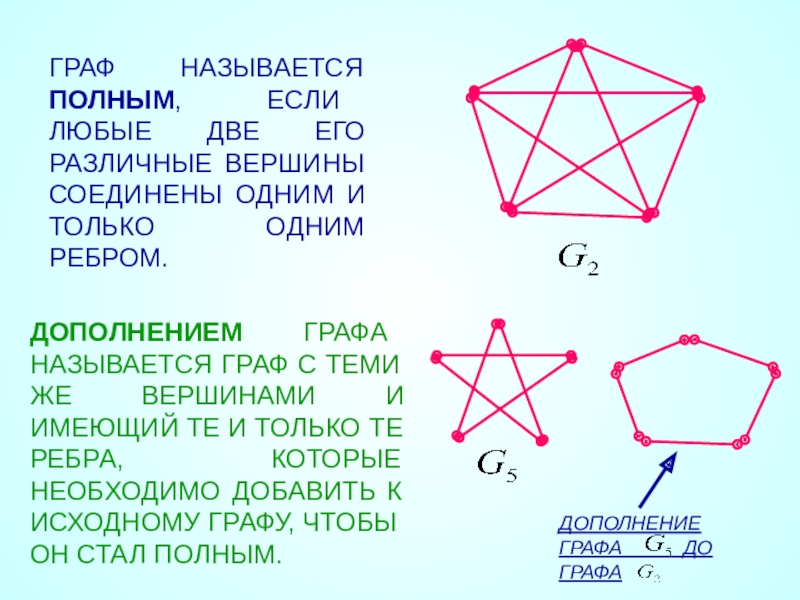
Слайд 21ГРАФ НАЗЫВАЕТСЯ ПОЛНЫМ, ЕСЛИ ЛЮБЫЕ ДВЕ ЕГО РАЗЛИЧНЫЕ ВЕРШИНЫ СОЕДИНЕНЫ ОДНИМ
И ТОЛЬКО ОДНИМ РЕБРОМ.
ДОПОЛНЕНИЕМ ГРАФА НАЗЫВАЕТСЯ ГРАФ С ТЕМИ ЖЕ ВЕРШИНАМИ И ИМЕЮЩИЙ ТЕ И ТОЛЬКО ТЕ РЕБРА, КОТОРЫЕ НЕОБХОДИМО ДОБАВИТЬ К ИСХОДНОМУ ГРАФУ, ЧТОБЫ ОН СТАЛ ПОЛНЫМ.
ДОПОЛНЕНИЕ ГРАФА ДО ГРАФА
Слайд 22История возникновения графов
Основы теории графов как математической науки заложил в 1736
г. Леонард Эйлер, рассматривая задачу о Кенигсбергских мостах. Сегодня эта задача стала классической.
содержание
Слайд 23Задача о Кенигсбергских мостах
Бывший Кенигсберг (ныне Калининград) расположен на реке Прегель.
В пределах города река омывает два острова. С берегов на острова были перекинуты мосты. Старые мосты не сохранились, но осталась карта города, где они изображены.
Дальше
Слайд 24Задача о Кенигсбергских мостах
Кенигсбергцы предлагали приезжим следующую задачу: пройти по всем
мостам и вернуться в начальный пункт, причём на каждом мосту следовало побывать только один раз.
Дальше
Слайд 25Задача о Кенигсбергских мостах
Пройти по Кенигсбергским мостам, соблюдая заданные условия, нельзя.
Прохождение по всем мостам при условии, что нужно на каждом побывать один раз и вернуться в точку начала путешествия, на языке теории графов выглядит как задача изображения «одним росчерком» графа.
Слайд 26Задача о Кенигсбергских мостах
Но, поскольку граф на этом рисунке имеет четыре
нечетные вершины, то такой граф начертить «одним росчерком» невозможно.
Слайд 27Избранные задачи
1. В 10-значном числе каждые две подряд идущие цифры образуют двузначное
число, которое делится на 13. Докажите, что среди этих цифр нет цифры 8.
Решение. Существует 7 двузначных чисел, которые делятся на 13. Обозначим эти числа точками и применим определение графа. По условию каждые 2 подряд идущие цифры образуют двузначное число, которые делятся на 13, значит цифры, из которых состоит 10-значное число, повторяются. Соединим вершины графа рёбрами так , чтобы цифры, входящие в этот граф повторялись.
13 65
78
91 39 52
26
Из построенных графов видно, что среди цифр 10-значного числа цифры 8 быть не может.
Решение. Существует 7 двузначных чисел, которые делятся на 13. Обозначим эти числа точками и применим определение графа. По условию каждые 2 подряд идущие цифры образуют двузначное число, которые делятся на 13, значит цифры, из которых состоит 10-значное число, повторяются. Соединим вершины графа рёбрами так , чтобы цифры, входящие в этот граф повторялись.
13 65
78
91 39 52
26
Из построенных графов видно, что среди цифр 10-значного числа цифры 8 быть не может.
Слайд 28.
2. В деревне 10 домов, и из каждого выходит по 7 тропинок,
идущих к другим домам. Сколько всего тропинок проходит между домами?
Решение. Пусть дома- вершины графа, тропинки- рёбра. По условию из каждого дома (вершины) выходит 7 тропинок (рёбер), тогда степень каждой вершины 7, сумма степеней вершин 7×10=70, а число рёбер 70 : 2= 35. Таким образом между домами проходит 35 тропинок.
Решение. Пусть дома- вершины графа, тропинки- рёбра. По условию из каждого дома (вершины) выходит 7 тропинок (рёбер), тогда степень каждой вершины 7, сумма степеней вершин 7×10=70, а число рёбер 70 : 2= 35. Таким образом между домами проходит 35 тропинок.
Можно ли найти 5 натуральных чисел, таких, что для каждого из них среди оставшихся чисел найдётся ровно три числа с одинаковым простым делителем?
Решение. Представим себе, что мы нашли таких 5 чисел. Пусть эти числа будут вершинами графа. Если два числа имеют одинаковый простой делитель, соединим их ребром. Степень каждой вершины такого графа равна 3, а вершин 5 получим, что сумма степеней вершин графа 3×5=15 – нечётное число. По лемме 2 сумма степеней вершин графа чётна, значит таких 5 чисел найти нельзя.
Слайд 29.
. Сколько диагоналей в 17-угольнике?
Решение. Вершины 17-угольника – вершины графа, а диагонали и
стороны – ребра графа. Всего 17×(17-1) : 2 = 136 ребер. Из них 17 сторон, остальные диагонали. Значит, диагоналей 136 – 17 = 119.
.На рисунке изображены расстояния между пунктами A, B, C, D, E и F. Двигаться по дорогам можно только в направлениях, указанных стрелочками. Водитель едет из пункта А в пункт Е. Как он должен ехать, чтобы добраться по самому короткому пути?
C D
A E
B F
Решение. Рассмотрим последовательно возможные пути поездки и сравним их длину. ABFE = 14, ABFCDE = 15, ABFDE = 13, ACDE = 16.Выберем наименьшее расстояние. Оно равно 13, значит нужно ехать по маршруту ABFDE.
Слайд 30.
В офисе компании «Суперботан» 129 телефонов. Можно ли их соединить проводами
так, чтобы каждый телефон был соединен, ровно с семью другими?
Решение. Пусть каждый телефон является вершиной графа, тогда степень каждой вершины равна 7, а сумма степеней всех вершин равна 129×7 = 903-число нечетное. По лемме 2 сумма степеней вершин графа четна, значит соединить телефоны указанным образом нельзя.
Решение. Пусть каждый телефон является вершиной графа, тогда степень каждой вершины равна 7, а сумма степеней всех вершин равна 129×7 = 903-число нечетное. По лемме 2 сумма степеней вершин графа четна, значит соединить телефоны указанным образом нельзя.
Слайд 31Одним росчерком
Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется
эйлеровым.
Решая задачу О кенигсбергских мостах, Эйлер сформулировал свойства графа:
Невозможно начертить граф с нечетным числом нечетных вершин.
Решая задачу О кенигсбергских мостах, Эйлер сформулировал свойства графа:
Невозможно начертить граф с нечетным числом нечетных вершин.
дальше
Слайд 32Одним росчерком
Если все вершины графа четные, то можно не отрывая карандаш
от бумаги («одним росчерком»), проводя по каждому ребру только один раз, начертить этот граф. Движение можно начать с любой вершины и закончить его в той же вершине.
дальше
Слайд 33Одним росчерком
Граф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком».
?
содержание
Слайд 35Применение графов
Происхождение задач о лабиринтах относится к глубокой древности. Слово «лабиринт»
(греческое) означает «ходы в подземельях» (например, линии электропередач, канализации. сетей дорог, каналов и др.)
Слайд 38Первый многосвязный садовый лабиринт был сооружён в 1820-е годы в Чевнинге
в Великобритании.
Слайд 40G, H, E, B, A - ВИСЯЧИЕ ВЕРШИНЫ
При решении задач применяется
граф –дерево или дерево возможностей. Деревом называется связный граф, не имеющий циклов
Слайд 41Перечислить все возможные варианты обедов из трех блюд (одного первого, одного
второго и одного третьего блюда), если в меню столовой имеются два первых блюда: щи (щ) и борщ (б); три вторых блюда: рыба (р), гуляш (г) и плов (n); два третьих: компот (к) и чай (ч).
Решение.
Решение.
Слайд 42Применение графов
Задача:
Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями
(каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано?
дальше
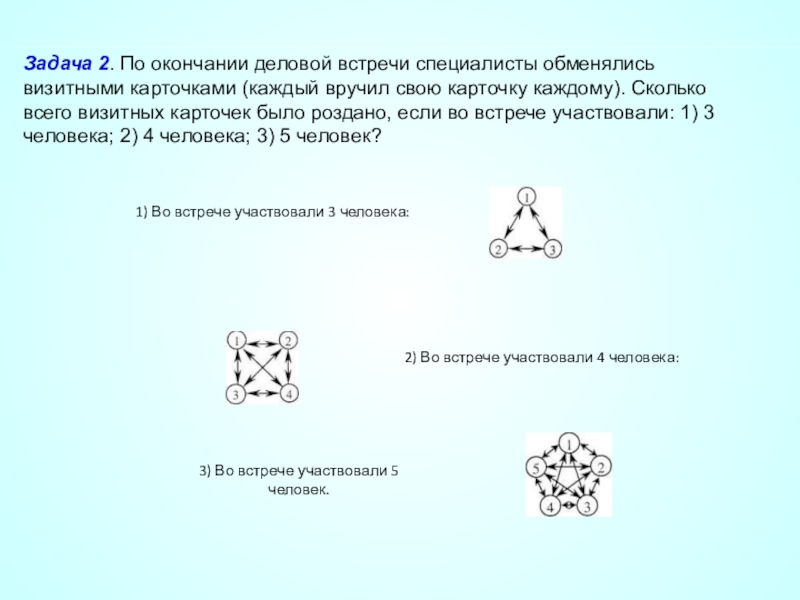
Слайд 44Задача 2. По окончании деловой встречи специалисты обменялись визитными карточками (каждый
вручил свою карточку каждому). Сколько всего визитных карточек было роздано, если во встрече участвовали: 1) 3 человека; 2) 4 человека; 3) 5 человек?
1) Во встрече участвовали 3 человека:
2) Во встрече участвовали 4 человека:
3) Во встрече участвовали 5 человек.
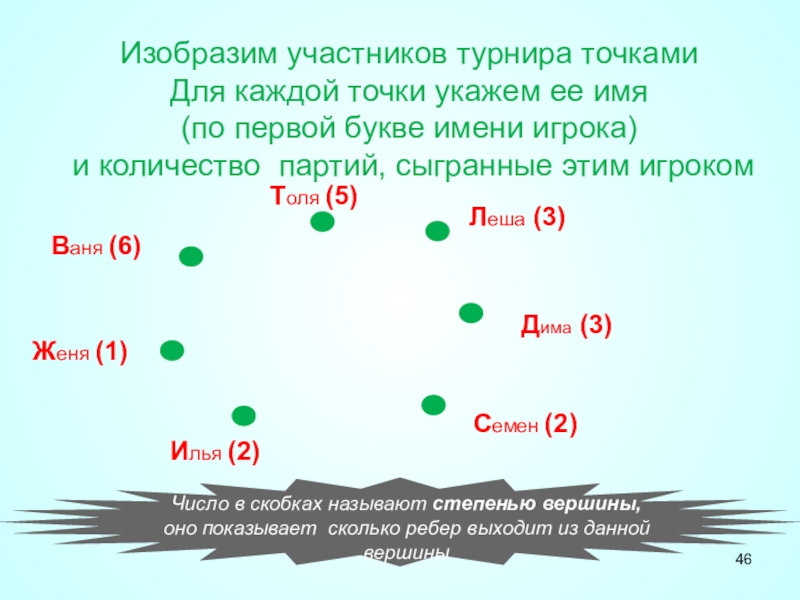
Слайд 46Число в скобках называют степенью вершины, оно показывает сколько ребер выходит
из данной вершины
Ваня (6)
Толя (5)
Леша (3)
Дима (3)
Семен (2)
Илья (2)
Женя (1)
Изобразим участников турнира точками
Для каждой точки укажем ее имя
(по первой букве имени игрока)
и количество партий, сыгранные этим игроком
Слайд 47Начать построение ребер следует с вершины В, так как это единственная
вершина,
которая соединяется со всеми другими вершинами графа
которая соединяется со всеми другими вершинами графа
Ваня (6)
Толя (5)
Леша (3)
Дима (3)
Семен (2)
Илья (2)
Женя (1)
Будем строить ребра графа с учетом степеней вершин
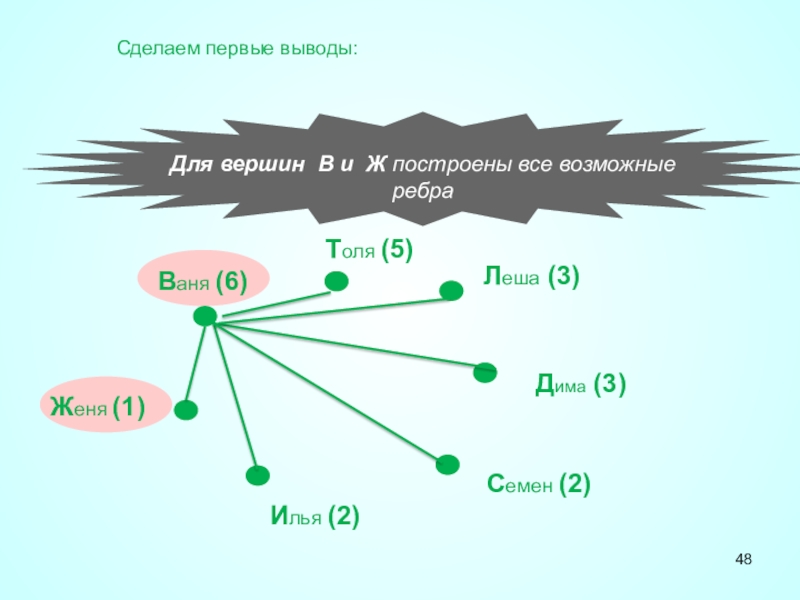
Слайд 48Для вершин В и Ж построены все возможные ребра
Ваня (6)
Толя (5)
Леша
(3)
Дима (3)
Семен (2)
Илья (2)
Женя (1)
Сделаем первые выводы:
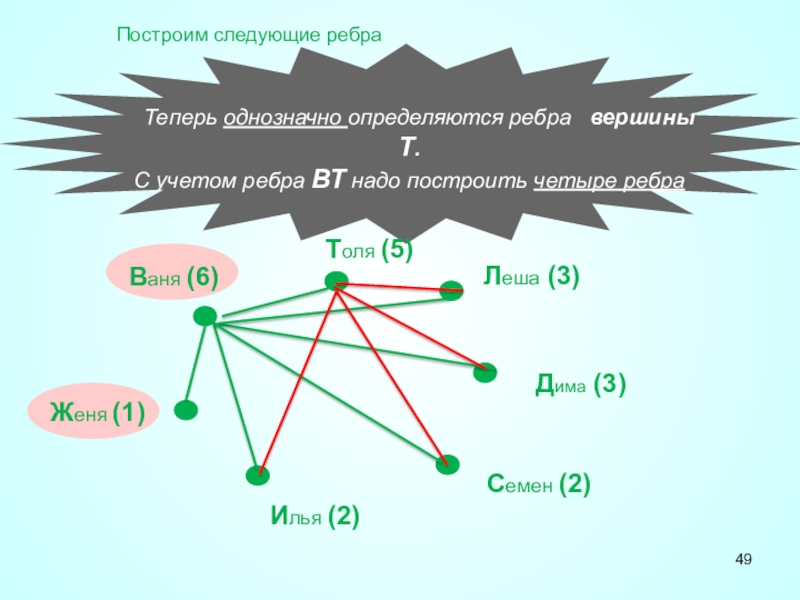
Слайд 49Теперь однозначно определяются ребра вершины Т.
С учетом ребра ВТ надо
построить четыре ребра
Ваня (6)
Толя (5)
Леша (3)
Дима (3)
Семен (2)
Илья (2)
Женя (1)
Построим следующие ребра
Слайд 50Все возможные ребра теперь построены для вершин Ж, В,
Т, а также для вершин С и И
Ваня (6)
Толя (5)
Леша (3)
Дима (3)
Семен (2)
Илья (2)
Женя (1)
Пора делать новые выводы
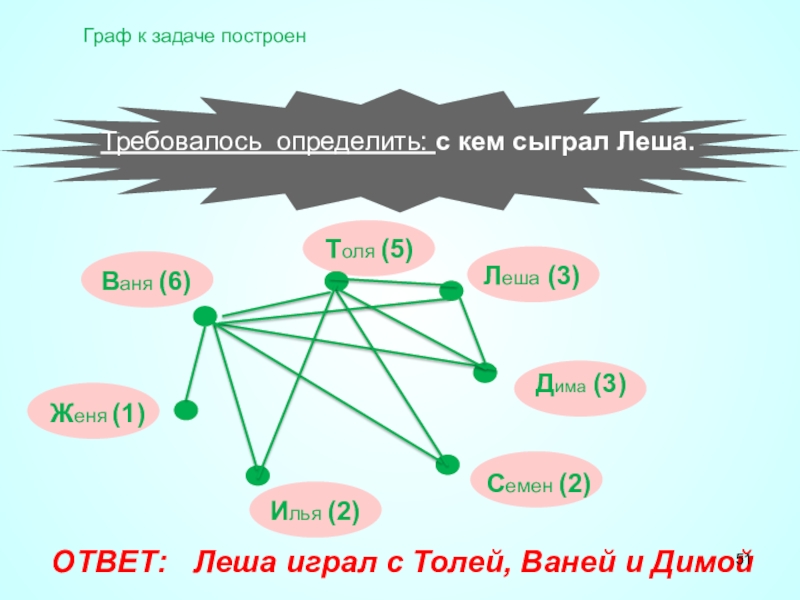
Слайд 51ОТВЕТ: Леша играл с Толей, Ваней и Димой
Ваня (6)
Толя (5)
Леша
(3)
Дима (3)
Семен (2)
Илья (2)
Женя (1)
Требовалось определить: с кем сыграл Леша.
Граф к задаче построен
Слайд 52В одном дворе живут четыре друга.
Вадим и шофер старше Сергея,
Николай
и слесарь занимаются боксом,
Электрик-младший из друзей.
По вечерам Андрей и токарь играют в домино против Сергея и электрика.
Определите профессию каждого из друзей.
Электрик-младший из друзей.
По вечерам Андрей и токарь играют в домино против Сергея и электрика.
Определите профессию каждого из друзей.
Задача, решаемая с помощью графов.
Слайд 53Вадим
Коля
Сергей
Андрей
слесарь
токарь
электрик
шофер
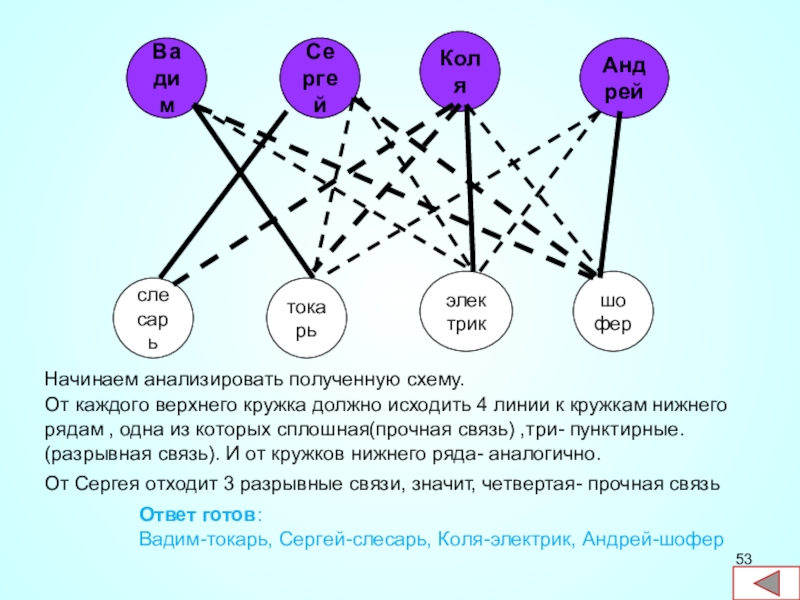
Начинаем анализировать полученную схему.
От каждого верхнего кружка должно исходить 4 линии
к кружкам нижнего рядам , одна из которых сплошная(прочная связь) ,три- пунктирные. (разрывная связь). И от кружков нижнего ряда- аналогично.
От Сергея отходит 3 разрывные связи, значит, четвертая- прочная связь
Ответ готов:
Вадим-токарь, Сергей-слесарь, Коля-электрик, Андрей-шофер
Слайд 54Андрей, Борис, Володя, Даша, Галя договорились созвониться по телефону о посещении
кино. Вечером у кинотеатра собрались не все. На следующий день стали выяснять, кто кому звонил. Оказалось, что Андрей звонил Борису и Володе, Володя звонил Борису и Даше, Борис звонил Андрею и Даше, Даша – Андрею и Володе, а Галя – Андрею, Володе и Борису. Кто не пришёл в кино, если все они условились, что поход в кино состоится только в том случае, если созвонятся все?
Задача.
Слайд 55Применение графов
Использует графы и дворянство.
На рисунке приведена часть генеалогического дерева знаменитого
дворянского рода Л. Н. Толстого. Здесь его вершины – члены этого рода, а связывающие их отрезки – отношения родственности, ведущие от родителей к детям.
дальше
Слайд 57Эссе.
Моё исследование ещё раз доказало, что всё в нашей жизни, а
значит и в изучении математики происходит «не просто так». Всё закономерно и логично. Если ты изучаешь что-то новое, то обязательно будет результат!
Слайд 58ВЫВОДЫ
Теория графов является фундаментальной и имеет широкую область применения
«Графы- это замечательные
математические объекты, с помощью которых решаются различные задачи.
Теория графов- одна из самых красивых и наглядных математических теорий
Теория графов- одна из самых красивых и наглядных математических теорий
Слайд 59Выводы.
. В математике существует специальный раздел, который называется «Теория графов» В
своей работе я исследовала самые основные понятия и свойства графов. Данные наработки мы используем при решении задач на уроках математики , на занятиях математического и психологического кружков. Язык графов прост, доступен и понятен. С использованием теории графов мы решали гораздо больше задач. Изучая это тему, я узнала, что теорию графов мы будем применять и на уроках литературы, биологии, физики, химии. В дальнейшем я хочу продолжить работу по изучению теории графов.
Слайд 60Графы нашли применение во всех отраслях научных знаний физики, биологии, химии,
истории, прикладной математике , экономике,
программировании, логике, при решении комбинаторных задач, в строительстве, архитектуре, рекламе.
В наше время теория графов приобретает все возрастающий интерес у специалистов самых различных областей науки и техники.
программировании, логике, при решении комбинаторных задач, в строительстве, архитектуре, рекламе.
В наше время теория графов приобретает все возрастающий интерес у специалистов самых различных областей науки и техники.
.
Слайд 61СПИСОК ЛИТЕРАТУРЫ:
1. М. В. Ткачева, Домашняя математика: Кн. для учащихся 7
кл. общеобразоват. учреждений, М.: Просвещение, 1994.
2. В. Волина, «Праздник числа (Занимательная математика для детей)», Книга для учащихся и родителей, Москва, «Знание», 1993.
3. И.Депман, «Рассказы о математике», Детгиз, Ленинград, 1954.
4. Я. И. Перельман, Занимательная алгебра. Занимательная геометрия, М.: ООО «Издательство АСТ», 2002.
5. И. И. Баврин, Е. А. Фридус, Старинные задачи: Кн. для учащихся, М.: «Просвещение», 1994.
6. Болл У., Коксетер Г., Математические эссе и развлечения. Пер. с англ. Под ред. с предисл. и примеч. И. М. Яглома. – М.: Мир, 1986.
2. В. Волина, «Праздник числа (Занимательная математика для детей)», Книга для учащихся и родителей, Москва, «Знание», 1993.
3. И.Депман, «Рассказы о математике», Детгиз, Ленинград, 1954.
4. Я. И. Перельман, Занимательная алгебра. Занимательная геометрия, М.: ООО «Издательство АСТ», 2002.
5. И. И. Баврин, Е. А. Фридус, Старинные задачи: Кн. для учащихся, М.: «Просвещение», 1994.
6. Болл У., Коксетер Г., Математические эссе и развлечения. Пер. с англ. Под ред. с предисл. и примеч. И. М. Яглома. – М.: Мир, 1986.
Продожение…
Слайд 62Список литературы
7.Виленкин Н.Я Комбинаторика
Ж:Наука 1969 год
8. Березина Л. Ю «
Графы и их применения», Ж; Просвещение 1979
9. Мельников О.И «Занимательные задачи по теории графов».
Учебно-метод. Пособие .Минск: Тетра система ,.2001
9. Мельников О.И «Занимательные задачи по теории графов».
Учебно-метод. Пособие .Минск: Тетра система ,.2001
