- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Архитектура вдохновленная математикой
Содержание
- 1. Презентация по математике Архитектура вдохновленная математикой
- 2. Введение Начиная с пирамид и заканчивая сложными
- 3. ВведениеАктуальность нашей работы заключается в том, что
- 4. Цели, задачи и методы.Цели: 1.Исследование взаимосвязи
- 5. Математика для творческого труда архитектора издавна признается
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Таковы: пирамиды Египта
- 10. Парфенон
- 11. София Константинопольская.
- 12. Хотя все мы знаем, что архитектура не
- 13. Слайд 13
- 14. Дом-корзинка
- 15. Кривое здание
- 16. Дом - пианино
- 17. Танцующий дом
- 18. Цели, задачи и методы.Цели: 1.Исследование взаимосвязи
- 19. Этот креатив просто взрывает мозг - смотря
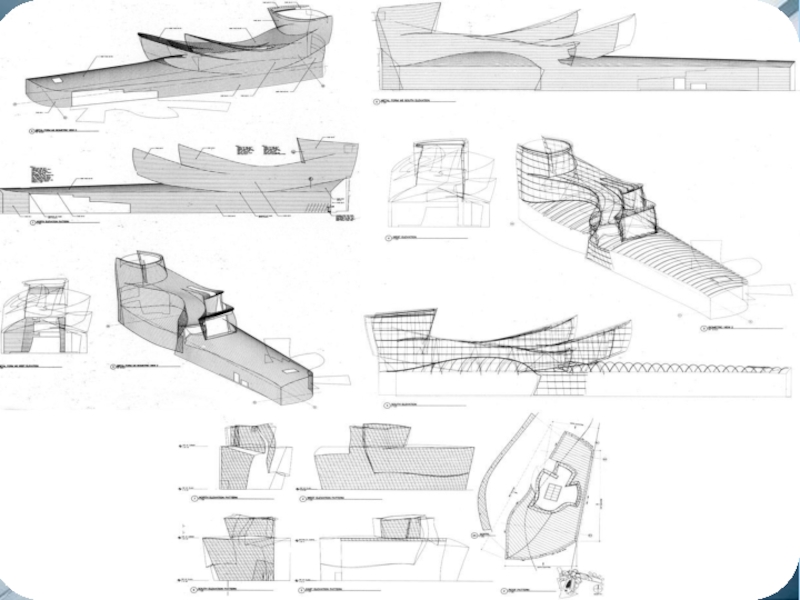
- 20. Museum Bilbao Музей построен по принципу антисимметрии,
- 21. Ярчайший пример - Guggenheim Museum Bilbao
- 22. Слайд 22
- 23. Сиднейский Оперный театр.
- 24. Архитектор выполнил крышу, которая выглядит как открытые
- 25. Слайд 25
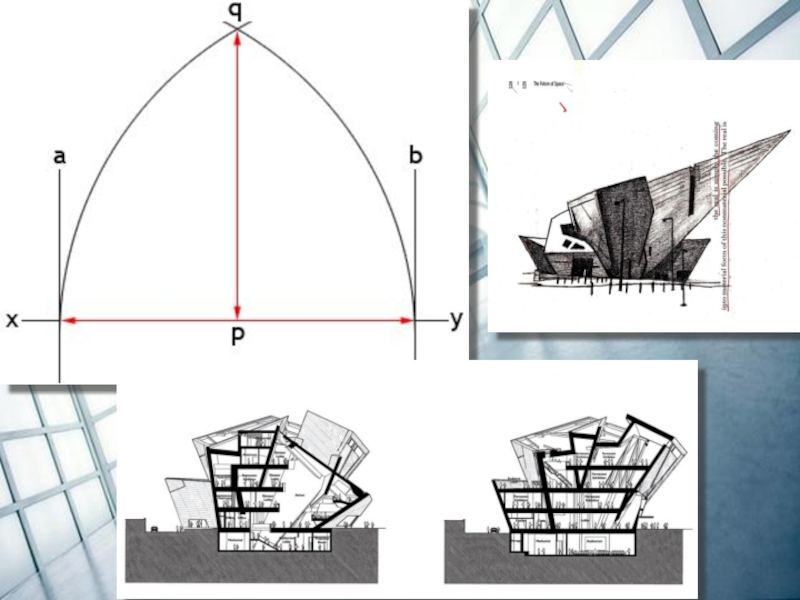
- 26. Музей искусств в Денвере
- 27. Музей искусств в ДенвереЯркий пример ассиметрии. При
- 28. Слайд 28
- 29. Кубические дома в Роттердаме. Спроектированный в 1984
- 30. Кубические дома в Роттердаме
- 31. Слайд 31
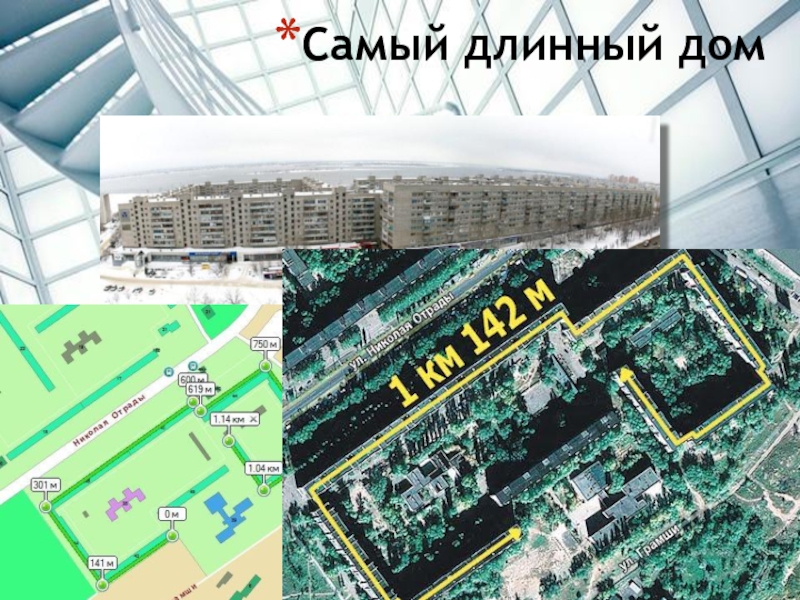
- 32. Самый длинный дом
- 33. Найдите 3 отличия
- 34. Слайд 34
- 35. Слайд 35
- 36. Дома-перевертыши
- 37. Слайд 37
- 38. Слайд 38
- 39. Слайд 39
- 40. Слайд 40
- 41. Слайд 41
- 42. Слайд 42
Слайд 2Введение
Начиная с пирамид и заканчивая сложными конструкциями современного дизайна, архитектура
Используя математику, мы можем понять проявление архитектурного пути далеко за пределами простых измерений. С помощью математики могут быть объяснены такие аспекты, как пропорция и симметрия. Архитекторы, сочетая математику и современные технологии, могут создавать инновационные формы
Хотя все мы знаем, что архитектура не существовала бы без использования математики, мы редко задумываемся о сложности и абстрактности математических уравнений, которые играют определяющую роль в некоторых из самых уникальных зданий мира.
«Прошли века, но роль геометрии не изменилась. Она по-прежнему остается грамматикой архитектора»
Ле Корбюзь
Слайд 3Введение
Актуальность нашей работы заключается в том, что архитектурные объекты являются неотъемлемой
Гипотеза: все здания, которые нас окружают – это геометрические фигуры. Объект исследования: архитектура зданий. Предмет исследования: взаимосвязь архитектуры и геометрии.
Слайд 4Цели, задачи и методы.
Цели:
1.Исследование взаимосвязи геометрии и архитектуры.
2.Развитие познавательного
Задачи: 1. Показать важность применения математики в архитектуре 2. Составить математические задания относительно представленных объектов, с целью их решения 3. Изучить литературу о взаимосвязи геометрии и архитектуры. 4. Рассмотреть геометрические формы в разных архитектурных стилях, и как гарант прочности конструкций. 5. Рассмотреть наиболее интересные архитектурные сооружения и выяснить, какие геометрические формы в них встречаются. Методы исследования : наблюдение, фотографии, изучение и анализ теоретических сведений по данному вопросу.
Слайд 5Математика для творческого труда архитектора издавна признается чем-то очень важным, необходимым
Слайд 12Хотя все мы знаем, что архитектура не существовала бы без использования
Слайд 18Цели, задачи и методы.
Цели:
1.Исследование взаимосвязи математики и архитектуры.
2.Развитие познавательного
Задачи: 1. Показать важность применения математики в архитектуре 2. Составить математические задания относительно представленных объектов, с целью их решения 3. Изучить литературу о взаимосвязи математики и архитектуры. 4. Рассмотреть геометрические формы в разных архитектурных стилях, и как гарант прочности конструкций. 5. Рассмотреть наиболее интересные архитектурные сооружения и выяснить, какие геометрические формы в них встречаются. Методы исследования : наблюдение, фотографии, изучение и анализ теоретических сведений по данному вопросу.
Слайд 19Этот креатив просто взрывает мозг - смотря на здание, что-то меняется
Кажется, никакая математика невозможна описать творческий полет мысли архитекторов.
Я задумалась, а всегда ли нужны эти сложные и казалось бы абстрактные математические закономерности?
Может стоит благополучно забыть даже те азы алгебры, геометрии, которые мы получаем в школе?
Цель моей работы: доказать определяющую роль математики в архитектуре самых уникальных зданий мира.
Этот креатив просто взрывает мозг - смотря на здание, что-то меняется в собственном воображении, и затем обычные дома выглядят какими - то неправильными.
Кажется, никакая математика невозможна описать творческий полет мысли архитекторов.
Я задумалась, а всегда ли нужны эти сложные и казалось бы абстрактные математические закономерности?
Может стоит благополучно забыть даже те азы алгебры, геометрии, которые мы получаем в школе?
Цель моей работы: доказать определяющую роль математики в архитектуре самых уникальных зданий мира.
Слайд 20Museum Bilbao
Музей построен по принципу антисимметрии, т.е. полного отсутствия симметрии
Слайд 24
Архитектор выполнил крышу, которая выглядит как открытые паруса. Утзон хотел придумать
Слайд 27
Музей искусств в Денвере
Яркий пример ассиметрии. При взгляде на здание кажется,
Слайд 29Кубические дома в Роттердаме.
Спроектированный в 1984 году архитектором-новатором Пиетом Бломом, ряд
Рядом с Кубиками возвышается еще одно детище Блома – высотный жилой дом «Карандаш», выполненный в том же стиле, только в виде заточенного карандаша.