- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике (5 класс): Комбинаторные задачи
Содержание
- 1. Презентация по математике (5 класс): Комбинаторные задачи
- 2. Слайд 2
- 3. Задачи, решая которые приходится составлять различные комбинации
- 4. Задача№1.Сколько трехзначных чисел можно составить из цифр
- 5. Проблемный вопрос: Может ли нам комбинаторика помочь в реальной жизни?
- 6. Слайд 6
- 7. Флаги стран Европы, где встречаются три цвета: белый, синий, красный.ФЛАГ РОССИИ
- 8. Рассмотрим задачу.Перед Вами полоски белого, синего
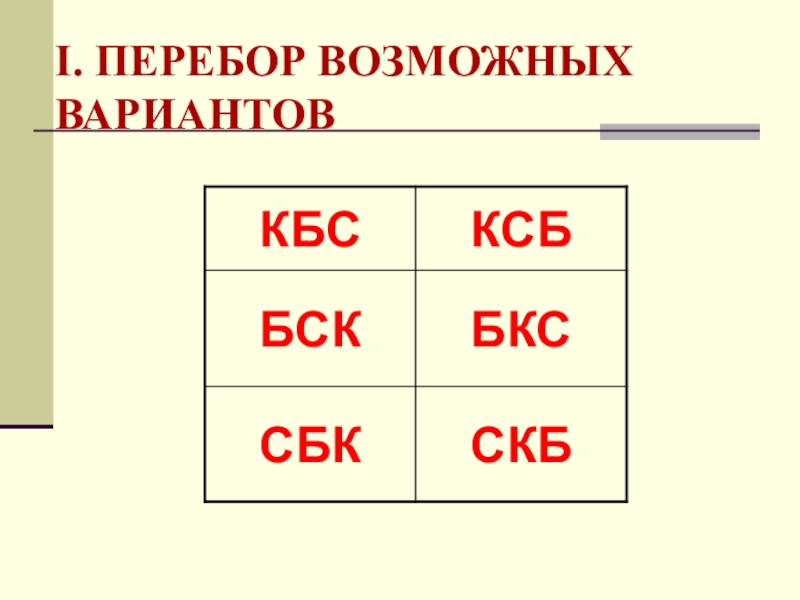
- 9. I. Перебор возможных вариантов
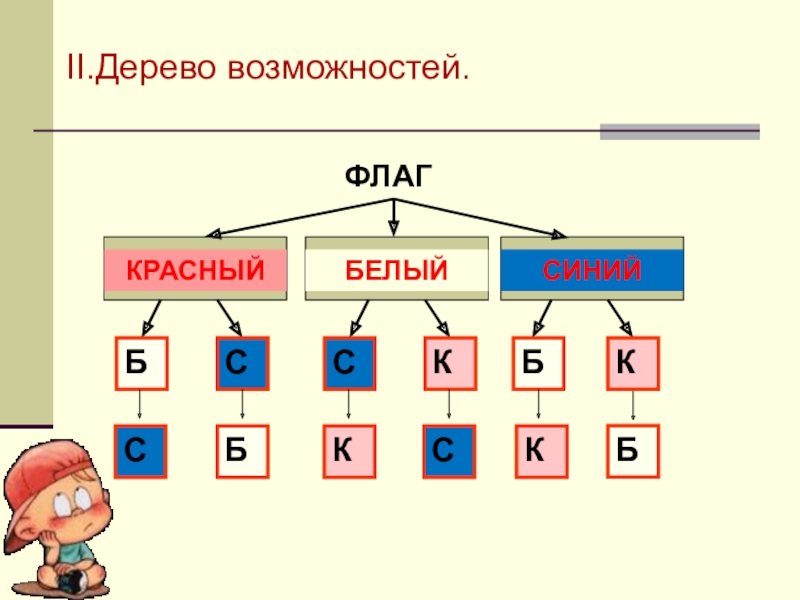
- 10. КРАСНЫЙСБСКБКБЕЛЫЙСИНИЙСБКСКБФЛАГII.Дерево возможностей.
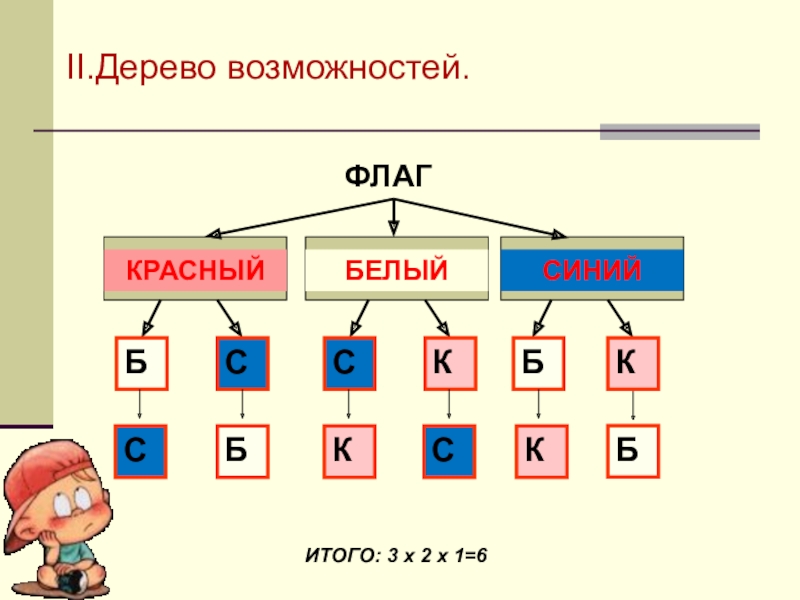
- 11. КРАСНЫЙСБСКБКБЕЛЫЙСИНИЙСБКСКБФЛАГII.Дерево возможностей.ИТОГО: 3 х 2 х 1=6
- 12. III. Правило умножения:если первый элемент в комбинации
- 13. Задача№1.Сколько трехзначных чисел можно составить из цифр
- 14. Проведенный перебор вариантов проиллюстрируем на схеме называемой
- 15. Выпишем все такие числа.Пусть на первом месте
- 16. Проблемный вопрос: Может ли нам комбинаторика помочь в реальной жизни?
- 17. Области применения
- 18. Области применения
- 19. Вывод:Комбинаторика повсюду.Комбинаторика везде.Комбинаторика вокруг нас.
- 20. ПРАВИЛА НАПИСАНИЯ СИНКВЕЙНА:1 строчка – одно слово
Слайд 2
1. Познакомить с комбинаторными задачами.
2. Научить решать простейшие задачи с помощью правила умножения(«Основное правило комбинаторики»).
Слайд 3Задачи, решая которые приходится составлять различные комбинации из конечного числа элементов
Раздел математики, в котором рассматривают
такие задачи, называют
комбинаторикой.
Комбинаторика (от латинского combinare)
означает "соединять, сочетать".
комбинаторных.
Слайд 4Задача№1.
Сколько трехзначных чисел можно составить из цифр 1,3,5,7, используя в записи
Слайд 8
Рассмотрим задачу.
Перед Вами полоски белого, синего и красного цвета. Сколько стран
Слайд 12III. Правило умножения:
если первый элемент в комбинации можно выбрать а способами,
Слайд 13Задача№1.
Сколько трехзначных чисел можно составить из цифр 1,3,5,7, используя в записи
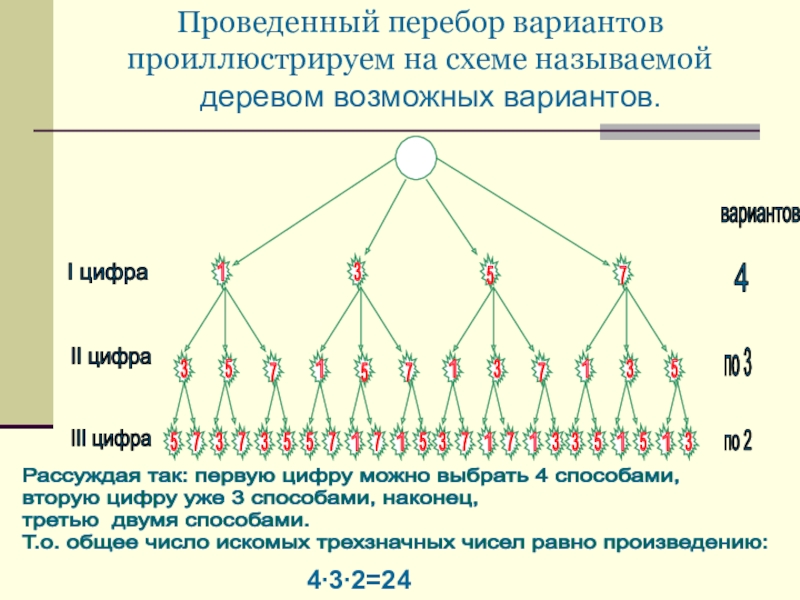
Слайд 14Проведенный перебор вариантов проиллюстрируем на схеме называемой
Рассуждая так: первую цифру
вторую цифру уже 3 способами, наконец,
третью двумя способами.
Т.о. общее число искомых трехзначных чисел равно произведению:
деревом возможных вариантов.
4∙3∙2=24
Слайд 15Выпишем все такие числа.
Пусть на первом месте стоит:
цифра 1, получим
135, 137, 153, 157, 173,175.
Цифра 3, получим
315, 317, 351, 357, 371, 375.
Цифра 5, получим
513, 517, 531, 537, 571, 573.
Цифра 7, получим
713, 715, 731, 735, 751, 753.
Слайд 17Области применения
учебные заведения ( составление расписаний)
сфера общественного питания (составление меню)
лингвистика (рассмотрение вариантов комбинаций букв)
спортивные соревнования (расчёт количества игр между участниками)
агротехника (размещение посевов на нескольких полях)
география (раскраска карт)
биология (расшифровка кода ДНК)
Слайд 18Области применения
химия (анализ возможных связей между химическими элементами)
экономика (анализ вариантов купли-продажи акций) азартные игры (подсчёт частоты выигрышей)
криптография (разработка методов шифрования)
доставка почты (рассмотрение вариантов пересылки)
военное дело (расположение подразделений)
Слайд 20ПРАВИЛА НАПИСАНИЯ СИНКВЕЙНА:
1 строчка – одно слово –тема, обычно существительное.
2 строчка
3 строчка – три слова (глаголы). Действия, относящиеся к теме.
4 строчка – четыре слова – предложение. Фраза, которая показывает отношение автора к теме в 1-ой строчке.
5 строчка – одно слово – ассоциация, синоним, который повторяет суть темы в 1-ой строчке, обычно существительное.
Синквейн.