- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по истории математики Математика Древней Греции
Содержание
- 1. Презентация по истории математики Математика Древней Греции
- 2. При изучении истории любой науки можно проследить
- 3. В периодизации истории математики, которую дал академик
- 4. 1) период зарождения математики до VI-V века
- 5. I период
- 6. Начало периода зарождения математики неизвестно. О точном
- 7. Основная черта II периода - появление доказательства.
- 8. Греки выдвинули тезис «Числа правят миром». Или,
- 9. Источники Бо́льшая часть античных сочинений по математике
- 10. Начиная с VII в. до н.э. в
- 11. Начальный период VI в. до н.э. Подготовила презентацию: Корецкая Виктория
- 12. Вплоть до VI века до н. э. греческая
- 13. Счётная доска (абак) с камушками.
- 14. В VI веке до н. э. начинается «греческое
- 15. Слайд 15
- 16. Фалес, богатый купец, хорошо изучил вавилонскую математику
- 17. Фалес из Милета………В области математики переход научных
- 18. Слайд 18
- 19. Зачинатель и родоначальник греческой философии и науки.
- 20. Фалес определял высоту предмета по его
- 21. Слайд 21
- 22. Счет при помощи камушек.
- 23. Спасибо за внимание )))
- 24. Пифагорейская школа VI-Vв. до н.э.«Все вещи — суть числа». Пифагор
- 25. Пифагор Самосский (ок. 580 — ок. 500г.
- 26. Пифагор, основатель школы — личность легендарная, и достоверность
- 27. Многие достижения, приписываемые Пифагору, вероятно, на самом
- 28. Пифагорейцы были уверены, что «элементы чисел являются
- 29. Они построили общую теорию дробей (теория рациональных
- 30. Первой трещиной в пифагорейской модели
- 31. Следствием этого открытия стал переворот в соотношении
- 32. Школа ПифагораШкола была основана Пифагором и просуществовала
- 33. Первый этап Пифагор обычно отправлял кандидата обратно,
- 34. Афоризмы ПифагораНе делай ничего постыдного ни в
- 35. ДесяткаДесятка может быть выражена суммой первых четырех
- 36. ТетрадаЧисла 1, 2, 3 и 4 составляли
- 37. Идеальное числоСумма чисел, входящих в тетраду, равна
- 38. Справедливость и равенствоСправедливость и равенство пифагорейцы видели
- 39. Число восемь у пифагорейцев символизировало смерть, так
- 40. «Нехорошие числа»Кроме чисел, вызывавших восхищение и преклонение,
- 41. Главным пифагорейским опознавательным знаком был символ здоровья
- 42. 4. V в. до н.э.В V веке
- 43. Зенон Элейский предложил ещё одну тему для
- 44. Ахиллес и черепахаДопустим, Ахиллес бежит в десять
- 45. Афинская школа – Академия Платона V-IV в. до н.э.
- 46. ПЛАТОН
- 47. ЕВДОКС
- 48. III в. до н.э. Евклид, Архимед, Апполоний.
- 49. Евклид. Древнегреческий математик, автор первого из
- 50. После завоеваний Александра Македонского научным центром древнего
- 51. Архимед.Древнегреческий математик, физик и инженер из Сиракуз. Сделал множество открытий в геометрии. Заложил основы механики, гидростатики, автор ряда важных изобретений.
- 52. Архимед – вершина научной мысли древнего мира.
- 53. Аполлоний Пергский.Древнегреческий математик, один из трёх (наряду с Евклидом иАрхимедом) великих геометров античности, живших в III веке до н. э.
- 54. Аполлоний Пергский – автор глубокого исследования конических
- 55. Аполлоний Пергский наряду с Архимедом и Евклидом
- 56. Спасибо за внимание!
- 57. В деятельности Евклида, Аполлония Пергского и особенно
- 58. Среди немногочисленных достижений:известная формула Герона для площади
- 59. ЗаключениеГреческая математика поражает прежде всего красотой и
- 60. 1.Что появилось в математике Древней Греции, чего не было в период зарождения математики?
- 61. Доказательство
- 62. 2. Что такое абак?
- 63. Счётная доска с камушками
- 64. Откуда пришли начальные математические знания в Древнюю Грецию?
- 65. Из Древнего Египта и Древнего Вавилона.
- 66. Кто посвятил свою деятельность тезису «Числа правят миром»?
- 67. Пифагорейцы
- 68. Какое название носит главный труд Евклида?
- 69. «Начала»
- 70. Кто из древнегреческих учёных мастерски владел методами, связанными с интегральными и дифференциальными исследованиями?
- 71. Архимед
- 72. Где произошёл расцвет математики после упадка развития математики в Древней Греции?
- 73. В странах ислама – арабская математика.
Слайд 2При изучении истории любой науки можно проследить развитие (генезис) идей, как
Слайд 3В периодизации истории математики, которую дал академик А.Н.Колмагоров, выделяются следующие периоды:
Андрей
Слайд 41) период зарождения математики до VI-V века до н.э. 2) математика постоянных
Слайд 5I период
! (наука основана на доказательстве – ! матем. переем величин! совр. матем
! дедуктивная математика) ! !
Зарождение математики! Математика пост. величин ! !
__________________VI-Vв. до н.э. ______0________________XVI-XVII в____________2 полов________
XIXв
Слайд 6Начало периода зарождения математики неизвестно. О точном появлении математики мы можем
Главные достижения этого периода – возникновение абстрактных понятий (число, фигура, площадь, объём) и замена конкретных условий задач общими – это первичная форма создания алгоритмов.
Слайд 7Основная черта II периода - появление доказательства. Вся элементарная математика развилась
Слайд 8Греки выдвинули тезис «Числа правят миром». Или, как сформулировал эту же
Греки проверили справедливость этого тезиса в тех областях, где сумели: астрономия, оптика, музыка, геометрия, позже — механика. Всюду были отмечены впечатляющие успехи: математическая модель обладала неоспоримой предсказательной силой. Одновременно греки создали методологию математики и завершили превращение её из свода полуэвристических алгоритмов в целостную систему знаний. Основой этой системы впервые стал дедуктивный метод, показывающий, как из известных истин выводить новые, причём логика вывода гарантирует истинность новых результатов. Дедуктивный метод также позволяет выявить неочевидные связи между понятиями, научными фактами и областями математики.
Слайд 9Источники Бо́льшая часть античных сочинений по математике не дошла до наших дней
Слайд 10Начиная с VII в. до н.э. в Древней Греции начали возникать
Ионийская школа (основатель - Фалес Милетский) VII-VI в. до н.э.
Пифагорейская школа (основатель – Пифагор) VI-V в. до н.э.
Афинская школа (основатель Платон) V-IV в. до н.э.
Александрийская школа III-II в. до н.э.
Слайд 12
Вплоть до VI века до н. э. греческая математика ничем не выделялась.
Позднее (начиная с V века до н. э.) была принята алфавитная нумерация— первые 9 букв греческого алфавита обозначали цифры от 1 до 9, следующие 9 букв — десятки, остальные — сотни. Чтобы не спутать числа и буквы, над числами рисовали чёрточку. Числа, большие 1000, записывали позиционно, помечая дополнительные разряды специальным штрихом (внизу слева). Специальные пометки позволяли изображать и числа, большие 10 000.
Слайд 14В VI веке до н. э. начинается «греческое чудо»: появляются сразу две
Слайд 16Фалес, богатый купец, хорошо изучил вавилонскую математику и астрономию — вероятно, во
Слайд 17Фалес из Милета………
В области математики переход научных знаний из Египта в
Легенда рассказывает о том, что Фалес привел в изумление египетского царя Амазиса, измерив высоту одной из пирамид по величине отбрасываемой ею тени.
Слайд 19Зачинатель и родоначальник греческой философии и науки. Считается, что Фалес первым
вертикальные углы равны;
треугольники с равной одной стороной и равными углами, прилегающими к ней, равны;
углы при основании равнобедренного треугольника равны;
диаметр делит круг пополам;
угол, вписанный в
полуокружность, всегда
будет прямым.
Слайд 20 Фалес определял высоту предмета по его тени, расстояния до кораблей,
Слайд 25Пифагор Самосский (ок. 580 — ок. 500г. до н. э.) —
Слайд 26Пифагор, основатель школы — личность легендарная, и достоверность дошедших
до
невозможно. Пифагор родился на острове
Самос.
Видимо, он, как и Фалес, много путешествовал
и тоже учился у египетских и вавилонских
мудрецов. Вернувшись около 530 г. до н. э. в
Великую Грецию (район южной Италии) он
основал нечто вроде тайного духовного
ордена. Именно он выдвинул тезис
«Числа правят миром», и с исключительной
энергией занимался его обоснованием. В начале V в. до н. э., после неудачного политического выступления, пифагорейцы были изгнаны из Южной Италии, и союз прекратил свое существование, однако популярность учения от рассеяния только возросла. Пифагорейские школы появились в Афинах, на островах и в греческих колониях, а их математические знания, строго оберегаемые от посторонних, сделались общим достоянием.
Слайд 27Многие достижения, приписываемые Пифагору, вероятно, на самом деле являются заслугой его
Слайд 28Пифагорейцы были уверены, что «элементы чисел являются элементами всех вещей… и
Слайд 29Они построили общую теорию дробей (теория рациональных чисел) (понимаемых как отношения
Ранние пифагорейцы полагали, что отношение любых 2-х отрезков можно выразить с помощью отношения чисел. Таким образом геометрию они пытались свести к арифметике.
Слайд 30Первой трещиной
в пифагорейской модели мира стало ими же
Слайд 31Следствием этого открытия стал переворот в соотношении арифметики и геометрии. Если
числам. Этот этап развития алгебры называют геометрической
алгеброй.
Слайд 32Школа Пифагора
Школа была основана Пифагором и просуществовала до начала IV в.
Прием в школу проходил
в несколько этапов
Слайд 33Первый этап
Пифагор обычно отправлял кандидата обратно, советуя повременить и прийти
За первым этапом
следовало ещё 4
многолетних непростых
этапа.
Слайд 34Афоризмы Пифагора
Не делай ничего постыдного ни в присутствии других, ни втайне.
Для познания нравов какого ни есть народа старайся прежде изучить его язык.
Если можешь быть орлом, не стремись стать первым среди галок.
Во время гнева не должно ни говорить, ни действовать.
Жизнь подобна игрищам: иные приходят на них состязаться, иные — торговать, а самые счастливые — смотреть.
Как ни коротки слова «да» и «нет», все же они требуют самого серьезного размышления.
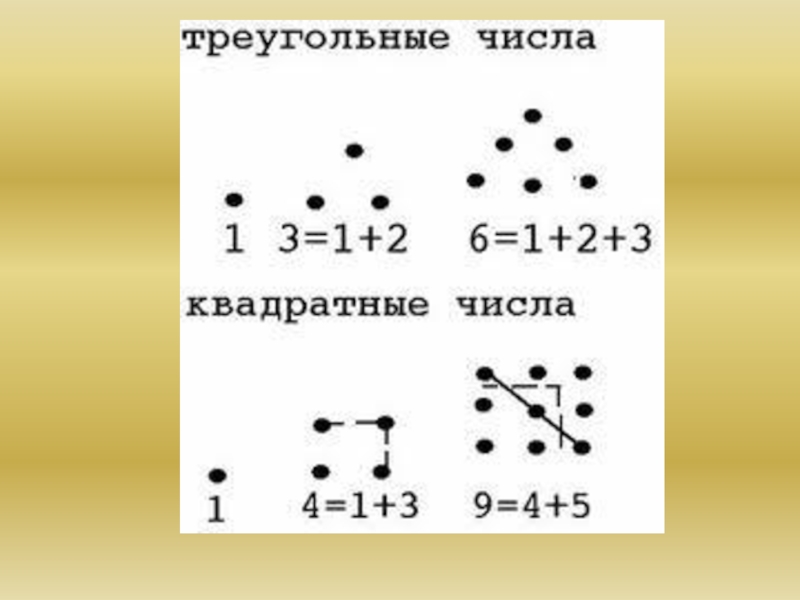
Слайд 35Десятка
Десятка может быть выражена суммой первых четырех чисел (1+2+3+4=10), где единица
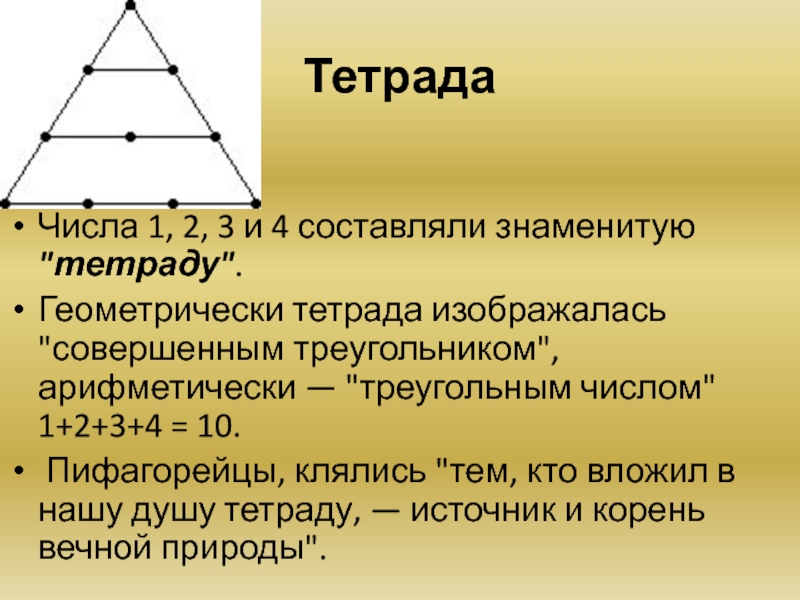
Слайд 36Тетрада
Числа 1, 2, 3 и 4 составляли знаменитую "тетраду".
Геометрически тетрада
Пифагорейцы, клялись "тем, кто вложил в нашу душу тетраду, — источник и корень вечной природы".
Слайд 37Идеальное число
Сумма чисел, входящих в тетраду, равна десяти, именно поэтому десятка
Поскольку число десять — идеальное, рассуждали они, на небе должно быть ровно десять планет. Надо заметить, что тогда были известны лишь Солнце, Земля и пять планет.
Слайд 38Справедливость и равенство
Справедливость и равенство пифагорейцы видели в квадрате числа.
Символом
9*2=18 1+8=9;
7*9=63 6+3=9;
11*9=99 9+9=18 1+8=9;
25*9= 225 2+2+5=9.
Слайд 39Число восемь у пифагорейцев символизировало смерть, так как кратные восьми имеют
8*2=16 1+6=7;
8*3=24 2+4=6;
8*4=32 3+2=5;
8*5+40 4+0=4;
8*6=48 4+8=12 1+2=3
Слайд 40«Нехорошие числа»
Кроме чисел, вызывавших восхищение и преклонение, у пифагорейцев были и
Знаменитое число тринадцать — чертова дюжина
Число семнадцать, вызывавшее особое отвращение у пифагорейцев.
Слайд 41Главным пифагорейским опознавательным знаком был символ здоровья – пентаграмма или пифагорейская
Нарисованная пентаграмма была тайным знаком, по которому пифагорейцы узнавали друг друга. В средние века считалось, что пентаграмма “предохраняет” от “нечистой силы
Слайд 424. V в. до н.э.
В V веке до н. э. появились три классические
Слайд 43Зенон Элейский предложил ещё одну тему для многовековых размышлений математиков. Он
Слайд 44Ахиллес и черепаха
Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха,
Здесь предполагается, что пространство и время не имеют предела делимости.
Летящая стрела
Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.
Слайд 46ПЛАТОН
Девиз академии Платона был:
"Не
Уже к началу IV века до н. э. греческая математика далеко опередила всех своих учителей, и её бурное развитие продолжалось. В 389 году до н. э. Платон основывает в Афинах свою школу - знаменитую Академию. Математиков, присоединившихся к Академии, можно разделить на две группы: на тех, кто получил своё математическое образование вне Академии, и на учеников Академии. К числу первых принадлежали Теэтет Афинский, Архит Тарентский и позднее Евдокс Книдский; к числу вторых - Амикл из Гераклеи, братья Менехм и Динострат.
Сам Платон конкретных математических исследований не вёл, но опубликовал глубокие рассуждения по философии и методологии математики. А ученик Платона, Аристотель, оставил бесценные для нас записки по истории математики.
Слайд 47 ЕВДОКС
Евдокс Книдский (ок. 408 – ок. 355 до н.э.) – гениальный математик, астроном, географ, врач, философ, оратор. Обогатил математику выдающимися открытиями, всю глубину которых ученые оценили лишь в конце XIX – начале XX в. Он безукоризненно разработал строгую теорию отношений, явившуюся первой аксиоматической теорией действительного числа, чтобы избежать актуально бесконечно малых и бесконечно больших величин. Евдокс ввел знаменитую аксиому, вошедшую в математику как аксиома Архимеда. Разработал метод исчерпывания – первое учение о пределах. В основу его была положена лемма, позволяющая находить пределы широкого класса последовательностей.
Слайд 49Евклид.
Древнегреческий математик, автор первого из дошедших до нас теоретических
Слайд 50После завоеваний Александра Македонского научным центром древнего мира становится Александрия Египетская.
Учёные Александрии объединили вычислительную мощь и древние знания вавилонских и египетских математиков с научными моделями эллинов. Значительно продвинулись плоская и сферическая тригонометрия, статика и гидростатика, оптика, музыка и др. Эратосфен уточнил длину меридиана и изобрёл своё знаменитое «решето». В истории математики известны три великих геометра древности, и прежде всего — Евклид с его «Началами». Тринадцать книг Начал — основа античной математики, итог её 300-летнего развития и база для дальнейших исследований. Влияние и авторитет этой книги были огромны в течение двух тысяч лет.
Слайд 51Архимед.
Древнегреческий математик, физик и инженер из Сиракуз. Сделал множество открытий в геометрии. Заложил основы механики,
гидростатики, автор ряда важных
Слайд 52Архимед – вершина научной мысли древнего мира. Архимед родился в 287
Слайд 53Аполлоний Пергский.
Древнегреческий математик, один из трёх (наряду с Евклидом и
Архимедом) великих геометров античности,
Слайд 54Аполлоний Пергский – автор глубокого исследования конических сечений – сечения прямоугольного,
Слайд 55Аполлоний Пергский наряду с Архимедом и Евклидом третий из самых выдающихся
«Конические сечения» - яркий пример теории, возникшей из логики развития самой математики и лишь со временем нашедшей практическое применение. Теория конических сечений Апполония нашла применение лишь в XVI – XVII вв., когда Кеплер установил, что планеты Солнечной системы движутся по эллипсам, а Галилей показал, что брошенный камень (снаряд) летит в пустоте по параболе.
Слайд 57В деятельности Евклида, Аполлония Пергского и особенно Архимеда период самостоятельной деятельности
После Аполлония (со II века до н. э.) в античной науке начался спад. Новых глубоких идей не появляется. В 146 году до н. э. Рим захватывает Грецию, а в 31 году до н. э. — Александрию.
Слайд 58Среди немногочисленных достижений:
известная формула Герона для площади треугольника (I век н. э.);
содержательное
завершение геоцентрической модели мира Птолемея (II век н. э.), для чего потребовалась глубокая разработка плоской и сферической тригонометрии.
Необходимо отметить деятельность Паппа Александрийского (III век). Только благодаря ему до нас дошли сведения об античных учёных и их трудах.
На фоне общего застоя и упадка резко выделяется гигантская фигура Диофанта— последнего из великих античных математиков, «отца алгебры». Главный труд Диофанта– “Арифметика”, по предположению, состоит из 13 книг. Книга Диофанта “Арифметика” содержала большое количество интересных задач, её изучали математики всех поколений. Книга сохранилась до наших дней. В честь Диофанта назван кратер на Луне.
После III века н. э. александрийская школа просуществовала около 100 лет — приход христианства и частые смуты в империи резко снизили интерес к науке. Отдельные учёные труды ещё появляются в Афинах, но в 529 году Юстиниан закрыл Афинскую академию как рассадник язычества.
Часть учёных переехала в Персию или Сирию и продолжала труды там. От них уцелевшие сокровища античного знания получили учёные стран ислама.
Слайд 59Заключение
Греческая математика поражает прежде всего красотой и богатством содержания. Многие учёные
Первое — греки построили математику как целостную науку с собственной методологией, основанной на чётко сформулированных законах логики.
Второе — они провозгласили, что законы природы постижимы для человеческого разума, и математические модели — ключ к их познанию.