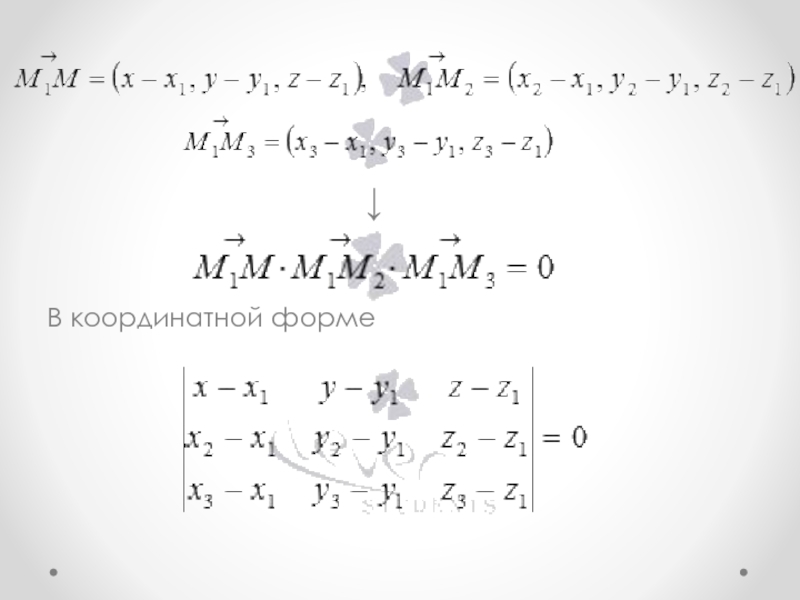- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии УРАВНЕНИЕ ПЛОСКОСТИ
Содержание
- 1. Презентация по геометрии УРАВНЕНИЕ ПЛОСКОСТИ
- 2. Аксиома: через три несовпадающие и не лежащие на одной прямой точки трехмерного пространства проходит единственная плоскость
- 3. Пусть в координатном пространстве Οxyz заданы три точки, не
- 4. Первый способ составления уравнения плоскости, проходящей через
- 5. Так как нормальный вектор плоскости и любой
- 6. После вычисления записанного определителя, станут видны координаты
- 7. Второй способ составления уравнения плоскости, проходящей через
- 8. Слайд 8
- 9. Пример:Напишите уравнение плоскости, которая проходит через три заданные точки
- 10. Первый способ:Вычисляем координаты векторов
- 11. уравнение плоскости, проходящей через точку и имеющей нормальный векторОтвет: – 5x + 30y + 2z – 73
- 12. Второй способ:Уравнение плоскости, проходящей через 3 заданные точки:Из условия задачи:
- 13. Слайд 13
Аксиома: через три несовпадающие и не лежащие на одной прямой точки трехмерного пространства проходит единственная плоскость
Слайд 2Аксиома: через три несовпадающие и не лежащие на одной прямой точки
трехмерного пространства проходит единственная плоскость
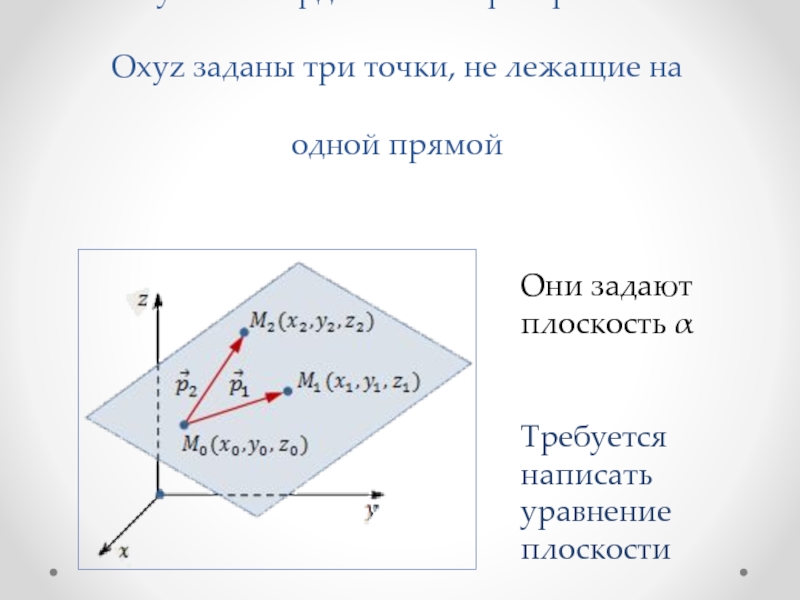
Слайд 3Пусть в координатном пространстве Οxyz заданы три точки, не лежащие на одной прямой
Требуется
написать уравнение плоскости
Они задают плоскость α
Слайд 4Первый способ составления уравнения плоскости, проходящей через три заданные точки
общее уравнение
плоскости вида
задает в системе координат Oxyz плоскость ,
которая проходит через точку ,
а нормальный вектор плоскости имеет координаты
задает в системе координат Oxyz плоскость ,
которая проходит через точку ,
а нормальный вектор плоскости имеет координаты
Слайд 5Так как нормальный вектор плоскости и любой ненулевой вектор этой плоскости
перпендикулярны, то вектор перпендикулярен как вектору , так и вектору
↓
= * ,
Так как
} =>
↓
= * ,
Так как
} =>
Слайд 6После вычисления записанного определителя, станут видны координаты нормального вектора
, и можно записывать требуемое уравнение плоскости, проходящей через три заданные точки.
Слайд 7Второй способ составления уравнения плоскости, проходящей через три заданные точки
Плоскость определена
тогда и только тогда, когда три вектора компланарны
Слайд 11уравнение плоскости, проходящей через точку
и имеющей нормальный вектор
Ответ: – 5x +
30y + 2z – 73