- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Понятие многогранника
Содержание
- 1. Презентация по геометрии Понятие многогранника
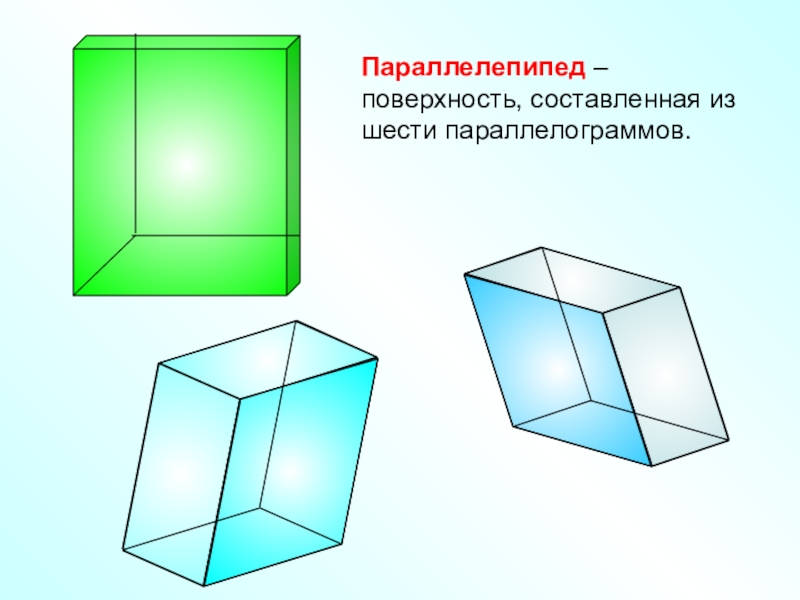
- 2. Параллелепипед – поверхность, составленная из шести параллелограммов.
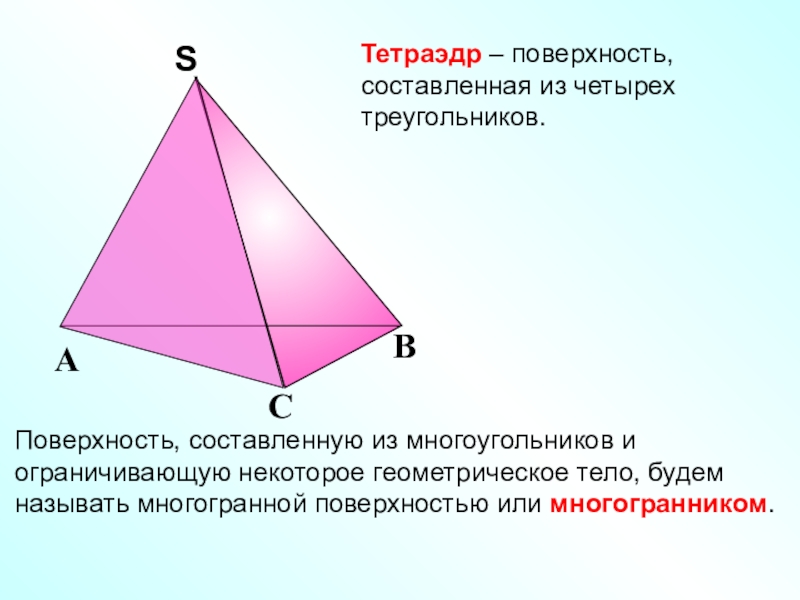
- 3. Тетраэдр – поверхность, составленная из четырех треугольников.
- 4. Октаэдр составлен из восьми треугольников.Многоугольники, из которых
- 5. Прямоугольный параллелепипедМногогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.
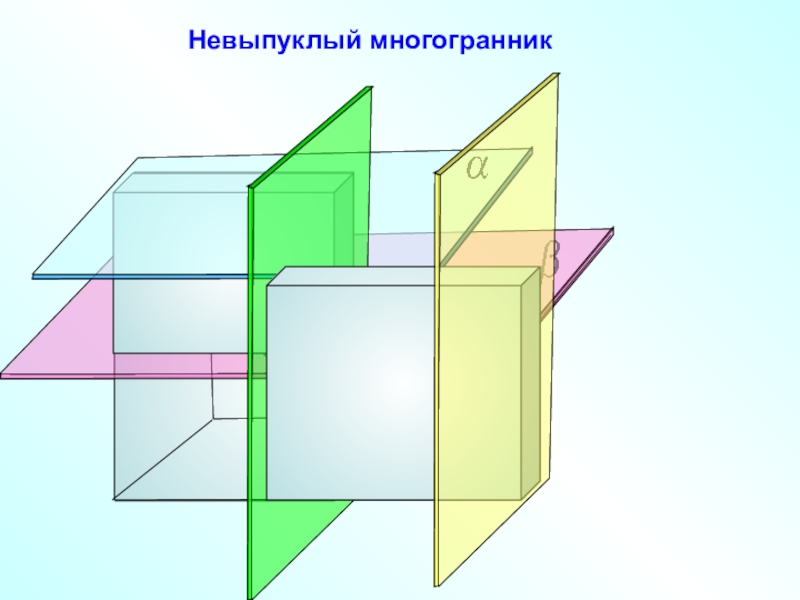
- 6. Невыпуклый многогранник
- 7. Теорема Эйлера: В любом выпуклом многограннике сумма
- 8. ПризмаА1А2АnB1B2BnB3А3Многогранник, составленный из двух равных многоугольников А1А2…Аn
- 9. ПризмаА1А2АnB1B2BnB3А3Отрезки А1В1, А2В2 и т.д. - боковые
- 10. Если боковые ребра перпендикулярны к основаниям, то
- 11. Прямая призма называется правильной, если ее основания
- 12. Площадью полной поверхности призмы называется сумма площадей
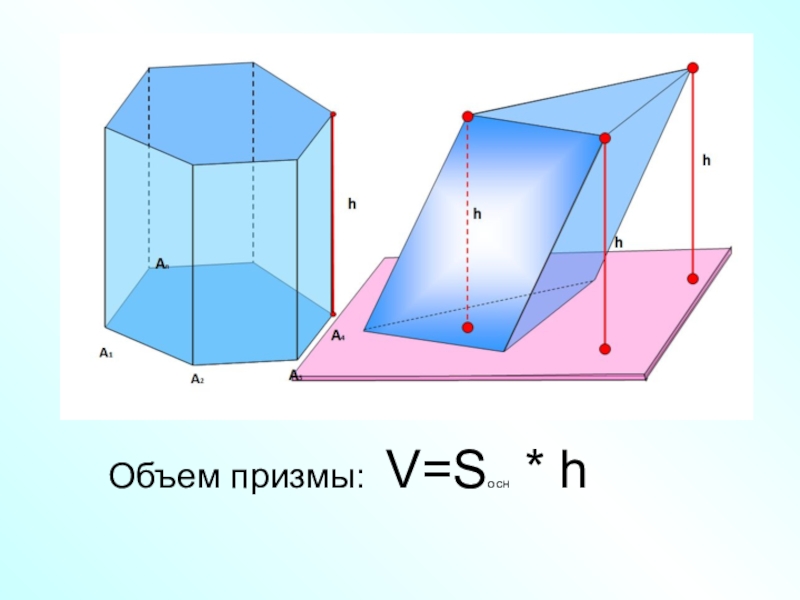
- 13. Объем призмы: V=Sосн * h
Параллелепипед – поверхность, составленная из шести параллелограммов.
Слайд 3Тетраэдр – поверхность, составленная из четырех треугольников.
Поверхность, составленную из многоугольников
и ограничивающую некоторое геометрическое тело, будем называть многогранной поверхностью или многогранником.
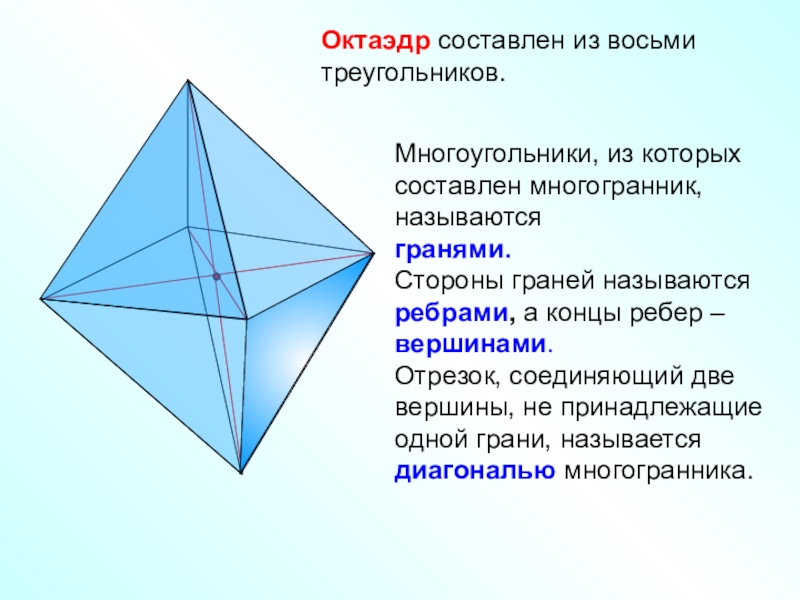
Слайд 4Октаэдр составлен из восьми треугольников.
Многоугольники, из которых составлен многогранник, называются
гранями.
Стороны
граней называются ребрами, а концы ребер – вершинами.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Слайд 5
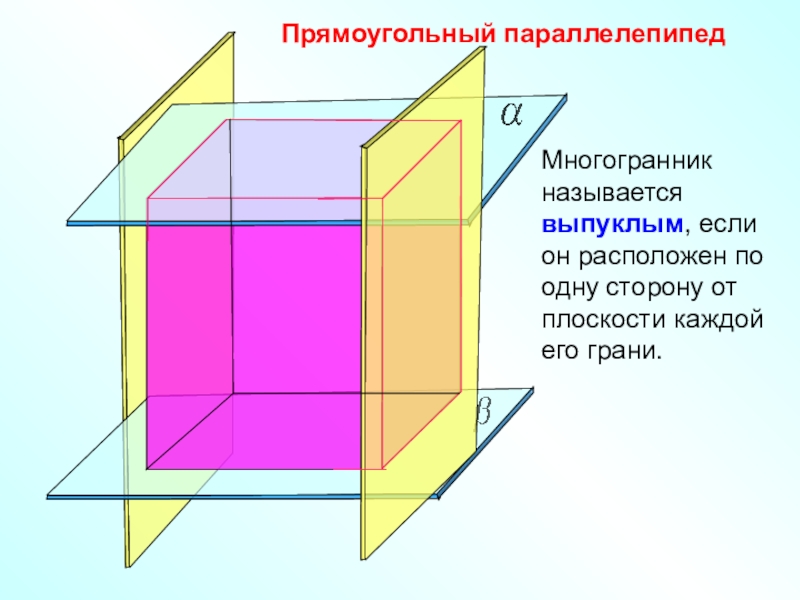
Прямоугольный параллелепипед
Многогранник называется выпуклым, если он расположен по одну сторону от
плоскости каждой его грани.
Слайд 7
Теорема Эйлера: В любом выпуклом многограннике сумма числа граней и числа
вершин больше числа ребер на 2.
Слайд 8
Призма
А1
А2
Аn
B1
B2
Bn
B3
А3
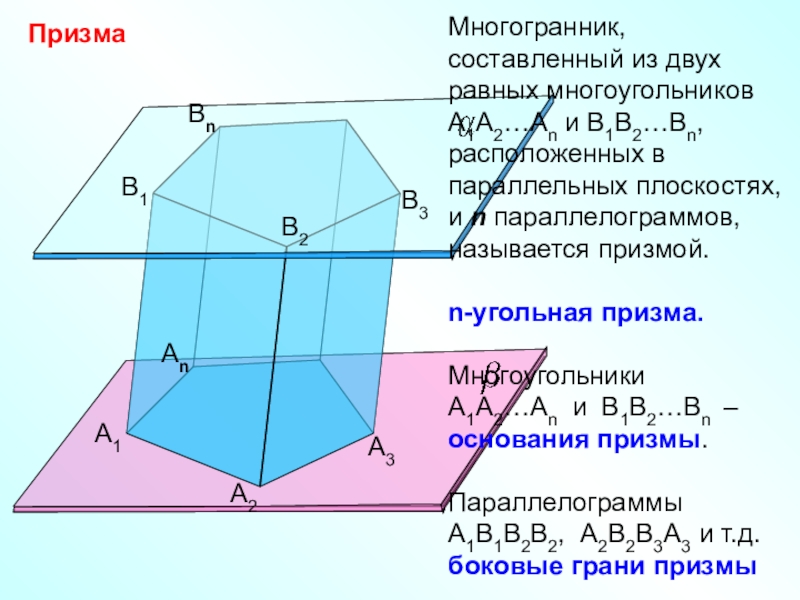
Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn, расположенных в
параллельных плоскостях, и n параллелограммов, называется призмой.
n-угольная призма.
Многоугольники
А1А2…Аn и В1В2…Вn – основания призмы.
Параллелограммы А1В1В2В2, А2В2В3А3 и т.д. боковые грани призмы
n-угольная призма.
Многоугольники
А1А2…Аn и В1В2…Вn – основания призмы.
Параллелограммы А1В1В2В2, А2В2В3А3 и т.д. боковые грани призмы
Слайд 9
Призма
А1
А2
Аn
B1
B2
Bn
B3
А3
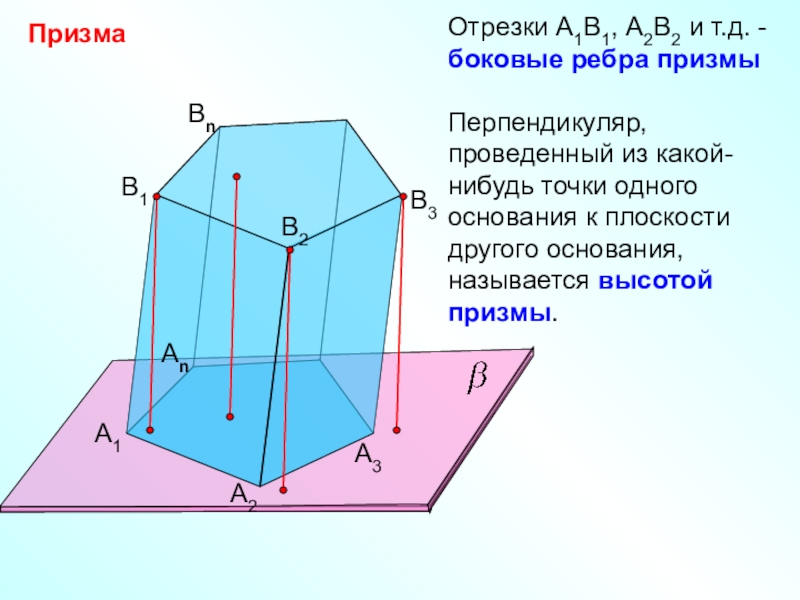
Отрезки А1В1, А2В2 и т.д. -
боковые ребра призмы
Перпендикуляр, проведенный из
какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
Слайд 10
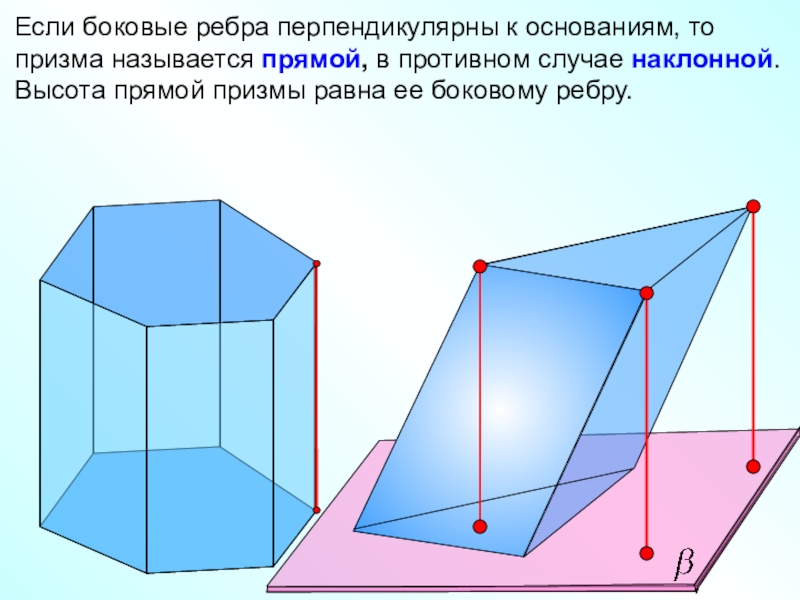
Если боковые ребра перпендикулярны к основаниям, то призма называется прямой, в
противном случае наклонной.
Высота прямой призмы равна ее боковому ребру.
Высота прямой призмы равна ее боковому ребру.
Слайд 11
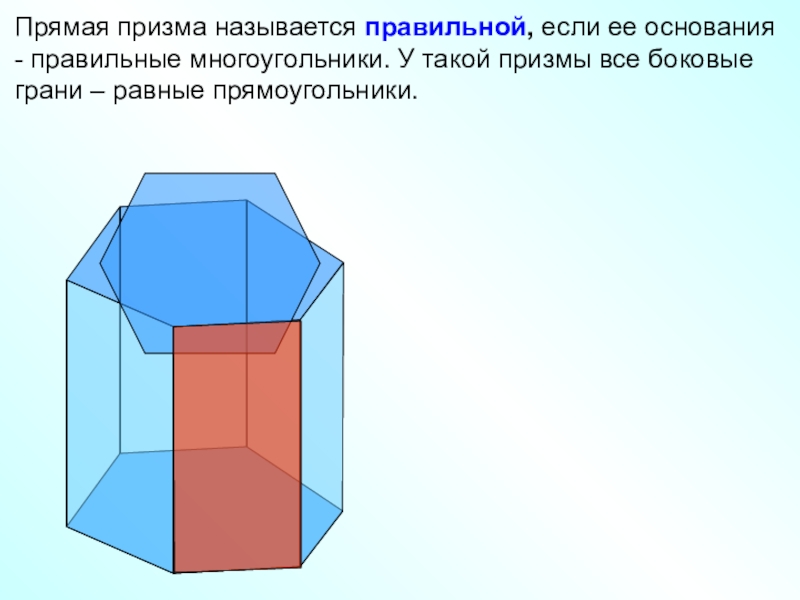
Прямая призма называется правильной, если ее основания - правильные многоугольники. У
такой призмы все боковые грани – равные прямоугольники.
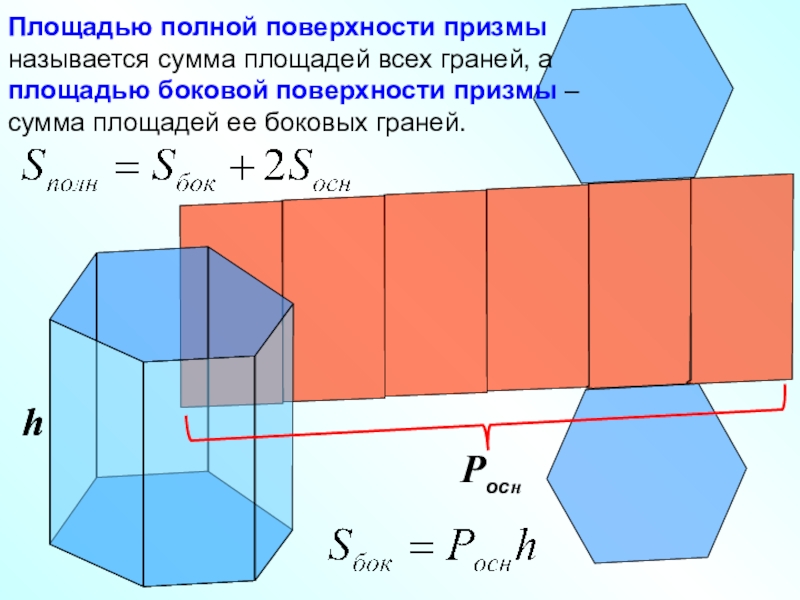
Слайд 12Площадью полной поверхности призмы называется сумма площадей всех граней, а площадью
боковой поверхности призмы – сумма площадей ее боковых граней.
h
h
Pocн