- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии по теме Многогранники
Содержание
- 1. Презентация по геометрии по теме Многогранники
- 2. Домашнее задание:Повторить главы: 8 и
- 3. Многогранник, две грани которого -
- 4. Если боковое ребро призмы перпендикулярно плоскости ее
- 5. Свойства призмы 1. Основания призмы являются равными
- 6. Площадь боковой поверхности прямой призмы
- 7. *Логинова Н.В. МБОУ «СОШ №16»Пирамидой называется
- 8. Боковые грани правильной пирамиды - равнобедренные треугольники,
- 9. *Логинова Н.В. МБОУ «СОШ №16»Свойства правильной
- 10. Объём пирамиды Площадью полной поверхности пирамиды называется
- 11. Проверочная работа1. Определение: а) призмы; б) пирамиды.2.
Слайд 2Домашнее задание:
Повторить главы:
8 и 12 (окружность),
«Считай несчастным тот день и тот час, в который ты не усвоил ничего, и ничего не прибавил к своему образованию»
Я.А.Коменский
*
Логинова Н.В. МБОУ «СОШ №16»
Слайд 3 Многогранник, две грани которого - одноименные многоугольники, лежащие в
Термин “призма” греческого происхождения и буквально означает “отпиленное” (тело).
Многоугольники, лежащие в параллельных плоскостях, называют основаниями призмы, а остальные грани - боковыми гранями.
Поверхность призмы, таким образом, состоит из двух равных многоугольников (оснований) и параллелограммов (боковых граней).
*
Логинова Н.В. МБОУ «СОШ №16»
Слайд 4Если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму
*
Логинова Н.В. МБОУ «СОШ №16»
Если боковое ребро призмы не перпендикулярно плоскости ее основания, то такую призму называют наклонной.
Перпендикуляр к плоскостям оснований, концы которого принадлежат этим плоскостям, называют высотой призмы.
Прямая призма, основанием которой служит правильный многоугольник, называется правильной призмой.
Слайд 5Свойства призмы
1. Основания призмы являются равными многоугольниками.
2. Боковые грани призмы являются
*
Логинова Н.В. МБОУ «СОШ №16»
Слайд 6 Площадь боковой поверхности прямой призмы равна произведению периметра ее
Площадь боковой поверхности призмы равна произведению периметра ее перпендикулярного сечения и длины бокового ребра.
Sбок =Pl
*
Логинова Н.В. МБОУ «СОШ №16»
Sбок =Ph
Объем призмы равен произведению площади её основания на высоту.
V=Sосн h
Площадь поверхности призмы равна сумме площадей боковой поверхности и двум площадям основания.
Sпов= Sбок+2Sосн
Слайд 7*
Логинова Н.В. МБОУ «СОШ №16»
Пирамидой называется многогранник, который состоит из
Треугольники SAB, SBC, SCD, SDA - боковые грани.
SA, SB, SC, SD - боковые ребра пирамиды.
Перпендикуляр SO, опущенный из вершины на основание, называется высотой пирамиды и обозначается h.
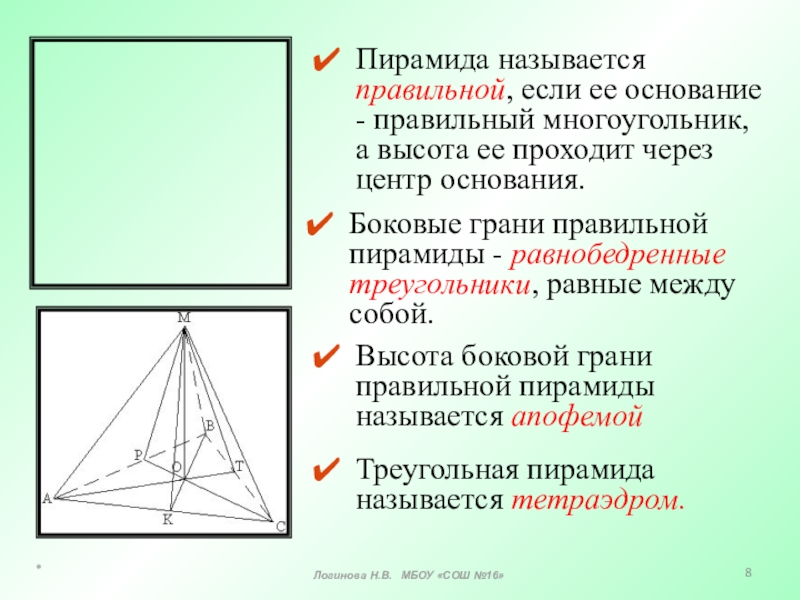
Слайд 8Боковые грани правильной пирамиды - равнобедренные треугольники, равные между собой.
Пирамида
Треугольная пирамида называется тетраэдром.
Высота боковой грани правильной пирамиды называется апофемой
*
Логинова Н.В. МБОУ «СОШ №16»
Слайд 9*
Логинова Н.В. МБОУ «СОШ №16»
Свойства правильной пирамиды
3. В правильной пирамиде
5. Все плоские углы при вершине равны, все плоские углы при основании равны.
1. В правильной пирамиде все двугранные углы при основании равны.
4. Все боковые грани правильной пирамиды равные равнобедренные треугольники.
2. Апофемы правильной пирамиды равны.
Слайд 10Объём пирамиды
Площадью полной поверхности пирамиды называется сумма площадей всех её
Sполн=Sбок+Sосн;
Площадь боковой поверхности пирамиды – сумма площадей её боковых граней;
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
, где m – апофема, Р – периметр основания;
Площадь боковой грани
где m – апофема, а - основание грани;
*
Логинова Н.В. МБОУ «СОШ №16»
Слайд 11Проверочная работа
1. Определение: а) призмы; б) пирамиды.
2. Ответьте на вопрос: а)
б) как называется перпендикуляр к плоскостям оснований призмы, концы которого принадлежат этим плоскостям?
3. Определение правильной: а) призмы; б) пирамиды.
4. Определение: а) тетраэдра; б) наклонной призмы.
5. Формула площади полной поверхности: а) пирамиды; б) призмы.
6. Формула площади боковой поверхности: а) прямой призмы;
б) правильной пирамиды.
7. Формула площади: а) боковой грани пирамиды; б) боковой поверхности наклонной призмы.
8. Формула объема: а) призмы; б) пирамиды.
9. Свойства: а) правильной пирамиды; б) призмы.
10. Задача: а) №1242; б) №1238.
*
Логинова Н.В. МБОУ «СОШ №16»