- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Параллелограмм
Содержание
- 1. Презентация по геометрии Параллелограмм
- 2. Содержание: ОпределениеПервое свойство параллелограммаВторое свойство параллелограммаЗадача Вопросы и задачи Самостоятельная работа
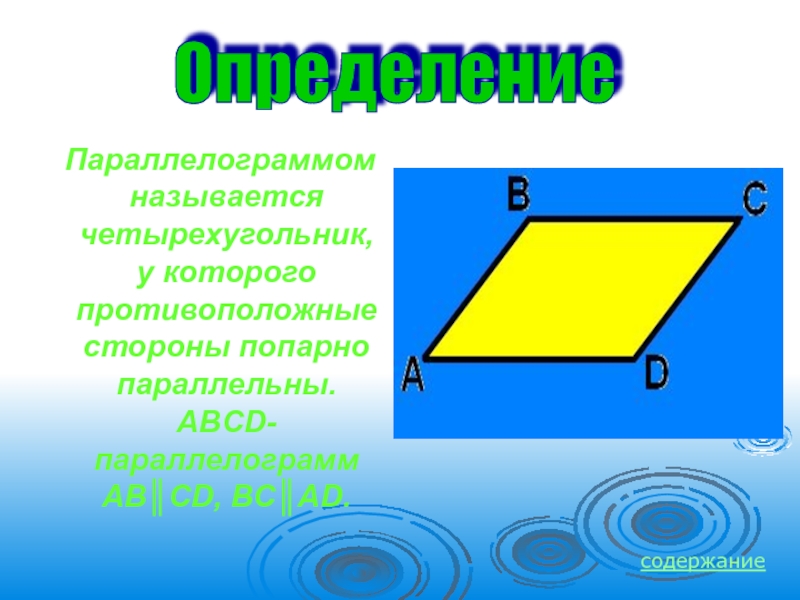
- 3. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны. ABCD-параллелограмм AB║CD, BC║AD.Определение содержание
- 4. Первое свойство параллелограммаДано:ABCD-параллелограммДоказать: AB=CD, AD=DC, ﮮA=ﮮC, ﮮD=ﮮBВ
- 5. Второе свойство параллелограммаДиагонали параллелограмма точкой пересечения делятся
- 6. ЗадачаДокажите, что выпуклый четырехугольник ABCD является параллелограммом,
- 7. Вопросы и задачи:Дайте определение параллелограмма. Является ли
- 8. Самостоятельная работаВариант 1Периметр параллелограмма равен 48 см.Найдите
Слайд 1Параллелограмм
Работа
Учителя математики
МБОУ «Школа №129»
Приволжского района,
Г.Казани
Гинановой С.М.
Слайд 2Содержание:
Определение
Первое свойство параллелограмма
Второе свойство параллелограмма
Задача
Вопросы и задачи
Самостоятельная
Слайд 3 Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны. ABCD-параллелограмм
Определение
содержание
Слайд 4Первое свойство параллелограмма
Дано:
ABCD-параллелограмм
Доказать:
AB=CD, AD=DC, ﮮA=ﮮC,
ﮮD=ﮮB
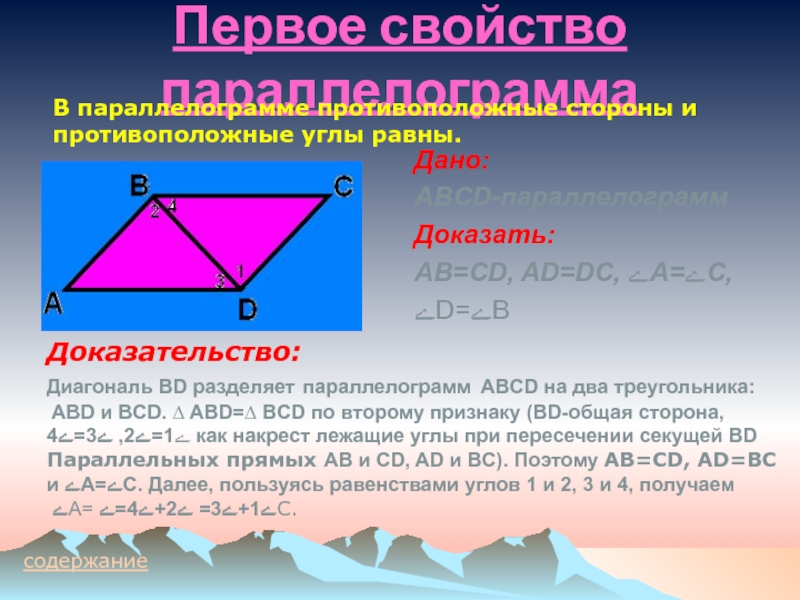
В параллелограмме противоположные стороны и
противоположные углы равны.
Доказательство:
Диагональ BD разделяет параллелограмм ABCD на два треугольника:
ABD и BCD. ∆ ABD=∆ BCD по второму признаку (BD-общая сторона,
ﮮ1=ﮮ2, ﮮ3=ﮮ4 как накрест лежащие углы при пересечении секущей BD
Параллельных прямых AB и CD, AD и BC). Поэтому AB=CD, AD=BC
и ﮮA=ﮮC. Далее, пользуясь равенствами углов 1 и 2, 3 и 4, получаем
ﮮА= ﮮ1+ﮮ3= ﮮ2+ﮮ4=ﮮС.
содержание
Слайд 5Второе свойство параллелограмма
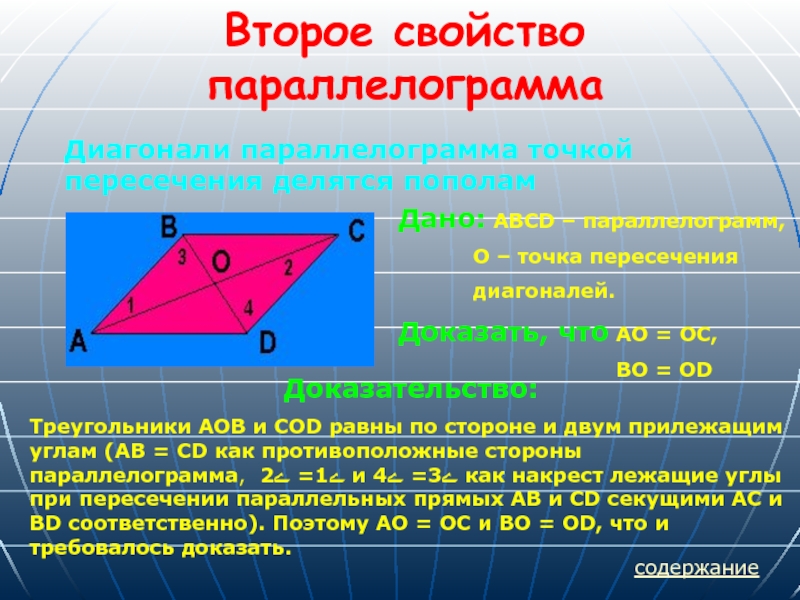
Диагонали параллелограмма точкой пересечения делятся пополам
Дано: ABCD – параллелограмм,
диагоналей.
Доказать, что АО = ОС,
ВО = ОD
Доказательство:
Треугольники AOB и COD равны по стороне и двум прилежащим углам (AB = CD как противоположные стороны параллелограмма, ﮮ1= ﮮ2 и ﮮ3= ﮮ4 как накрест лежащие углы при пересечении параллельных прямых AB и CD секущими AC и BD соответственно). Поэтому АО = ОС и ВО = ОD, что и требовалось доказать.
содержание
Слайд 6Задача
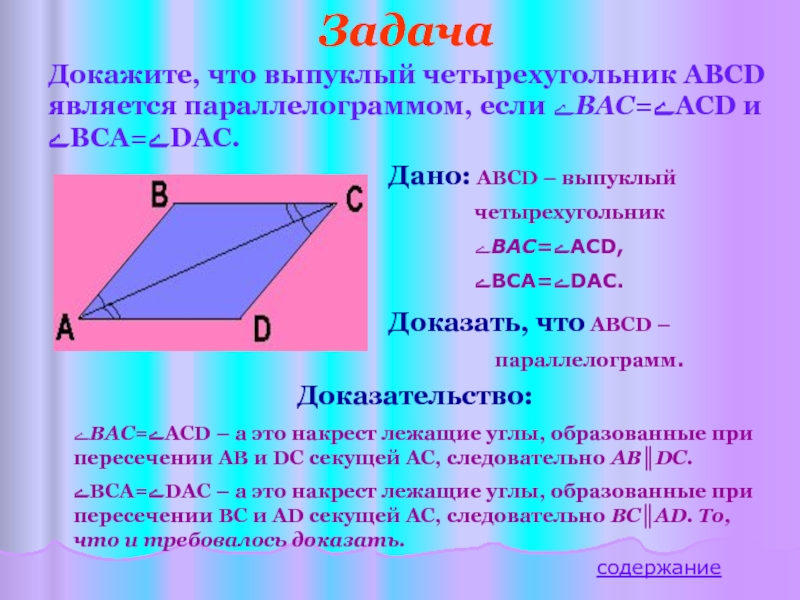
Докажите, что выпуклый четырехугольник ABCD является параллелограммом, если ﮮBAC=ﮮACD и ﮮBCA=ﮮDAC.
Дано: ABCD – выпуклый
четырехугольник
ﮮBAC=ﮮACD,
ﮮBCA=ﮮDAC.
Доказать, что ABCD –
параллелограмм.
Доказательство:
ﮮBAC=ﮮACD – а это накрест лежащие углы, образованные при пересечении AB и DC секущей AC, следовательно AB║DС.
ﮮBCA=ﮮDAC – а это накрест лежащие углы, образованные при пересечении BС и АD секущей AC, следовательно BС║АD. То, что и требовалось доказать.
содержание
Слайд 7Вопросы и задачи:
Дайте определение параллелограмма. Является ли параллелограмм выпуклым четырехугольником?
Докажите, что
Докажите, что диагонали параллелограмма точкой пересечения делятся пополам.
Докажите, что выпуклый четырехугольник ABCD является параллелограммом, если AB║CD, ﮮA=ﮮC.
Периметр параллелограмма равен 48 см. Найдите стороны параллелограмма, если одна сторона на 3 см больше другой.
Периметр параллелограмма ABCD равен 50 см, ﮮC=30ْ , а перпендикуляр BH к прямой CD равен 6,5 см. Найдите стороны параллелограмма.
В параллелограмме MNPQ проведен перпендикуляр NH к прямой MQ, причем точка H лежит на стороне MQ. Найдите стороны и углы параллелограмма, если известно, что MH = 3 см, HQ = 5 см, ﮮMNH = 30ْ.
содержание
Слайд 8Самостоятельная работа
Вариант 1
Периметр параллелограмма равен 48 см.Найдите стороны параллелограмма, если разность
Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К. Найдите периметр этого параллелограмма, если ВК = 15 см, КС = 9 см.
Вариант 2
Периметр параллелограмма равен 48 см. Найдите стороны параллелограмма, если одна из сторон в два раза больше другой.
Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.
содержание