- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Треугольники
Содержание
- 1. Презентация по геометрии на тему Треугольники
- 2. Треугольники АВС∆АВС( . ) А,В,С – вершины;АВ, ВС, АС – стороны;
- 3. Треугольники равны, если они при наложении совмещаются если
- 4. Признаки равенства треугольников СУСПо двум сторонам и углу между ними.Доказательство: (наложением)1.
- 5. 2. По стороне и двум прилежащим к ней углам.Доказательство: (наложением)3. По трем сторонам.Доказательство: (приложением)УСуССС
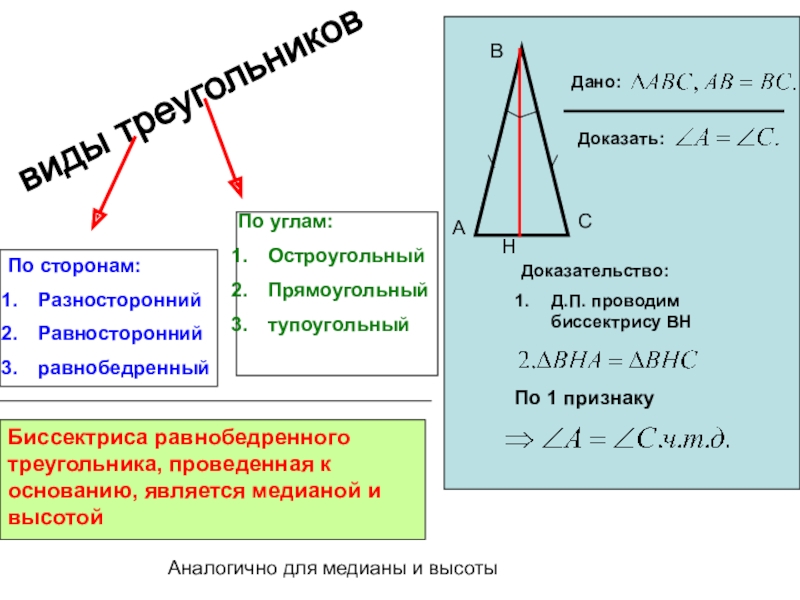
- 6. виды треугольников По сторонам:РазностороннийРавностороннийравнобедренныйПо углам:ОстроугольныйПрямоугольныйтупоугольныйДано:Доказать:Доказательство:Д.П. проводим биссектрису
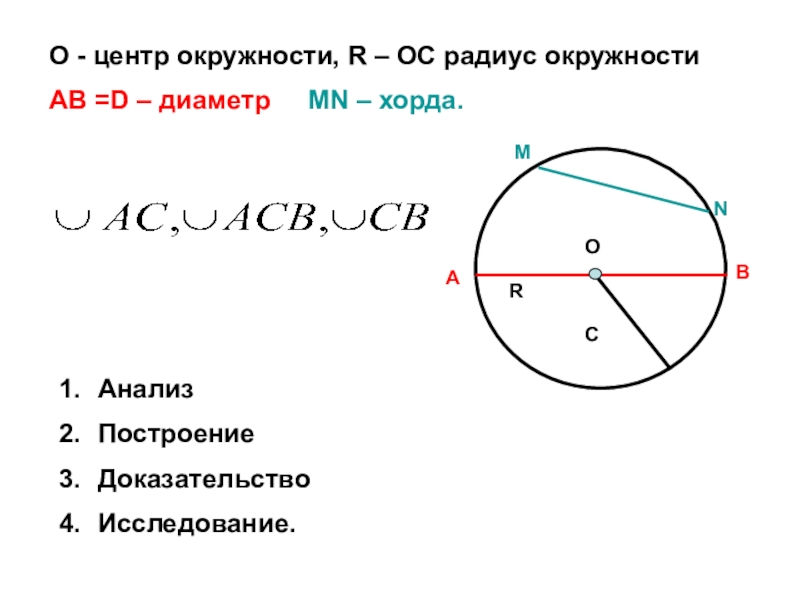
- 7. АнализПостроениеДоказательствоИсследование.ОАВСRMNО - центр окружности, R – ОС
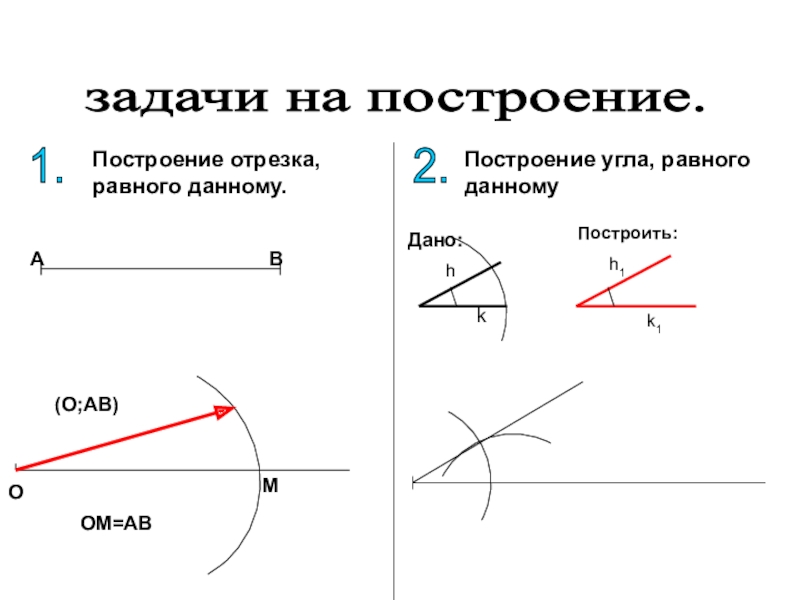
- 8. задачи на построение. 1. Построение отрезка, равного данному.АВОМ(О;АВ)ОМ=АВ2. Построение угла, равного данномуДано:hkПостроить:h1k1
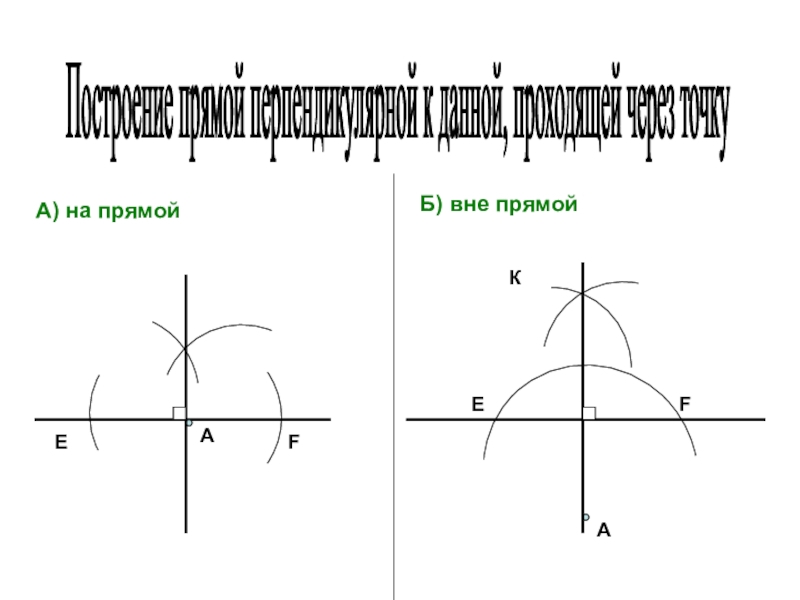
- 9. Построение прямой перпендикулярной к данной, проходящей через точку А) на прямойАБ) вне прямойАЕFКEF
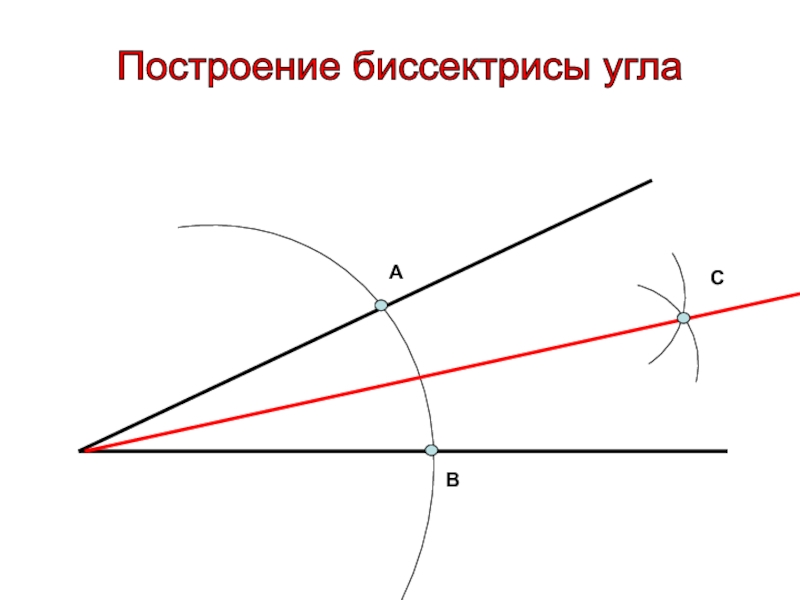
- 10. Построение биссектрисы угла АВС
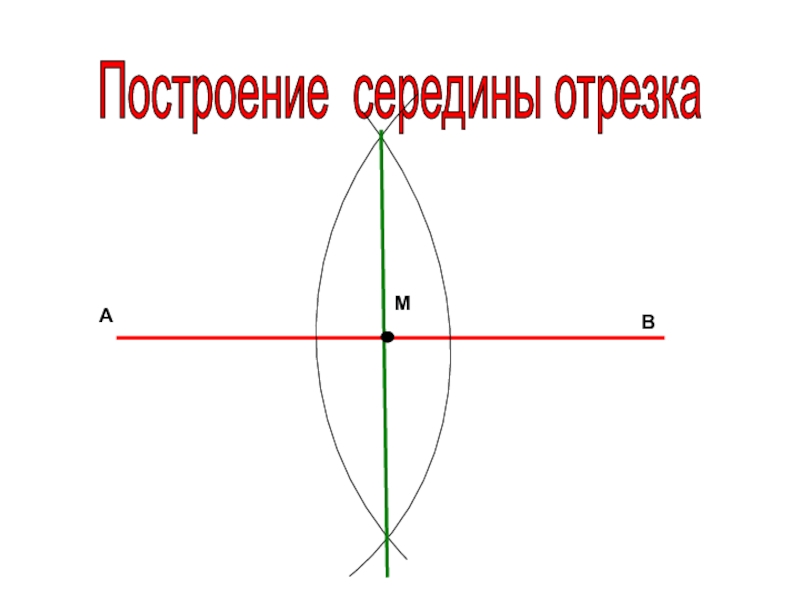
- 11. Построение середины отрезка АВМ
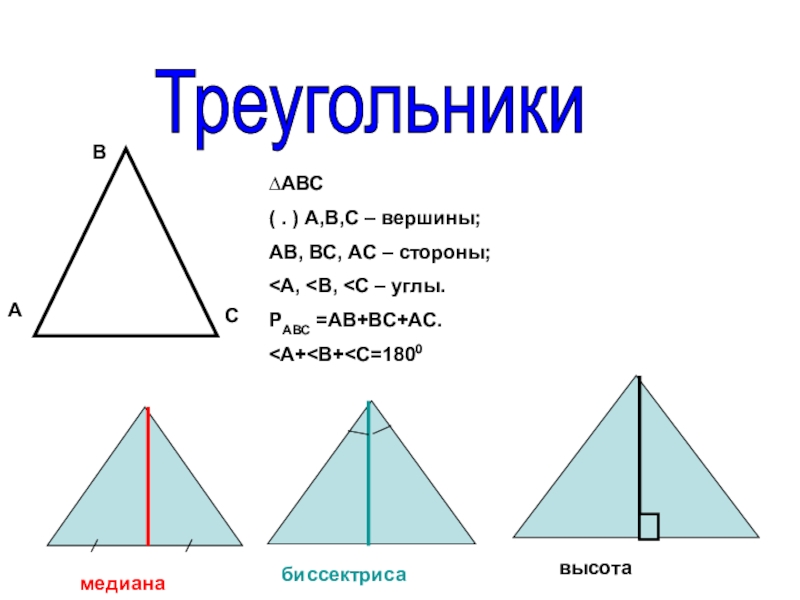
Треугольники АВС∆АВС( . ) А,В,С – вершины;АВ, ВС, АС – стороны;
Слайд 2Треугольники
А
В
С
∆АВС
( . ) А,В,С – вершины;
АВ, ВС, АС – стороны;
<В, <С – углы.
РАВС =АВ+ВС+АС.
<А+<В+<С=1800
РАВС =АВ+ВС+АС.
<А+<В+<С=1800
медиана
биссектриса
высота
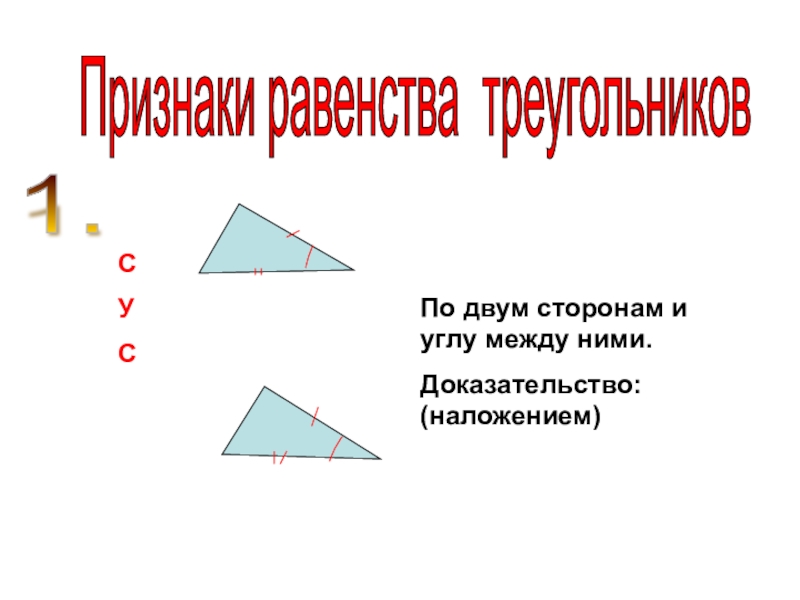
Слайд 4Признаки равенства треугольников
С
У
С
По двум сторонам и углу между ними.
Доказательство:
(наложением)
1.
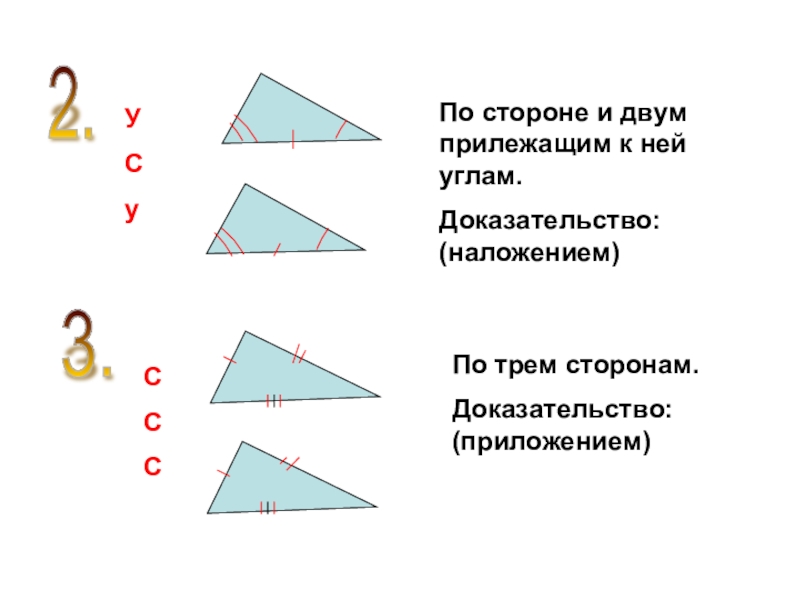
Слайд 52.
По стороне и двум прилежащим к ней углам.
Доказательство:
(наложением)
3.
По трем
сторонам.
Доказательство: (приложением)
Доказательство: (приложением)
У
С
у
С
С
С
Слайд 6
виды треугольников
По сторонам:
Разносторонний
Равносторонний
равнобедренный
По углам:
Остроугольный
Прямоугольный
тупоугольный
Дано:
Доказать:
Доказательство:
Д.П. проводим биссектрису ВН
По 1 признаку
А
В
С
Н
Биссектриса равнобедренного
треугольника, проведенная к основанию, является медианой и высотой
Аналогично для медианы и высоты
Слайд 7Анализ
Построение
Доказательство
Исследование.
О
А
В
С
R
M
N
О - центр окружности, R – ОС радиус окружности
АВ =D –
диаметр MN – хорда.
Слайд 8задачи на построение.
1.
Построение отрезка, равного данному.
А
В
О
М
(О;АВ)
ОМ=АВ
2.
Построение угла, равного
данному
Дано:
h
k
Построить:
h1
k1
Слайд 9Построение прямой перпендикулярной к данной, проходящей через точку
А) на прямой
А
Б)
вне прямой
А
Е
F
К
E
F