- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Сумма углов треугольника
Содержание
- 1. Презентация по геометрии на тему Сумма углов треугольника
- 2. 1445°47°
- 3. Древние греки на основе наблюдений и из
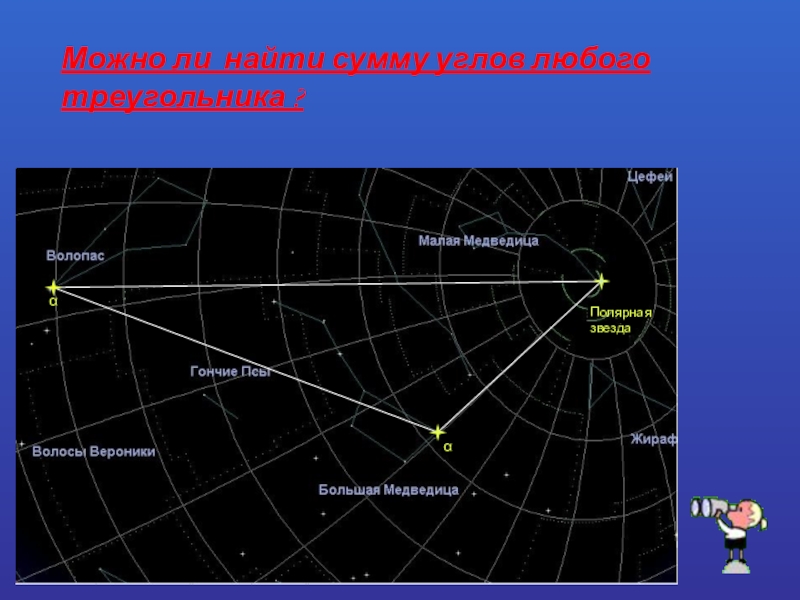
- 4. Полярная звездаα αМожно ли найти сумму углов любого треугольника ?
- 5. сумма углов треугольника Девиз урока: «В споре рождается истина».
- 6. ИЗ ИСТОРИИ МАТЕМАТИКИ ЕВКЛИД (ΙΙΙ в. до
- 7. ПОСИДОНИЙ (Ι в. до н. э.): Две
- 8. ТЕОРЕМА. СУММА УГЛОВ ТРЕУГОЛЬНИКА РАВНА 180°.АВС123ДАНО: ΔАВС.ДОКАЗАТЬ: ∠1
- 9. АВСЕD12345 Чертеж учеников Пифагора.Первое доказательство было сделано
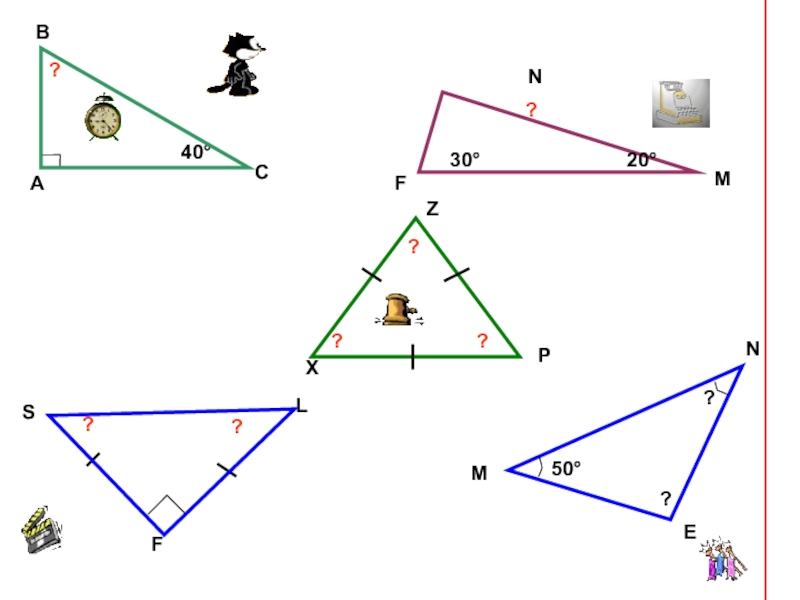
- 10. ?АВС40°?NFM?30°20°??? ??SLFXZP50°?NEМ
- 11. Решение.ΔABD- равнобедренный ∠А=∠D (св.
- 12. ЗАДАЧА. Найдите углы треугольника АВС, если ∠А
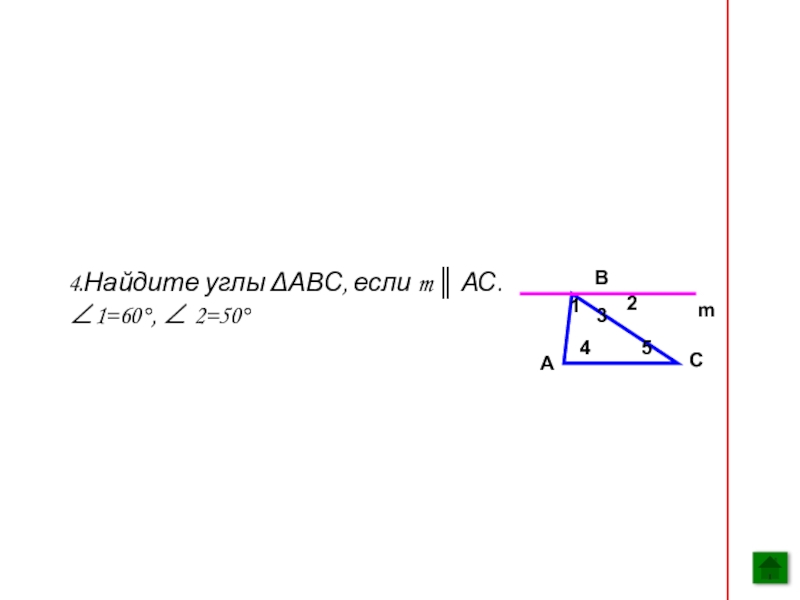
- 13. 4.Найдите углы ΔАВС, если m ║ АС.∠1=60°, ∠ 2=50°АСВm45 132
- 14. ДОМАШНЕЕ ЗАДАНИЕ п. 30 (теорема ),
Слайд 21
4
45°
47°
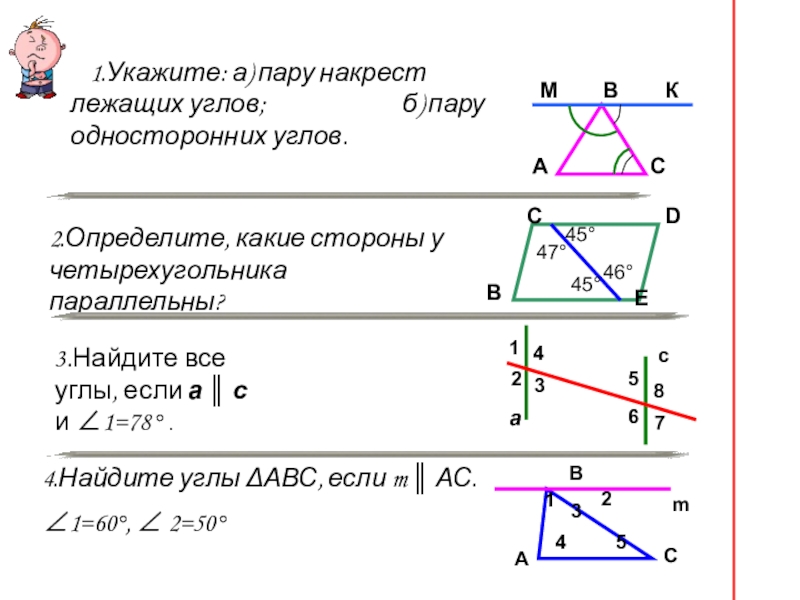
1.Укажите: а) пару
А
С
В
М
К
В
С
D
Е
2.Определите, какие стороны у четырехугольника параллельны?
45°
46°
3.Найдите все углы, если а ║ с и ∠1=78° .
а
2
3
8
7
5
6
4.Найдите углы ΔАВС, если m ║ АС.
∠1=60°, ∠ 2=50°
А
С
В
m
4
5
1
3
2
с
Слайд 3
Древние греки на основе наблюдений и из практического опыта делали выводы,
ПРАКТИЧЕСКАЯ РАБОТА
Опыт 1.
Постройте в тетради остроугольный, прямоугольный, тупоугольный треугольники, измерьте их углы и найдите их сумму в каждом треугольнике.
ОПЫТ 2.
Оторвите углы моделей треугольников и составьте из них угол.
Слайд 6
ИЗ ИСТОРИИ МАТЕМАТИКИ
ЕВКЛИД (ΙΙΙ в. до н. э.) До наших
Здесь же появляется теорема о сумме углов треугольника.
Слайд 7ПОСИДОНИЙ (Ι в. до н. э.): Две прямые, лежащие в одной
ИЗ ИСТОРИИ МАТЕМАТИКИ
Древнегреческий учёный ПАПП (вторая половина ΙΙΙ в. до н.э.) ввел символ параллельности прямых – знак = .
С 1557г. знак = используется как знак равенства (ввел Роберт Рекорд- английский врач и математик)
Знак параллельности прямых ║ ввел в 1677г. Уильям Оутред.
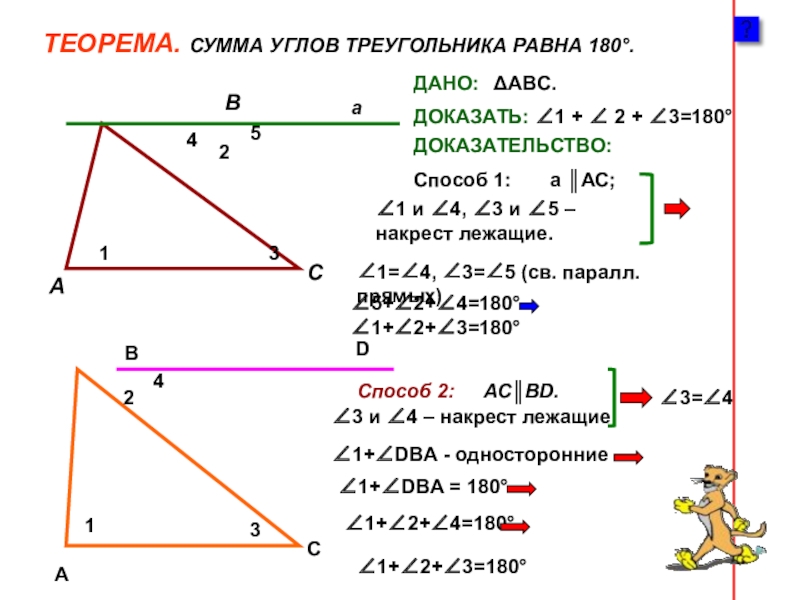
Слайд 8ТЕОРЕМА. СУММА УГЛОВ ТРЕУГОЛЬНИКА РАВНА 180°.
А
В
С
1
2
3
ДАНО: ΔАВС.
ДОКАЗАТЬ: ∠1 + ∠ 2 +
а
4
5
А
В
С
D
1
2
3
4
ДОКАЗАТЕЛЬСТВО:
Способ 1: а ║АС;
Способ 2: АС║ВD.
∠1 и ∠4, ∠3 и ∠5 – накрест лежащие.
∠1=∠4, ∠3=∠5 (св. паралл. прямых)
∠5+∠2+∠4=180° ∠1+∠2+∠3=180°
∠3 и ∠4 – накрест лежащие
∠3=∠4
∠1+∠DBA - односторонние
∠1+∠DBA = 180°
∠1+∠2+∠4=180°
∠1+∠2+∠3=180°
Слайд 9
А
В
С
Е
D
1
2
3
4
5
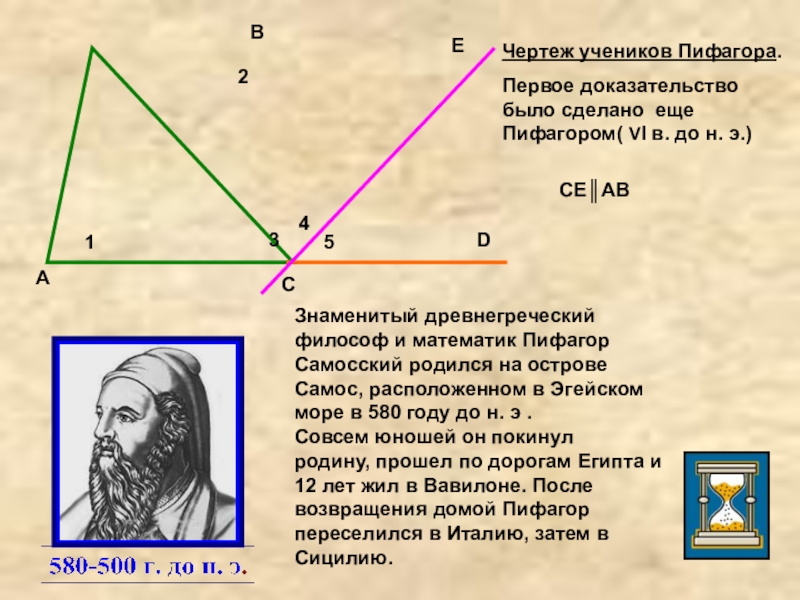
Чертеж учеников Пифагора.
Первое доказательство было сделано еще Пифагором( VΙ в.
Знаменитый древнегреческий философ и математик Пифагор Самосский родился на острове Самос, расположенном в Эгейском море в 580 году до н. э .
Совсем юношей он покинул
родину, прошел по дорогам Египта и 12 лет жил в Вавилоне. После возвращения домой Пифагор переселился в Италию, затем в Сицилию.
СЕ║АВ
Слайд 11
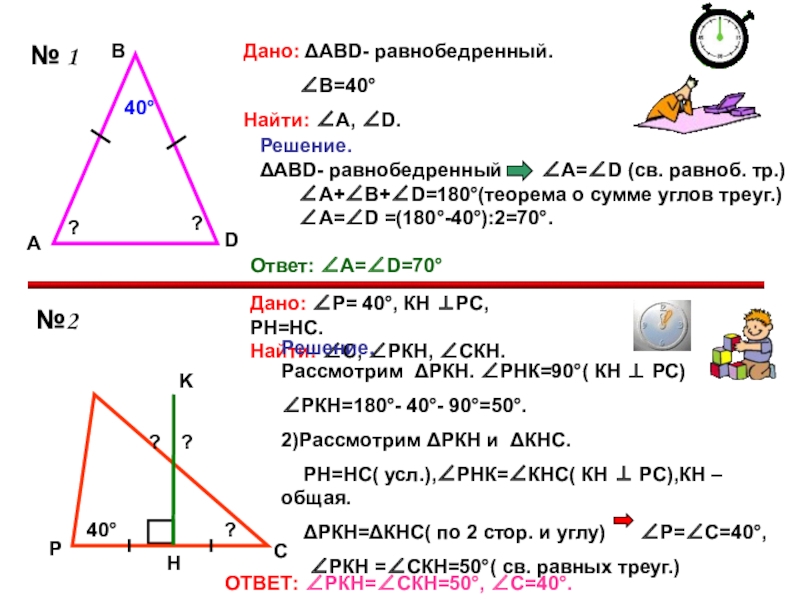
Решение.
ΔABD- равнобедренный ∠А=∠D (св. равноб. тр.)
∠А=∠D =(180°-40°):2=70°.
Дано: ΔABD- равнобедренный.
∠В=40°
Найти: ∠А, ∠D.
40°
?
?
А
В
D
?
40°
?
?
P
K
C
Н
Ответ: ∠А=∠D=70°
№ 1
№2
Дано: ∠Р= 40°, КН ⊥РС, РН=НС.
Найти: ∠С, ∠РКН, ∠СКН.
Решение. 1)Рассмотрим ΔРКН. ∠РНК=90°( КН ⊥ РС)
∠РКН=180°- 40°- 90°=50°.
2)Рассмотрим ΔРКН и ΔКНС.
РН=НС( усл.),∠РНК=∠КНС( КН ⊥ РС),КН – общая.
ΔРКН=ΔКНС( по 2 стор. и углу) ∠Р=∠С=40°,
∠РКН =∠СКН=50°( св. равных треуг.)
ОТВЕТ: ∠РКН=∠СКН=50°, ∠С=40°.
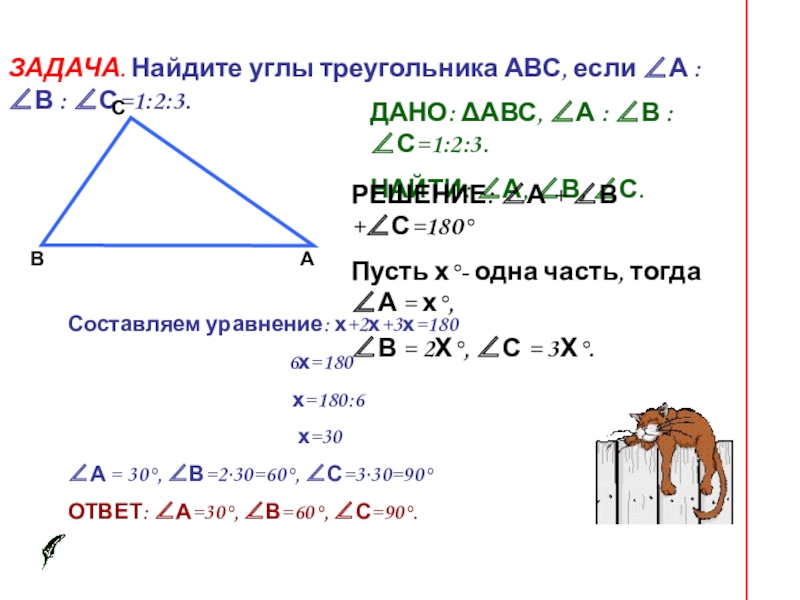
Слайд 12ЗАДАЧА. Найдите углы треугольника АВС, если ∠А : ∠В : ∠С=1:2:3.
В
С
А
ДАНО: ΔАВС, ∠А : ∠В : ∠С=1:2:3.
НАЙТИ: ∠А, ∠В, ∠С.
РЕШЕНИЕ: ∠А + ∠В +∠С=180°
Пусть х°- одна часть, тогда ∠А = х°,
∠В = 2Х°, ∠С = 3Х°.
Составляем уравнение: х+2х+3х=180
6х=180
х=180:6
х=30
∠А = 30°, ∠В=2·30=60°, ∠С=3·30=90°
ОТВЕТ: ∠А=30°, ∠В=60°, ∠С=90°.