10 Б 06.10.2015 год
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему: Скрещивающиеся прямые
Содержание
- 1. Презентация по геометрии на тему: Скрещивающиеся прямые
- 2. *Ребята! Сегодня мы с вами выходим в
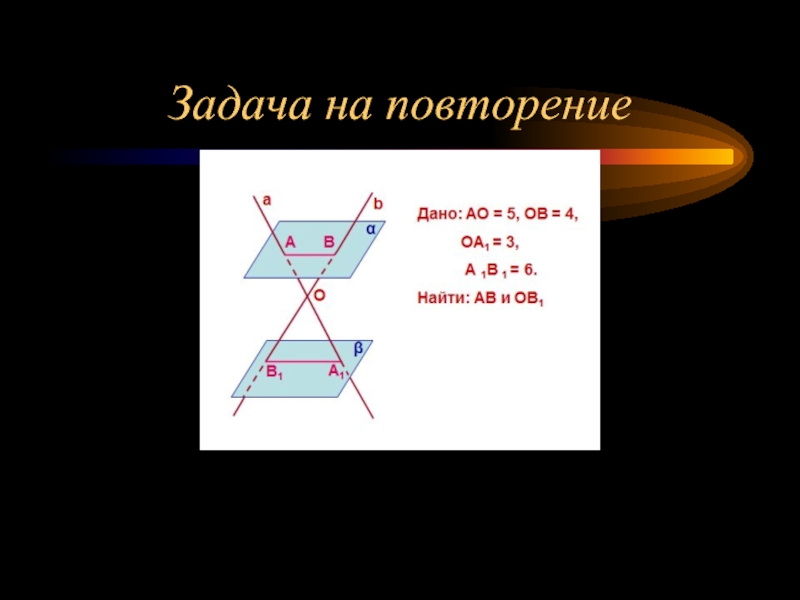
- 3. Задача на повторение
- 4. *Скрещивающиеся прямые лежат в параллельных плоскостях.ba1 свойствоВопрос
- 5. *Скрещивающиеся прямые лежат в параллельных плоскостях.ba1 свойствоВопрос №2: Как построить эти параллельные плоскости?a1b1
- 6. *Через точку, не лежащую на данных параллельных
- 7. *Через точку, не лежащую на данных параллельных
- 8. *У всяких двух скрещивающихся прямых имеется один общий перпендикуляр.abcAB3 свойствоВопрос №4: Как построить этот перпендикуляр?
- 9. *У всяких двух скрещивающихся прямых имеется один общий перпендикуляр.abcAB3 свойствоВопрос №4: Как построить этот перпендикуляр?a1
- 10. *Если одна из двух скрещивающихся прямых лежит
- 11. *Если одна из двух скрещивающихся прямых лежит
- 12. *Теперь вы догадываетесь, какие интересные конструкции можно
- 13. *Вы видите пары скрещивающихся ребер.
- 14. *А1В1 , АВ и D С –
- 15. *АС и В1D1– орбиты звездолетов, а точка
- 16. *Задание 3:B1Надо произвести запуск космического звездолета с
- 17. *А теперь попробуйте выполнить следующие задания.Задание 4:1.Докажите,
- 18. *Задание 5:АВСDА1В1С1D1 – космическая станция, имеющая форму
- 19. *О1О2Задание 2:Искомая прямая проходит через точку М
- 20. *Задание 3:C1АBCDD1A1В1МYXПостроениеПускО
- 21. *Задание 5:ОПостроениеЗамечаем, что прямая В1D лежит в
- 22. *Ответы:Т.к. прямые лежат в параллельных плоскостях, то
- 23. *Наше путешествие закончилось,но никогда не кончатся удивительныеоткрытия, которые вам предстоятпри дальнейшем изучении стереометрии.
*Ребята! Сегодня мы с вами выходим в открытое пространство. Объект изучения – скрещивающиеся прямые.Вы конечно помните, что две прямые называются скрещивающимися, если они не лежат в одной плоскости.Давайте посмотрим какими еще интересными свойствами обладают скрещивающиеся прямые.
Слайд 1*
Пересеченье двух миров
В какой произойдет момент?
А вдруг на стыке двух орбит
Нет
обозначенных планет?!
Слайд 2*
Ребята! Сегодня мы с вами выходим в открытое пространство. Объект изучения
– скрещивающиеся прямые.
Вы конечно помните, что две прямые называются скрещивающимися, если они не лежат в одной плоскости.
Давайте посмотрим какими еще интересными свойствами обладают скрещивающиеся прямые.
Слайд 4*
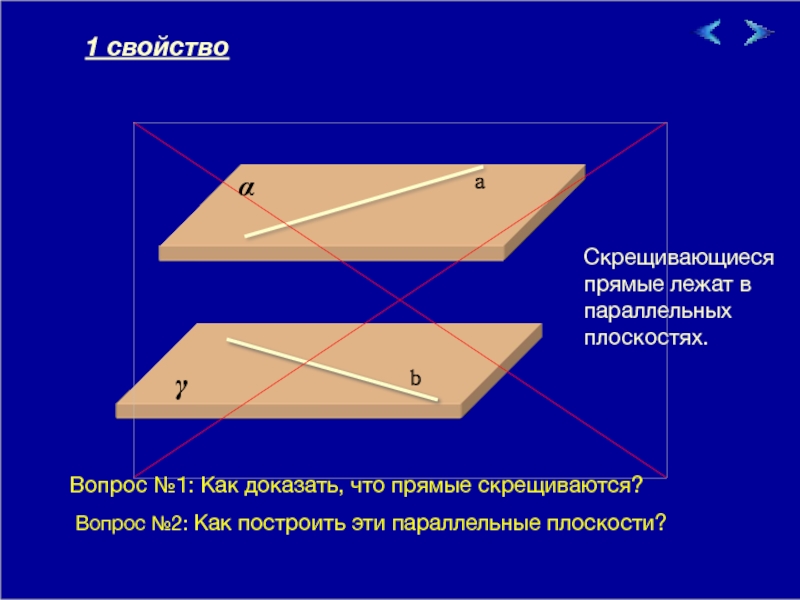
Скрещивающиеся прямые лежат в параллельных плоскостях.
b
a
1 свойство
Вопрос №1: Как доказать, что
прямые скрещиваются?
Вопрос №2: Как построить эти параллельные плоскости?
Вопрос №2: Как построить эти параллельные плоскости?
Слайд 5*
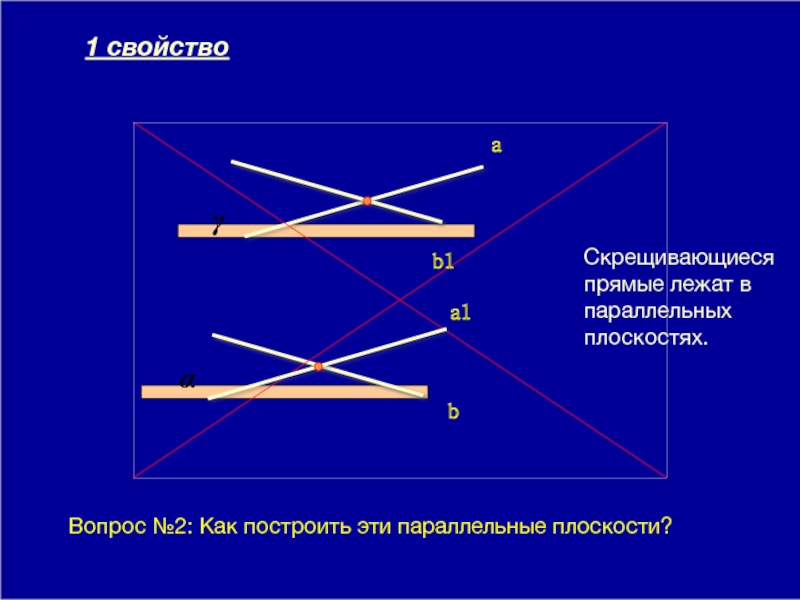
Скрещивающиеся прямые лежат в параллельных плоскостях.
b
a
1 свойство
Вопрос №2: Как построить эти
параллельные плоскости?
a1
b1
Слайд 6*
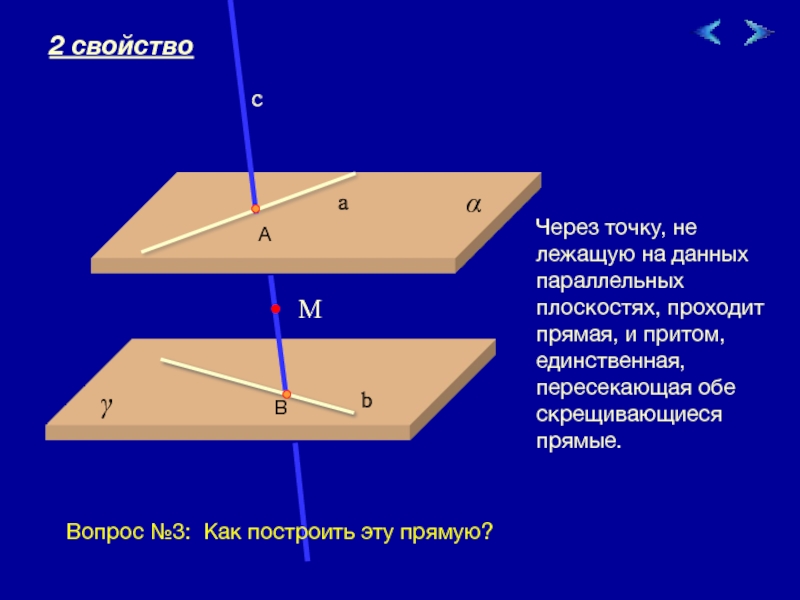
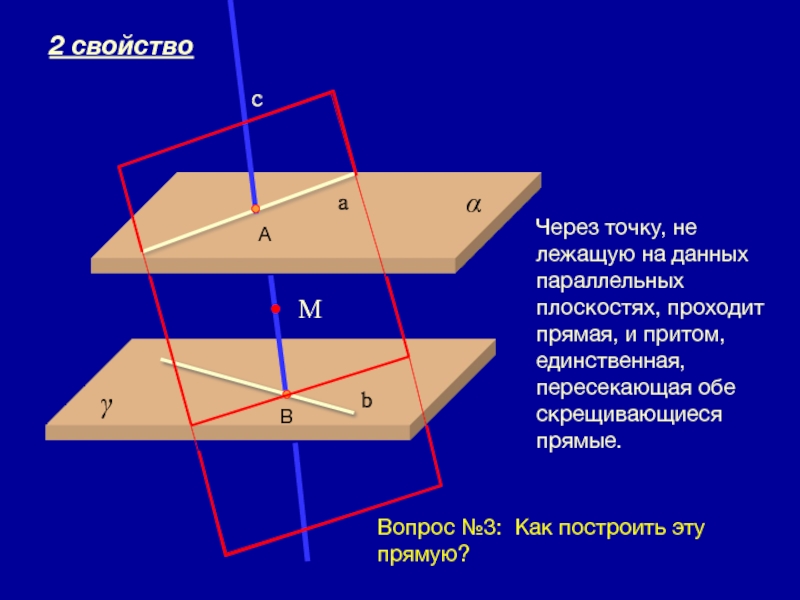
Через точку, не лежащую на данных параллельных плоскостях, проходит прямая, и
притом, единственная, пересекающая обе скрещивающиеся прямые.
М
a
b
c
A
B
2 свойство
Вопрос №3: Как построить эту прямую?
Слайд 7*
Через точку, не лежащую на данных параллельных плоскостях, проходит прямая, и
притом, единственная, пересекающая обе скрещивающиеся прямые.
М
a
b
c
A
B
2 свойство
Вопрос №3: Как построить эту прямую?
Слайд 8*
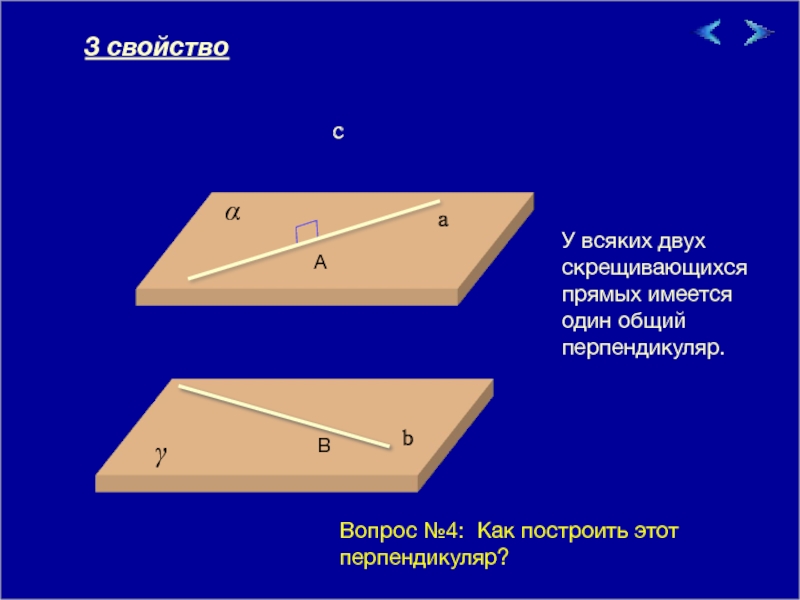
У всяких двух скрещивающихся прямых имеется один общий перпендикуляр.
a
b
c
A
B
3 свойство
Вопрос №4:
Как построить этот перпендикуляр?
Слайд 9*
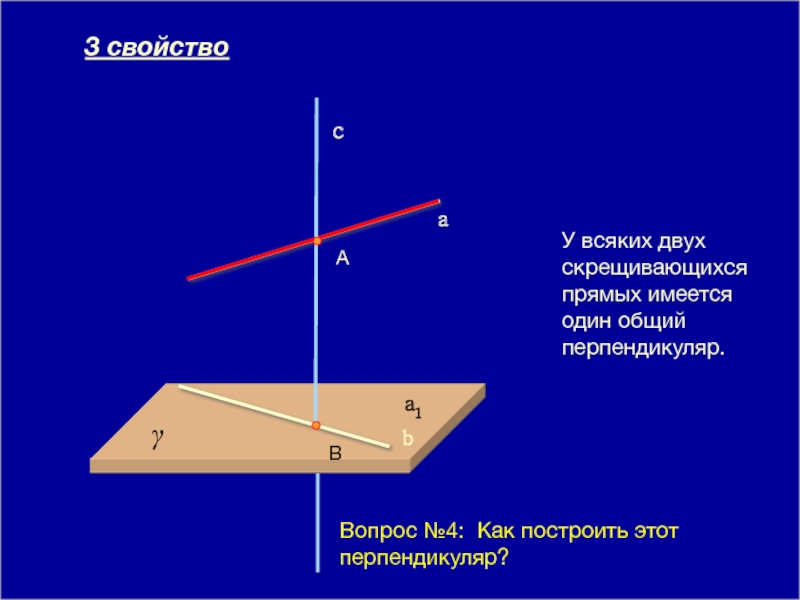
У всяких двух скрещивающихся прямых имеется один общий перпендикуляр.
a
b
c
A
B
3 свойство
Вопрос №4:
Как построить этот перпендикуляр?
a1
Слайд 10*
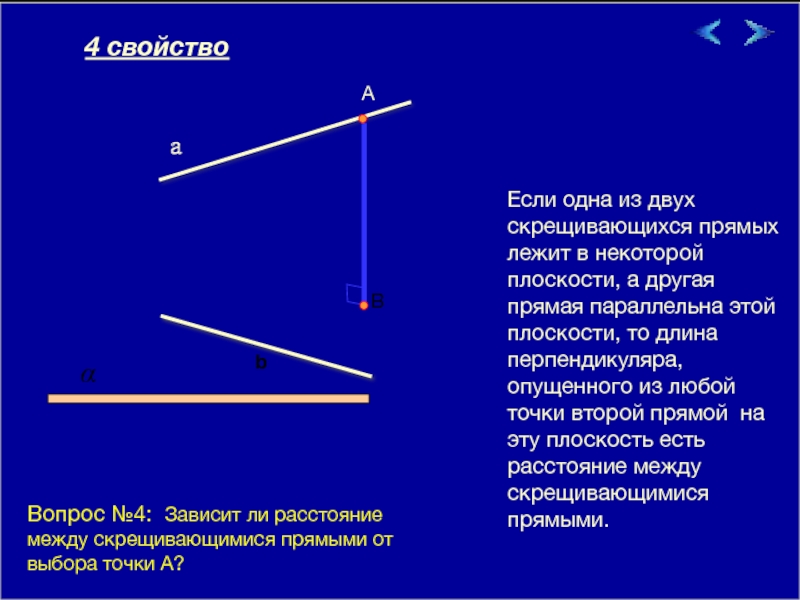
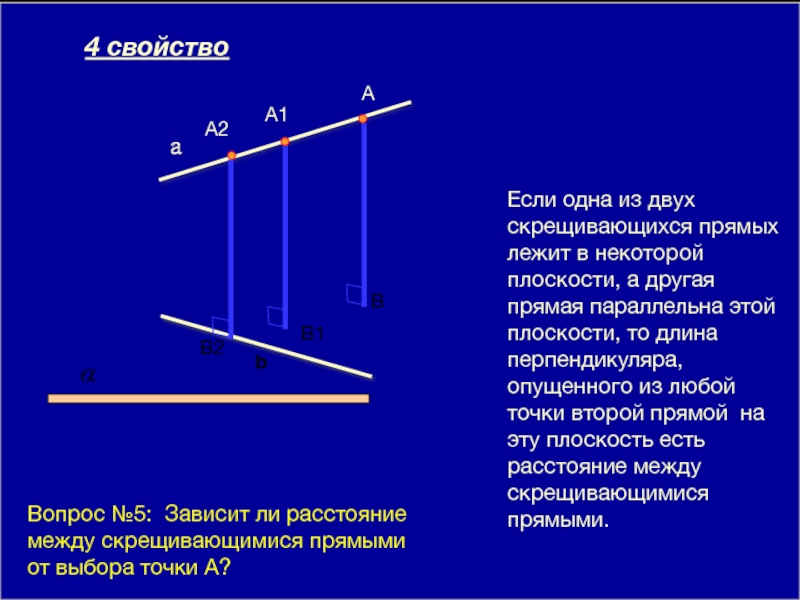
Если одна из двух скрещивающихся прямых лежит в некоторой плоскости, а
другая прямая параллельна этой плоскости, то длина перпендикуляра, опущенного из любой точки второй прямой на эту плоскость есть расстояние между скрещивающимися прямыми.
a
b
A
B
4 свойство
Вопрос №4: Зависит ли расстояние между скрещивающимися прямыми от выбора точки А?
Слайд 11*
Если одна из двух скрещивающихся прямых лежит в некоторой плоскости, а
другая прямая параллельна этой плоскости, то длина перпендикуляра, опущенного из любой точки второй прямой на эту плоскость есть расстояние между скрещивающимися прямыми.
a
b
A
B
4 свойство
Вопрос №5: Зависит ли расстояние между скрещивающимися прямыми от выбора точки А?
A1
A2
B1
B2
Слайд 12*
Теперь вы догадываетесь, какие интересные конструкции можно составлять из скрещивающихся прямых.
Без скрещивающихся ребер нет и многогранника.
Рассмотрим несколько моделей различных многогранников.
Слайд 14*
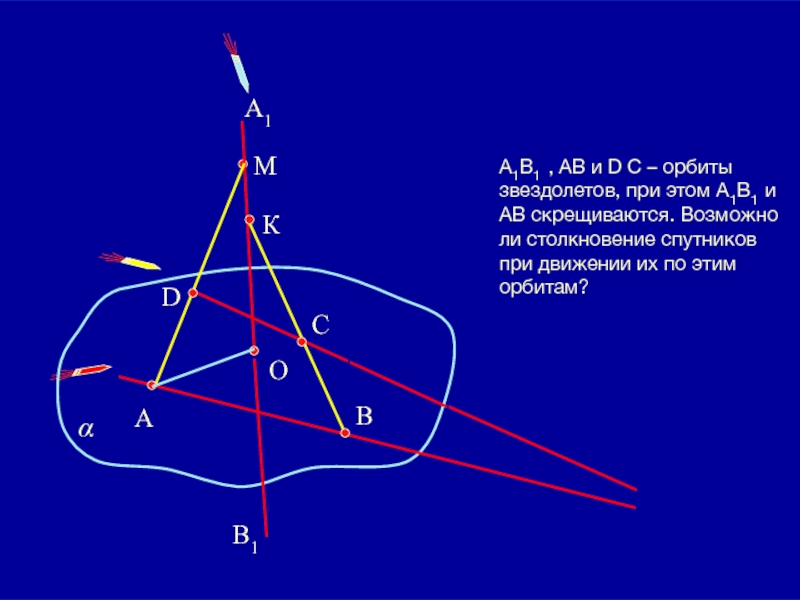
А1В1 , АВ и D С – орбиты звездолетов, при этом
А1В1 и АВ скрещиваются. Возможно ли столкновение спутников при движении их по этим орбитам?
Задание 1:
B1
B
C
D
A1
М
А
К
О
Слайд 15*
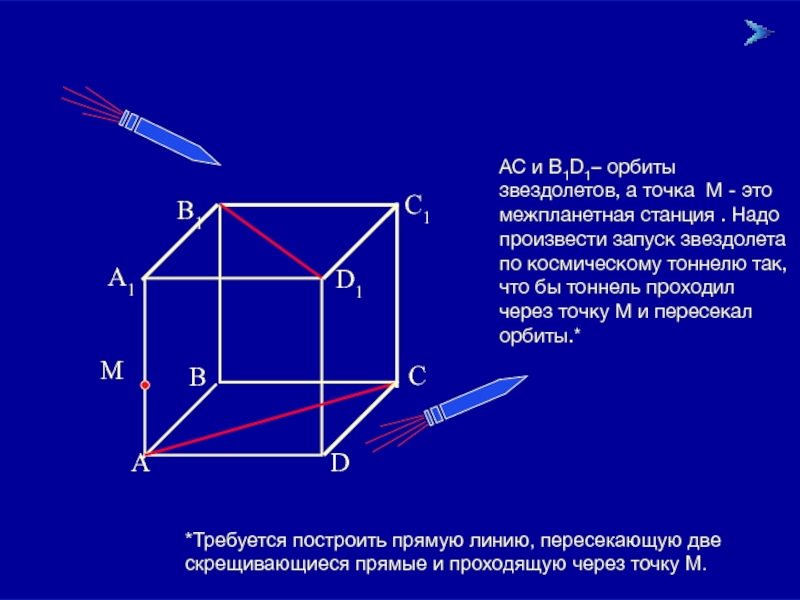
АС и В1D1– орбиты звездолетов, а точка М - это межпланетная
станция . Надо произвести запуск звездолета по космическому тоннелю так, что бы тоннель проходил через точку М и пересекал орбиты.*
Задание 2:
*Требуется построить прямую линию, пересекающую две скрещивающиеся прямые и проходящую через точку М.
А
Слайд 16*
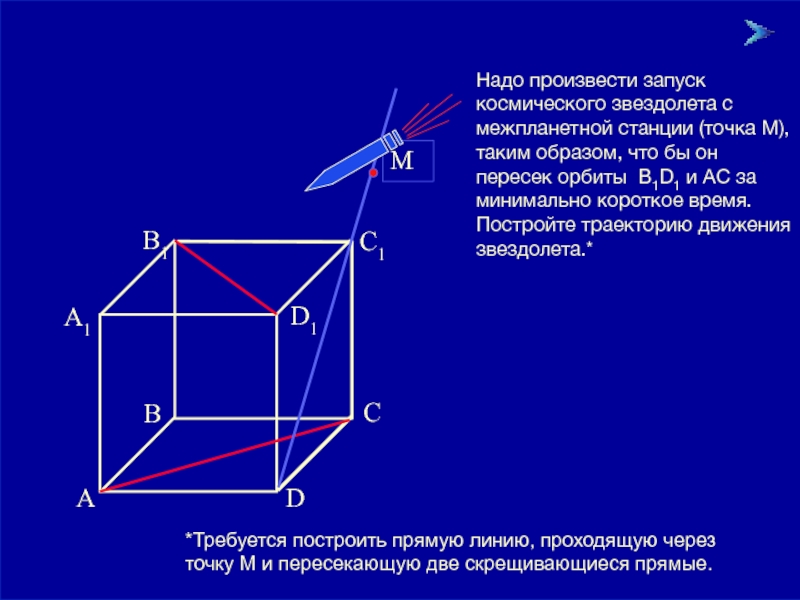
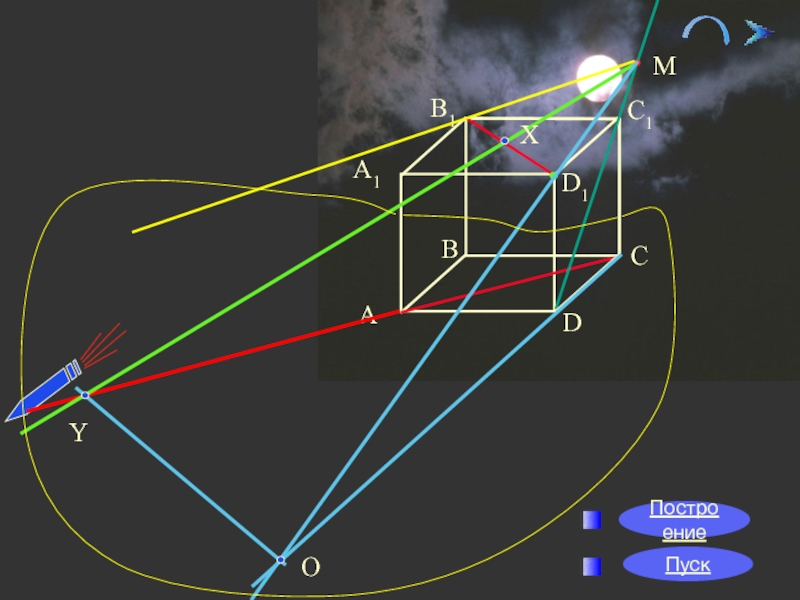
Задание 3:
B1
Надо произвести запуск космического звездолета с межпланетной станции (точка М),
таким образом, что бы он пересек орбиты В1D1 и АС за минимально короткое время. Постройте траекторию движения звездолета.*
*Требуется построить прямую линию, проходящую через точку М и пересекающую две скрещивающиеся прямые.
Слайд 17*
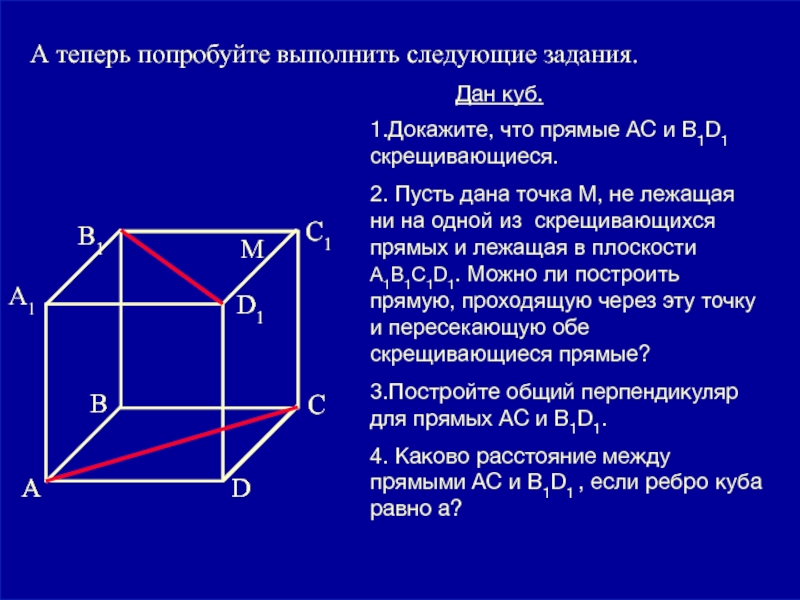
А теперь попробуйте выполнить следующие задания.
Задание 4:
1.Докажите, что прямые АС и
B1D1 скрещивающиеся.
2. Пусть дана точка М, не лежащая ни на одной из скрещивающихся прямых и лежащая в плоскости А1В1С1D1. Можно ли построить прямую, проходящую через эту точку и пересекающую обе скрещивающиеся прямые?
3.Постройте общий перпендикуляр для прямых АС и B1D1.
4. Каково расстояние между прямыми АС и В1D1 , если ребро куба равно а?
2. Пусть дана точка М, не лежащая ни на одной из скрещивающихся прямых и лежащая в плоскости А1В1С1D1. Можно ли построить прямую, проходящую через эту точку и пересекающую обе скрещивающиеся прямые?
3.Постройте общий перпендикуляр для прямых АС и B1D1.
4. Каково расстояние между прямыми АС и В1D1 , если ребро куба равно а?
А1
М
Дан куб.
Слайд 18*
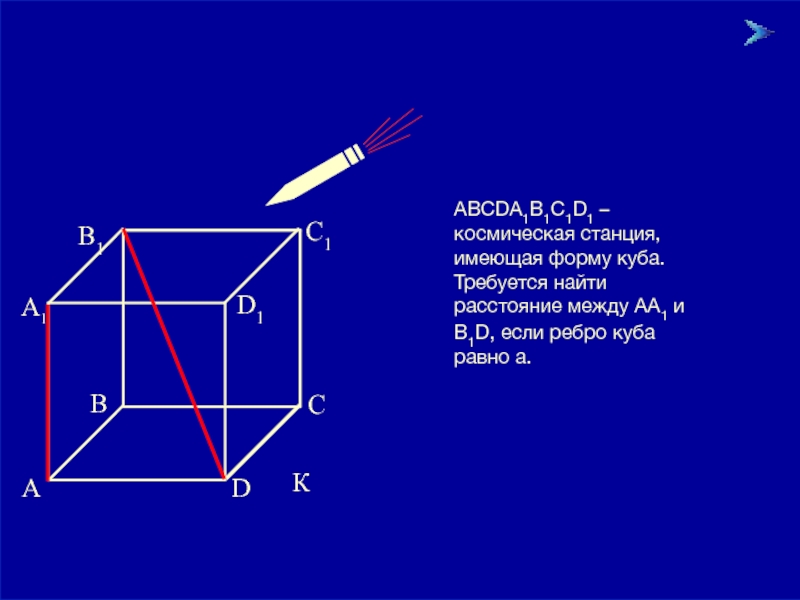
Задание 5:
АВСDА1В1С1D1 – космическая станция, имеющая форму куба. Требуется найти расстояние
между АА1 и В1D, если ребро куба равно а.
К
B1
C1
А
B
C
D
D1
А1
Слайд 19*
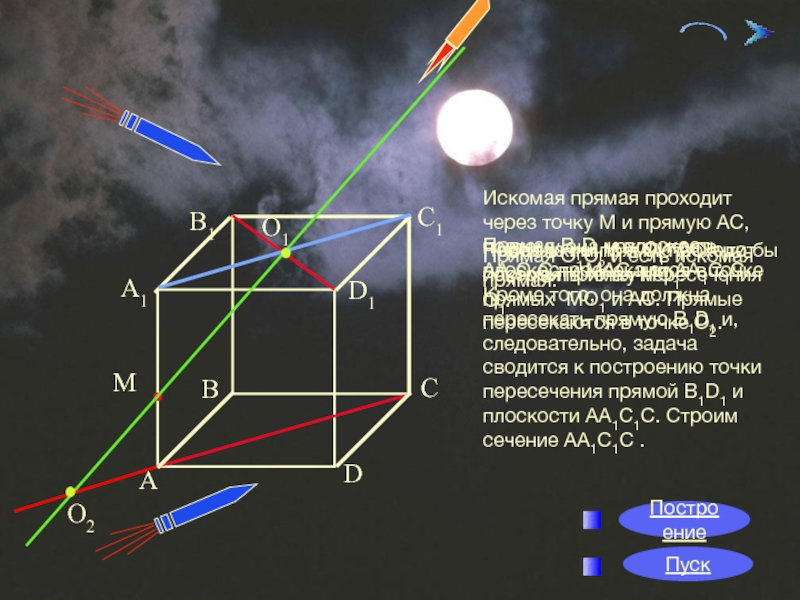
О1
О2
Задание 2:
Искомая прямая проходит через точку М и прямую АС, поэтому
она находится в плоскости МАС или АА1С1С. Кроме того, она должна пересекать прямую В1D1 и, следовательно, задача сводится к построению точки пересечения прямой В1D1 и плоскости АА1С1С. Строим сечение АА1С1С .
Прямая В1D1 и плоскость АА1С1С пересекаются в точке О1.
А
Через точки М и О1 проходит искомая прямая МО1.
Продолжим прямую АС, что бы построить точку пересечения прямых МО1 и АС. Прямые пересекаются в точке О2.
Прямая О1О2 и есть искомая прямая.
Построение
Пуск
Слайд 21*
Задание 5:
О
Построение
Замечаем, что прямая В1D лежит в плоскости сечения ВВ1D1D, а
прямая АА1 параллельна этой плоскости. Следовательно, что бы найти расстояние между прямыми АА1 и В1D надо опустить перпендикуляр из любой точки прямой АА1 на плоскость ВВ1D и найти его длину.
Опустим перпендикуляр АС на плоскость ВВ1D (объясни как).
АО и есть искомое расстояние.
Слайд 22*
Ответы:
Т.к. прямые лежат в параллельных плоскостях, то они не пересекаются, а
т.к. они не параллельны. Следовательно они скрещиваются.
Надо на одной из скрещивающихся прямых отметить произвольную точку и построить через эту точку прямую, параллельную второй скрещивающейся прямой. Затем через две пересекающиеся прямые построить 1-ю плоскость. Аналогичным образом поступить со второй плоскостью. (признак параллельности двух плоскостей).
Надо через одну из скрещивающихся прямых и данную точку построить плоскость. Вторая из скрещивающихся прямых будет пересекать эту плоскость в некоторой точке. Через эту точку и данную точку провести искомую прямую.
Надо через одну из скрещивающихся прямых провести плоскость, параллельную второй прямой и затем параллельным переносом опустить вторую прямую на эту плоскость, что бы найти точку пересечения прямых. Из этой точки восстановить перпендикуляр на вторую прямую.
Нет.
Надо на одной из скрещивающихся прямых отметить произвольную точку и построить через эту точку прямую, параллельную второй скрещивающейся прямой. Затем через две пересекающиеся прямые построить 1-ю плоскость. Аналогичным образом поступить со второй плоскостью. (признак параллельности двух плоскостей).
Надо через одну из скрещивающихся прямых и данную точку построить плоскость. Вторая из скрещивающихся прямых будет пересекать эту плоскость в некоторой точке. Через эту точку и данную точку провести искомую прямую.
Надо через одну из скрещивающихся прямых провести плоскость, параллельную второй прямой и затем параллельным переносом опустить вторую прямую на эту плоскость, что бы найти точку пересечения прямых. Из этой точки восстановить перпендикуляр на вторую прямую.
Нет.
Слайд 23*
Наше путешествие закончилось,
но никогда не кончатся удивительные
открытия, которые вам предстоят
при дальнейшем
изучении
стереометрии.
