- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Симметрия
Содержание
- 1. Презентация по геометрии на тему Симметрия
- 2. Симметрия относительно точкиАОТочки А и А1 называются
- 3. Две фигуры F и F1 называются симметричными
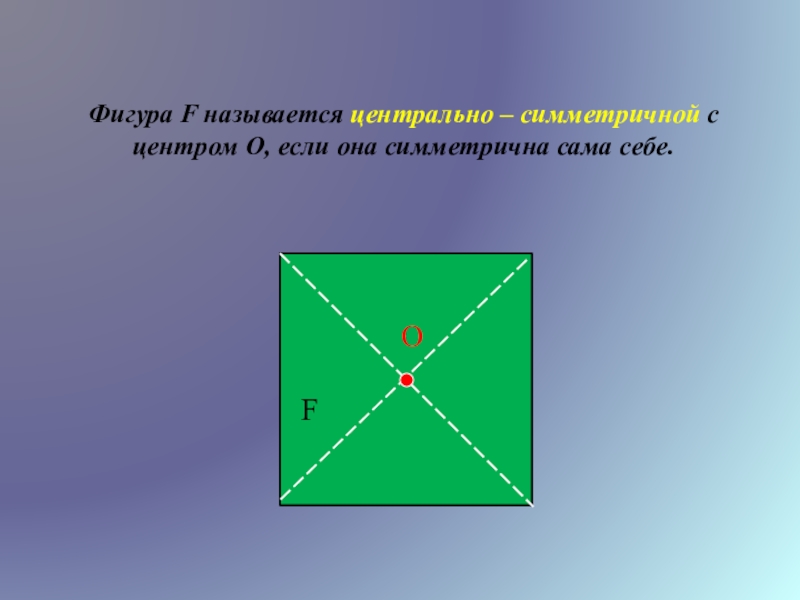
- 4. Фигура F называется центрально – симметричной с центром О, если она симметрична сама себе.FО
- 5. А1АОПостроить отрезок А1В1 симметричный отрезку АВ относительно
- 6. ОАВВ1СС1А1Построить треугольник А1В1С1 симметричный треугольнику АВС относительно
- 7. Слайд 7
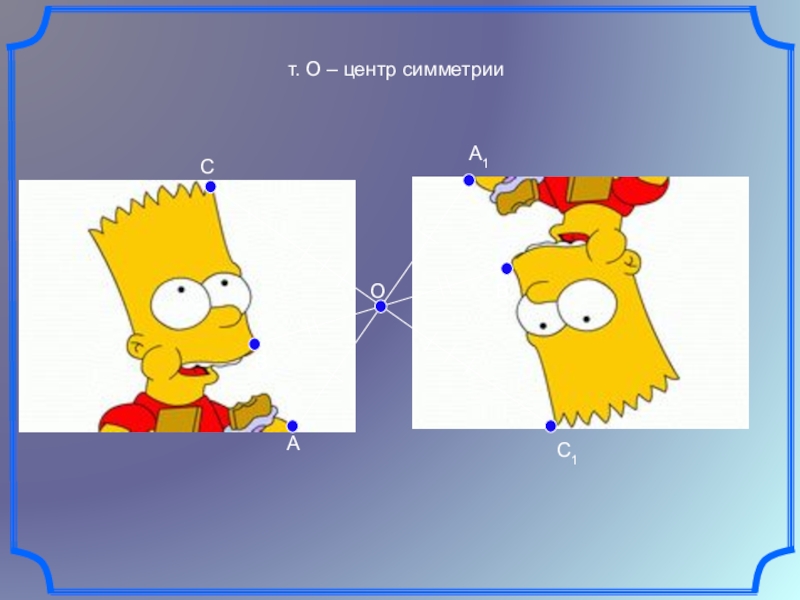
- 8. OAC1A1BB1Cт. О – центр симметрии
- 9. Симметрия относительно прямойДве точки А и А'
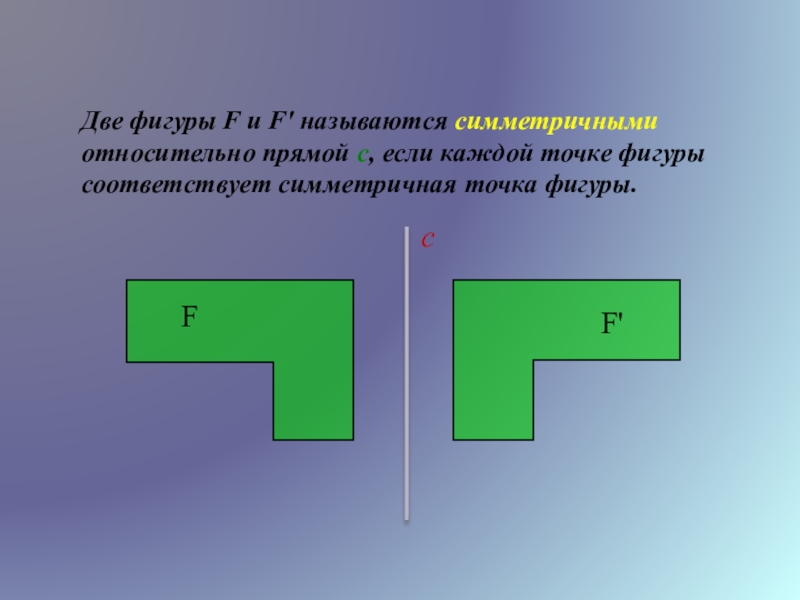
- 10. Две фигуры F и F' называются симметричными
- 11. Фигура F называется симметричной относительно прямой с, если она симметрична сама себе.с
- 12. Представление об осевой симметрии даёт, например, перегибание
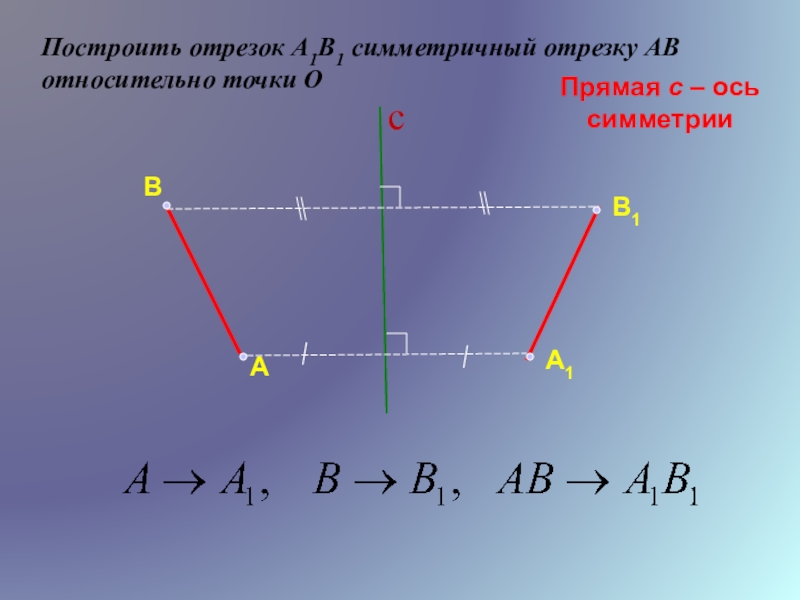
- 13. Построить отрезок А1В1 симметричный отрезку АВ относительно точки ОПрямая с – ось симметрииА1АВВ1c
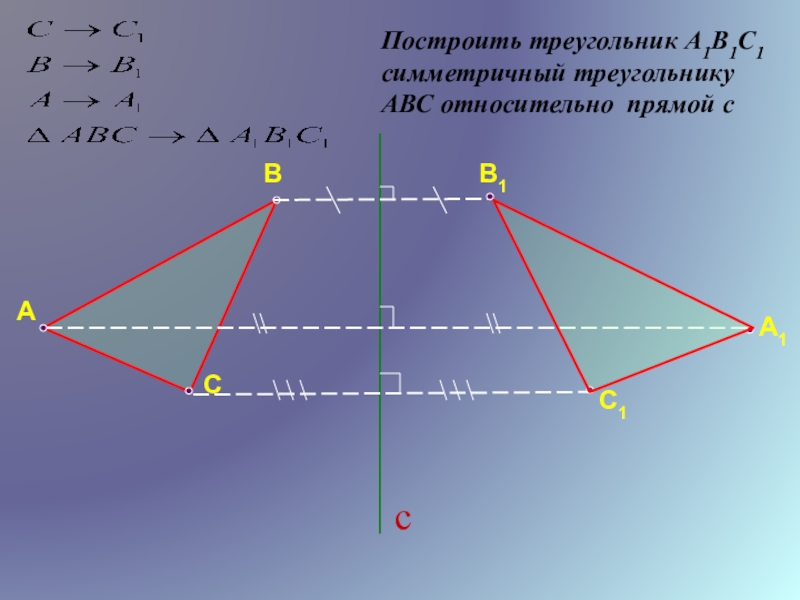
- 14. Построить треугольник А1В1С1 симметричный треугольнику АВС относительно прямой сАСВВ1А1С1c
- 15. http://www.point.ru/photo/galleries/12876/
- 16. http://www.point.ru/photo/galleries/12876/
- 17. Литература:Смирнов В.А., Смирнова И.М., Ященко И.В. Наглядная геометрия, 5-6 класс.
Симметрия относительно точкиАОТочки А и А1 называются симметричными относительно точки О (центр симметрии), если О – середина отрезка АА1.Точка О считается симметричной самой себе.Точка О – центр симметрииСимметрия относительно точки называется центральной симметриейА1
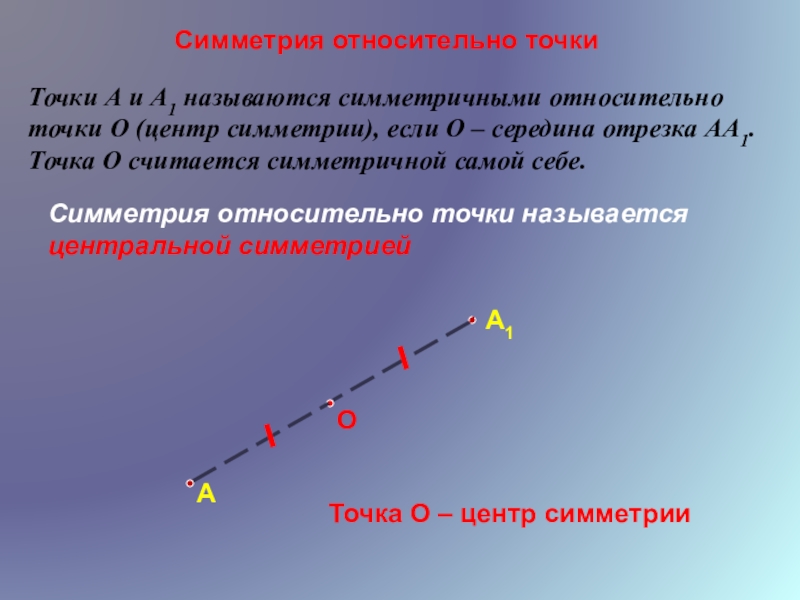
Слайд 2Симметрия относительно точки
А
О
Точки А и А1 называются симметричными относительно точки О
(центр симметрии), если О – середина отрезка АА1.
Точка О считается симметричной самой себе.
Точка О считается симметричной самой себе.
Точка О – центр симметрии
Симметрия относительно точки называется центральной симметрией
А1
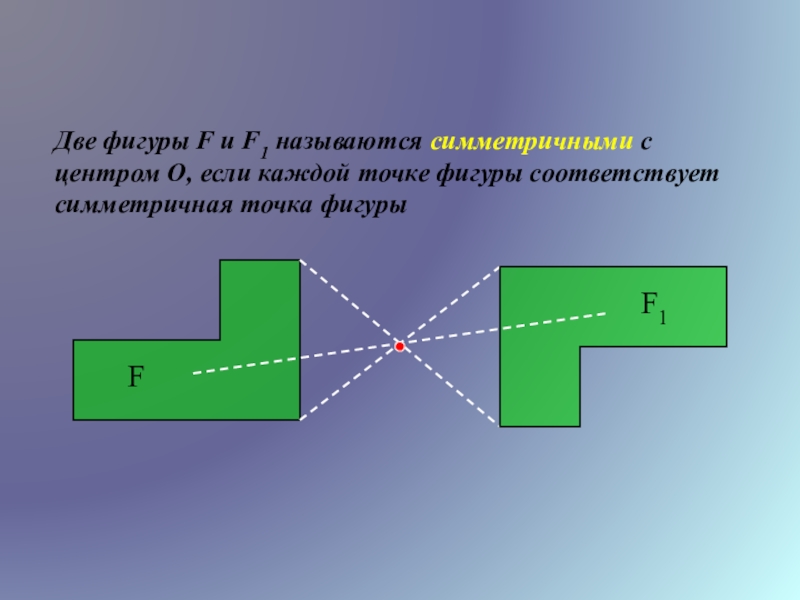
Слайд 3Две фигуры F и F1 называются симметричными с центром О, если
каждой точке фигуры соответствует симметричная точка фигуры
F
F1
Слайд 5А1
А
О
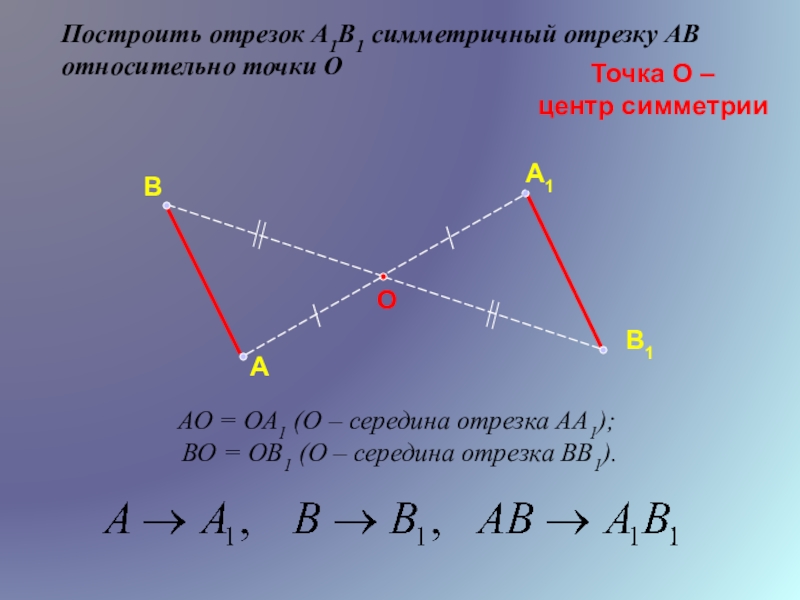
Построить отрезок А1В1 симметричный отрезку АВ относительно точки О
Точка О –
центр симметрии
В
В1
АО = ОА1 (О – середина отрезка АА1);
ВО = ОВ1 (О – середина отрезка ВВ1).
Слайд 6О
А
В
В1
С
С1
А1
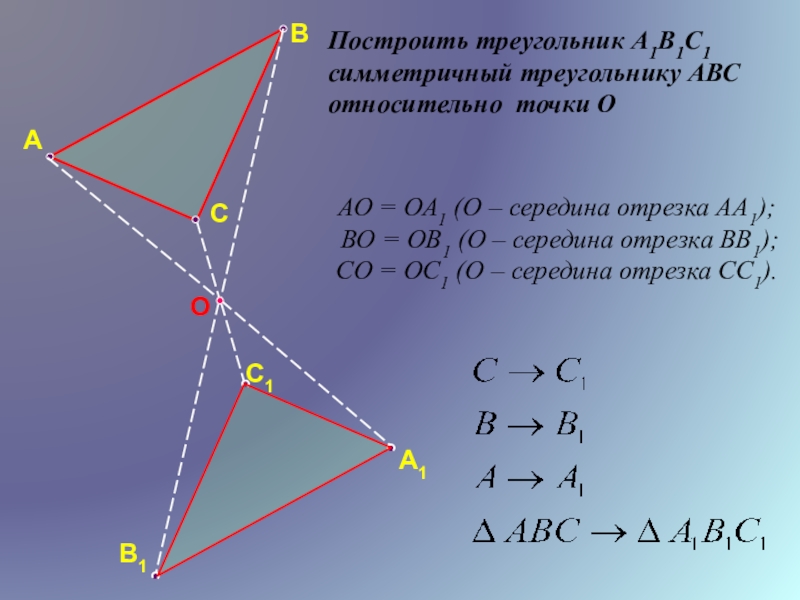
Построить треугольник А1В1С1 симметричный треугольнику АВС относительно точки О
АО = ОА1
(О – середина отрезка АА1);
ВО = ОВ1 (О – середина отрезка ВВ1);
СО = ОС1 (О – середина отрезка СС1).
ВО = ОВ1 (О – середина отрезка ВВ1);
СО = ОС1 (О – середина отрезка СС1).
Слайд 9Симметрия относительно прямой
Две точки А и А' называются симметричными относительно прямой
с, если эта прямая проходит через середину отрезка АА’ и перпендикулярна к нему (пересекаются под прямым углом). Каждая точка прямой с считается симметричной самой себе.
Прямая с называется осью симметрии.
А1
А
с
Слайд 10Две фигуры F и F' называются симметричными относительно прямой с, если
каждой точке фигуры соответствует симметричная точка фигуры.
F
F'
с
Слайд 12Представление об осевой симметрии даёт, например, перегибание и складывание листа бумаги.
Если перегнуть и сложить лист бумаги, то линию сгиба с можно считать изображающей часть прямой . Если при этом точка А на листе бумаги совмещается с точкой А’, то эти точки будут симметричными относительно линии сгиба с.
А
А'
с
Слайд 13Построить отрезок А1В1 симметричный отрезку АВ относительно точки О
Прямая с –
ось симметрии
А1
А
В
В1
c
