учитель математики
Артамонова Елена Львовна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему :Решение треугольников
Содержание
- 1. Презентация по геометрии на тему :Решение треугольников
- 2. Цели и задачи урока:Обобщить
- 3. Ход урокаОргмоментУстная разминкаЗакрепление изученного материалаПромежуточный контроль (тест)Домашнее задание
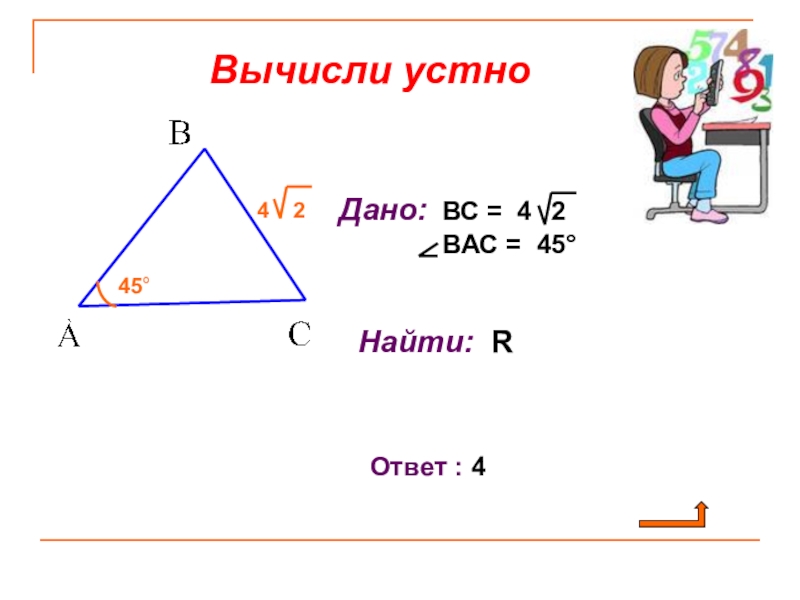
- 4. Устная разминка (теорема синусов и косинусов) Проверь себя !
- 5. Продолжи предложение: Решение треугольников -
- 6. Слайд 6
- 7. Слайд 7
- 8. Квадрат любой стороны треугольника равен сумме квадратов
- 9. Соединить линиями части фраз, соответствующие друг другу
- 10. Заполнить пропуски в равенствах. Дан
- 11. Дан
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Решение треугольниковЗадача № 1. Дано: a =
- 16. Решение треугольников
- 17. Слайд 17
- 18. Подготовка к экзаменамПлощадь параллелограмма равна 16√3,
- 19. Слайд 19
- 20. ТестГерберт Спенсер, английский философ, говорил: «Дороги
- 21. Слайд 21
- 22. Слайд 22
- 23. Спасибо за урок
Слайд 1Решение треугольников
Урок по геометрии
в 9 классе
Слайд 2 Цели и задачи урока:
Обобщить и закрепить знания теорем
Отработать нахождение неизвестных элементов в треугольнике
Развивать навыки самостоятельной работы и самооценки
Воспитывать интерес к математике
Слайд 3 Ход урока
Оргмомент
Устная разминка
Закрепление изученного материала
Промежуточный контроль (тест)
Домашнее
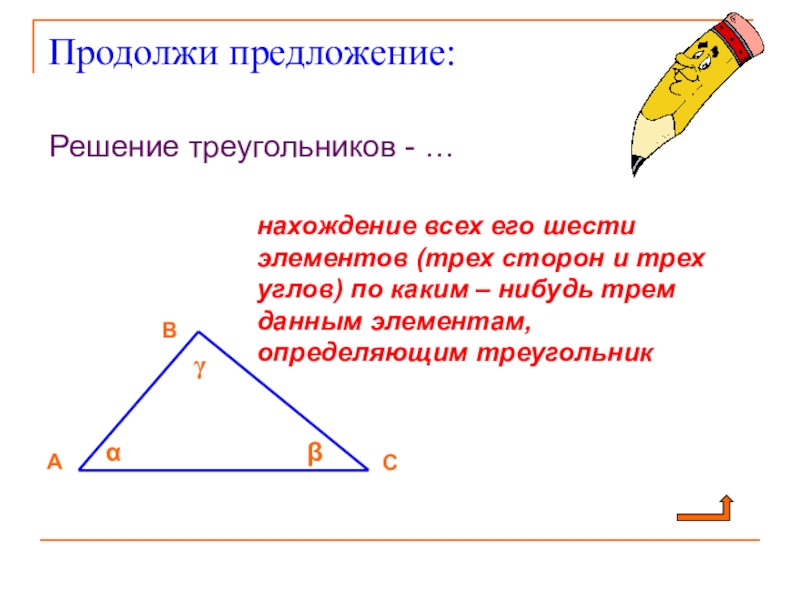
Слайд 5Продолжи предложение:
Решение треугольников - …
нахождение всех его шести элементов
А
В
С
α
γ
β
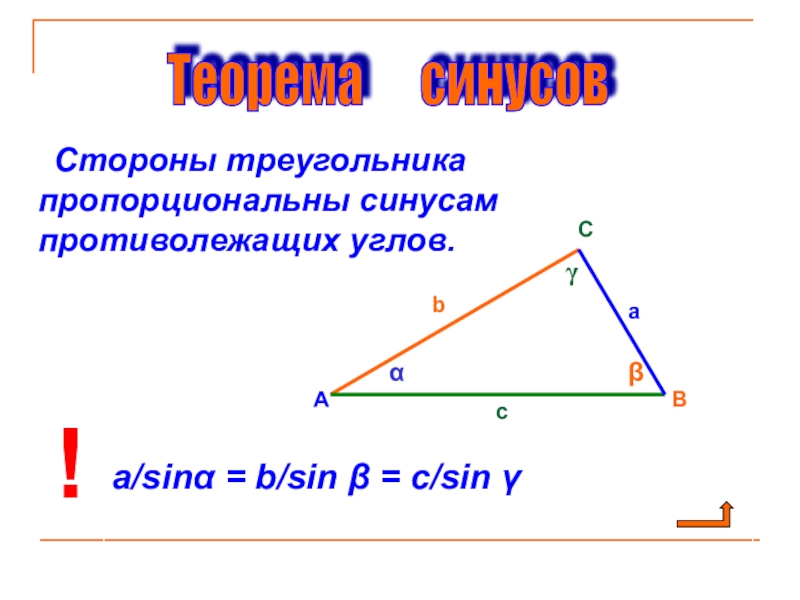
Слайд 7
Стороны треугольника пропорциональны синусам противолежащих углов.
A
B
b
c
a
γ
α
β
a/sinα = b/sin β = c/sin γ
C
!
Теорема синусов
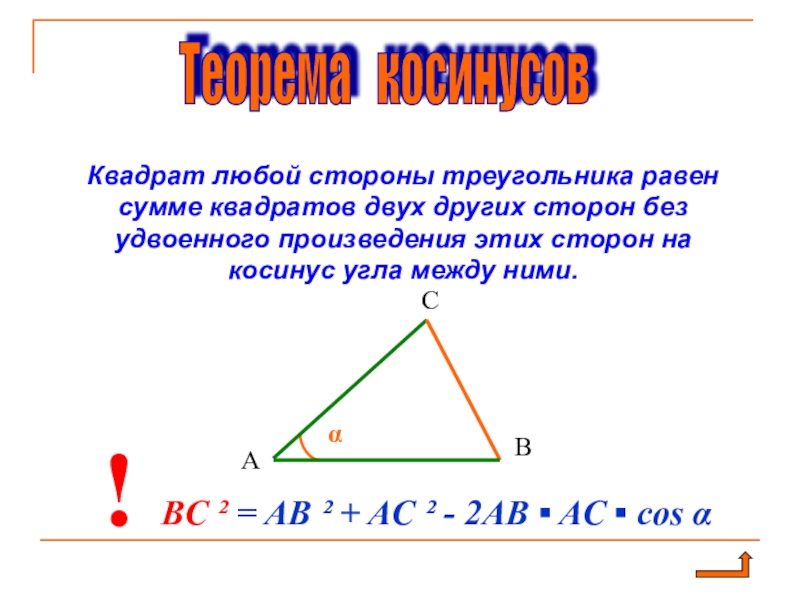
Слайд 8Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без
A
B
C
α
BC ² = AB ² + AC ² - 2AB ▪ AC ▪ cos α
!
Теорема косинусов
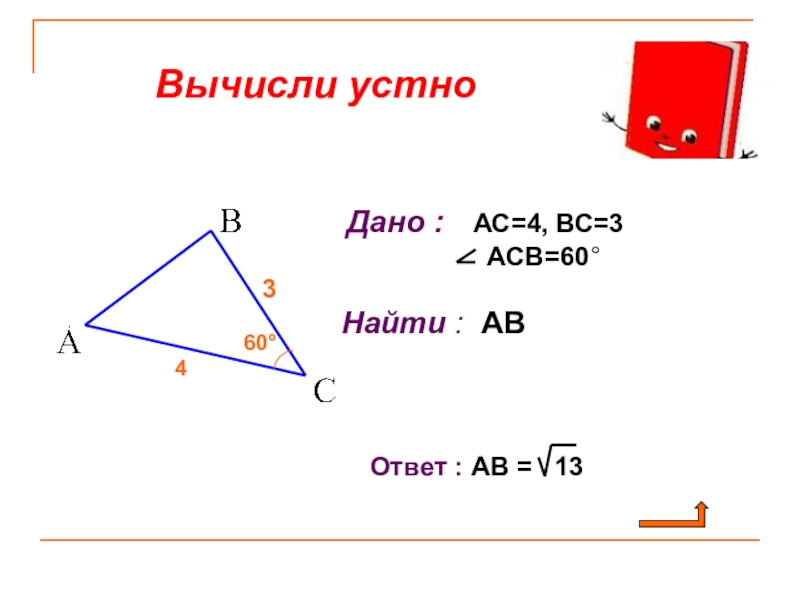
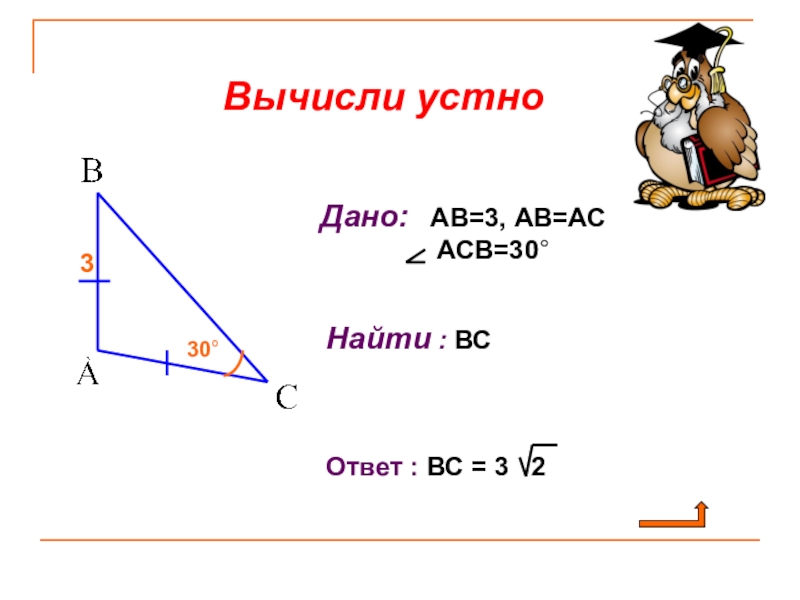
Слайд 9Соединить линиями части фраз, соответствующие
друг другу ( в треугольнике
Если cos E > 0, то треугольник DEF – прямоугольный.
Если cos E= 0, то треугольник DEF – тупоугольный.
Если cos E< 0, то треугольник DEF – остроугольный.
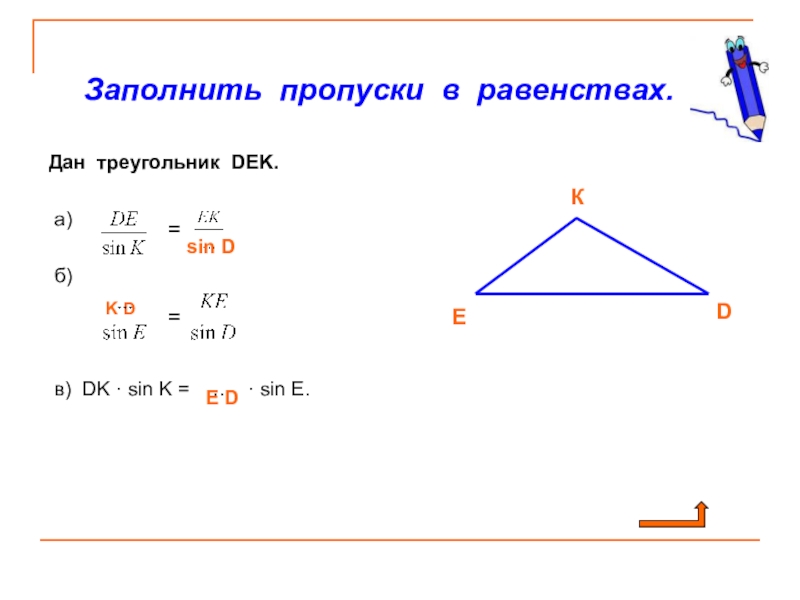
Слайд 10 Заполнить пропуски в равенствах.
Дан треугольник DEK.
а)
б)
в) DK · sin K = … · sin E.
sin D
K D
Е D
Е
К
D
=
=
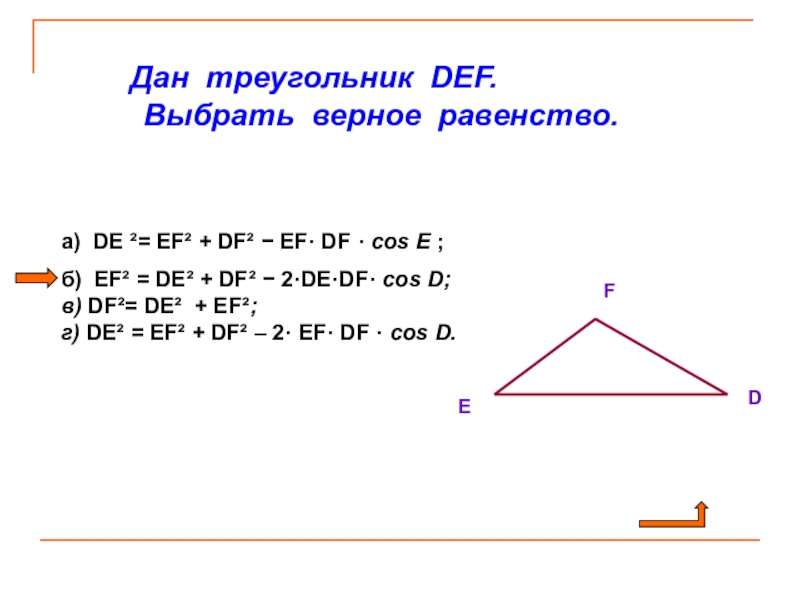
Слайд 11 Дан треугольник DEF.
а) DE ²= EF² + DF² − EF· DF · cos E ;
б) EF² = DE² + DF² − 2·DE·DF· cos D;
в) DF²= DE² + EF²;
г) DE² = EF² + DF² – 2· EF· DF · cos D.
Е
F
D
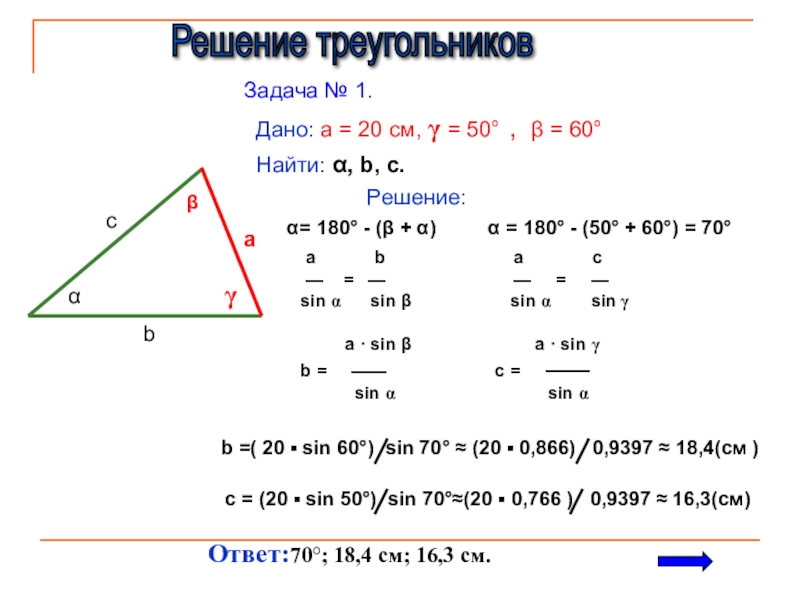
Слайд 15Решение треугольников
Задача № 1.
Дано: a = 20 см, γ =
Найти: α, b, c.
Решение:
α
β
γ
с
a
b
α= 180° - (β + α)
α = 180° - (50° + 60°) = 70°
b =( 20 ▪ sin 60°) sin 70° ≈ (20 ▪ 0,866) 0,9397 ≈ 18,4(см )
c = (20 ▪ sin 50°) sin 70°≈(20 ▪ 0,766 ) 0,9397 ≈ 16,3(см)
Ответ:70°; 18,4 см; 16,3 см.
а b а c
— = — — = —
sin α sin β sin α sin γ
a · sin β a · sin γ
b = —— c = ——
sin α sin α
Слайд 16Решение треугольников
α
β
γ
c
a
b
Дано:
a = 7 см,
b = 2 см,
c = 8 см
Найти:
α, β, γ
Решение:
cos α = (b ² + c ² - a ²) (2 ▪ b ▪ c)
cos α = (4 + 64 – 49) (2 ▪ 2 ▪ 8 ) ≈ 0,5938
α ≈ 53°34′
cos β = (a ² + c ² - b ²) (2 ▪ a ▪ c)
β ≈ 13°18′
γ = 180° - (α + β) ; γ = 180° - (53°34′ + 13°18′) = 113°08′
Ответ: 53°34′ ; 13°18′ ; 113°08′.
cos β = (49 + 64 – 4) ( 2 ▪ 7 ▪ 8 ) ≈ 0,9732
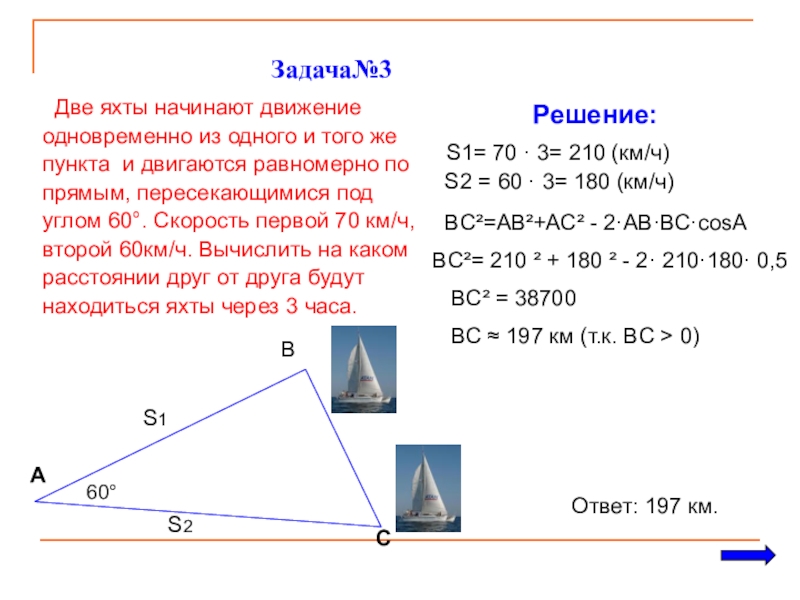
Слайд 17 Задача№3
Две
одновременно из одного и того же
пункта и двигаются равномерно по
прямым, пересекающимися под
углом 60°. Скорость первой 70 км/ч,
второй 60км/ч. Вычислить на каком
расстоянии друг от друга будут
находиться яхты через 3 часа.
Решение:
S1= 70 · 3= 210 (км/ч)
S2 = 60 · 3= 180 (км/ч)
A
B
C
60°
S1
S2
BС²=АВ²+АС² - 2·АВ·ВС·cosА
BС²= 210 ² + 180 ² - 2· 210·180· 0,5
BС² = 38700
BС ≈ 197 км (т.к. BС > 0)
Ответ: 197 км.
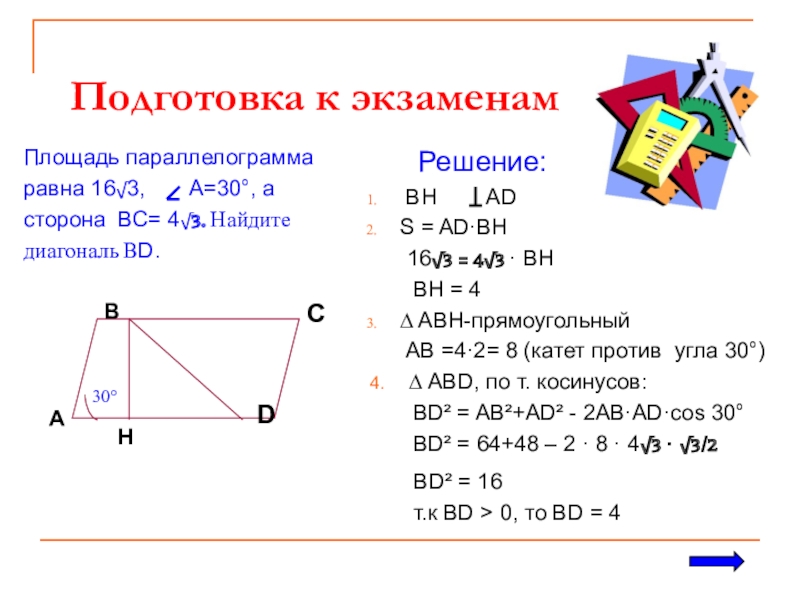
Слайд 18 Подготовка к экзаменам
Площадь параллелограмма
равна 16√3, А=30°,
сторона ВС= 4√3. Найдите
диагональ ВD.
Решение:
ВH АD
S = AD·BH
16√3 = 4√3 · BH
BH = 4
∆ ABH-прямоугольный
AB =4·2= 8 (катет против угла 30°)
4. ∆ ABD, по т. косинусов:
BD² = AB²+AD² - 2AB·AD·cos 30°
BD² = 64+48 – 2 · 8 · 4√3 · √3/2
A
H
B
C
D
BD² = 16
т.к BD > 0, то BD = 4
30°
Слайд 19 Физкультминутка
Мудра Жизни.
Мудра Знания.
Указательный палец
Подушечки мизинца, безымянного и большого
пальцев каждой руки соедините вместе, средние и указательные
пальцы держите выпрямленными.
Слайд 20 Тест
Герберт Спенсер, английский философ, говорил: «Дороги не те знания, которые
Слайд 21
1. Выбери верное утверждение:
а) Квадрат любой стороны треугольника равен сумме
квадратов двух других его сторон;
б) Квадрат любой стороны треугольника равен сумме
квадратов двух других сторон без удвоенного
произведения этих сторон на косинус угла между ними;
в) Квадрат любой стороны треугольника равен сумме
квадратов двух других сторон, минус произведение
этих сторон на косинус угла между ними.
2. Для данного треугольника справедливо равенство…
а) sin α : a = sin γ : b б) sin γ: a = sin α : b
в) a: b = sin α : sin γ г) не ответа
3. В треугольнике CDE известны длины сторон
CD и CE . Величину какого угла
необходимо знать, чтобы найти длину стороны DE?
а) ∠ C, б) ∠ D, в) ∠ E.
4. Стороны треугольника 5 см и 4 см, а угол между ними равен 30°. Найти третью сторону треугольника.
а) √7 см б) √3 см в) 5 см; г) 3 см.
5. Определить вид треугольника со сторонами
5, 6 и 7 см.
а) остроугольный; б) равнобедренный;
в) тупоугольный; г) прямоугольный.
Вариант 2.
1. Выбери верное утверждение:
а) Стороны треугольника пропорциональны синусам
противолежащих углов;
б) Стороны треугольника обратно пропорциональны
синусам противолежащих углов;
в) Стороны треугольника пропорциональны синусам прилежащих углов.
2. Для данного треугольника справедливо равенство…
а) a² = b²+ c² - b ·c ·cos α б) b²= a² + c² - 2 а · с· cos β
в) a² = b²+ c² - 2 b ·c · cos β г) нет ответа
3. В треугольнике MNK известны длины сторон
MN и NK . Величину какого угла необходимо знать, чтобы найти длину стороны MK?
а) ∠ M, б) ∠ N, в) ∠ K.
4. Стороны треугольника 5 см и 3 см, а угол между ними 60°. Найдите третью сторону треугольника.
а) 2 см б) √23 см в) √19 см
г) 4,5 см.
5. Определить вид треугольника со сторонами 4, 6 и 9 см.
а) остроугольный; б) равнобедренный;
в) тупоугольный; г) прямоугольный.
Слайд 22 Ответы к тесту
1) б
2) г
3) а
4) г
_____________
5) а
2 вариант
1) а
2) б
3) б
4) в
________________
5) в