- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Построение сечений в пирамиде
Содержание
- 1. Презентация по геометрии на тему Построение сечений в пирамиде
- 2. Содержание:О задачах на построение сечений Подготовительные задачи Алгоритм
- 3. Для построения прямой пересечения двух плоскостей достаточно
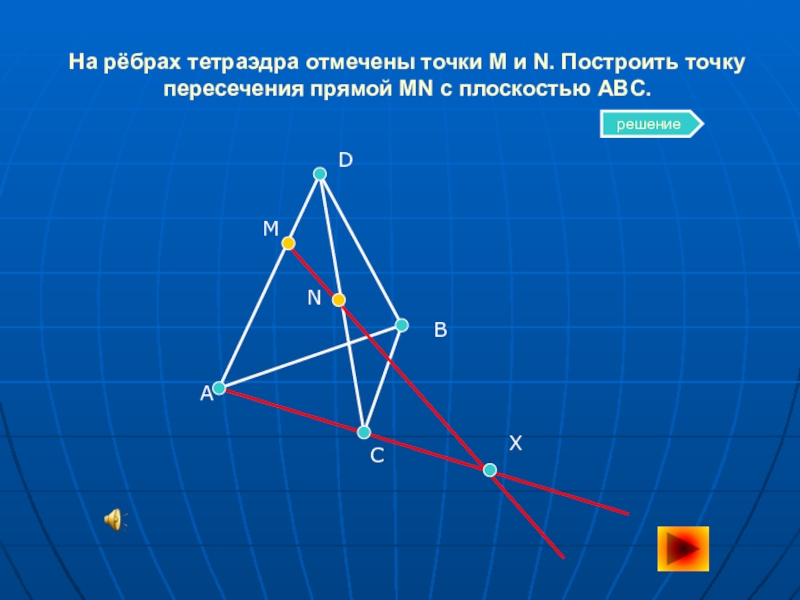
- 4. На рёбрах тетраэдра отмечены точки M и N. Построить точку пересечения прямой MN с плоскостью ABC.ACBDMNXрешение
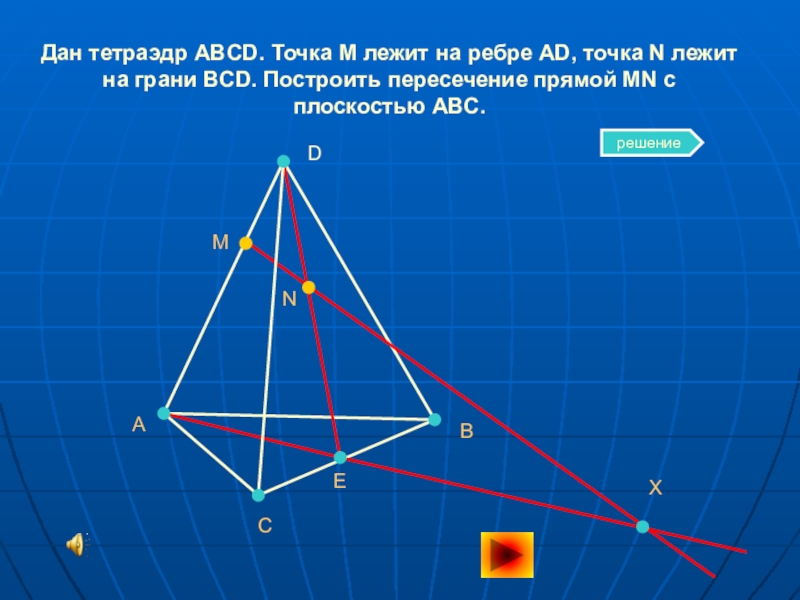
- 5. Дан тетраэдр ABCD. Точка M лежит на
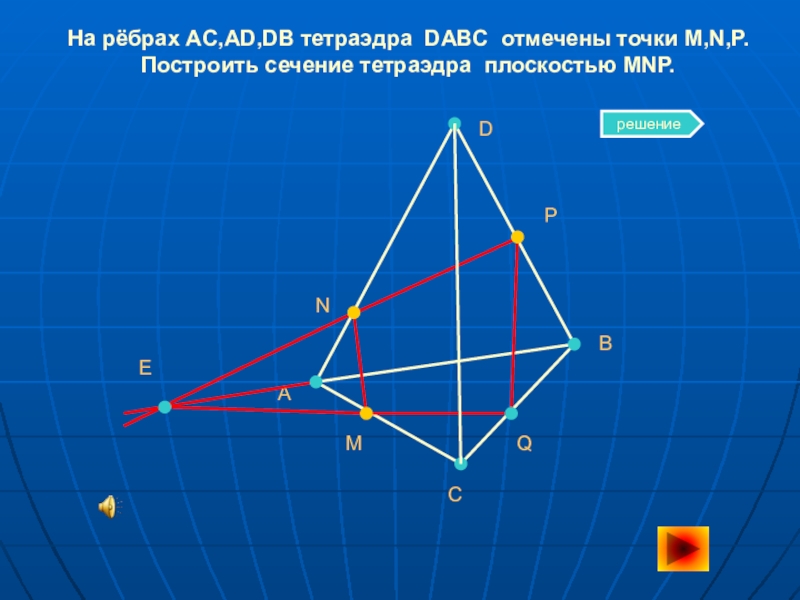
- 6. На рёбрах AC,AD,DB тетраэдра DABC отмечены точки M,N,P. Построить сечение тетраэдра плоскостью MNP.АСВDNMPЕQрешение
- 7. Сформулируем алгоритм построения сечений призм и
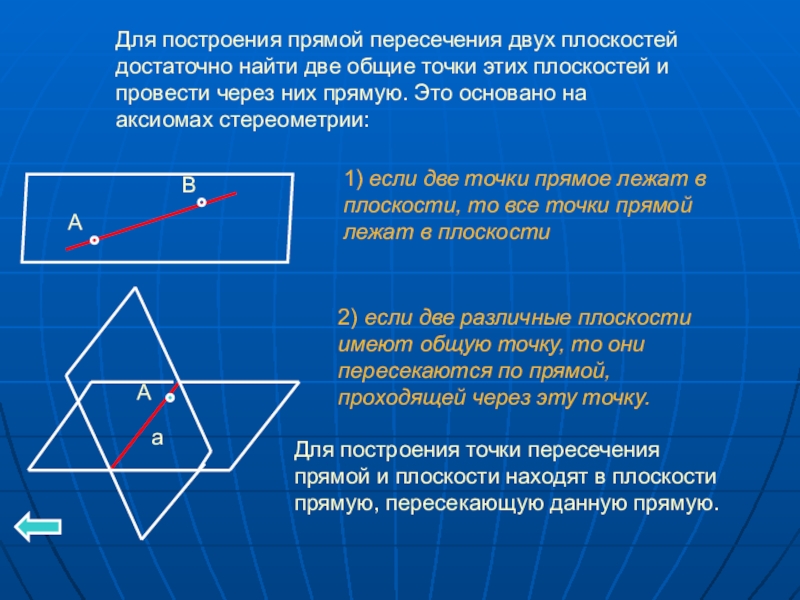
Слайд 3Для построения прямой пересечения двух плоскостей достаточно найти две общие точки
1) если две точки прямое лежат в плоскости, то все точки прямой лежат в плоскости
2) если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Для построения точки пересечения прямой и плоскости находят в плоскости прямую, пересекающую данную прямую.
Слайд 4На рёбрах тетраэдра отмечены точки M и N. Построить точку пересечения
A
C
B
D
M
N
X
решение
Слайд 5Дан тетраэдр ABCD. Точка M лежит на ребре AD, точка N
A
C
B
D
M
N
Е
X
решение
Слайд 6На рёбрах AC,AD,DB тетраэдра DABC отмечены точки M,N,P. Построить сечение тетраэдра
А
С
В
D
N
M
P
Е
Q
решение
Слайд 7
Сформулируем алгоритм построения сечений призм и пирамид по трем
Шаг 1. Строим проекции M 1 ,N1, K1 данных точек M, N, K на плоскость основания (параллельно боковым ребрам в случае призм и из вершины пирамиды как из центра проекции в случае пирамид); эту плоскость называют основной.
Шаг 2. Пересекая прямые, соединяющие данные точки с их проекциями, находим точки пересечения этих прямых с основной плоскостью. Проходящая через них прямая есть след сечения на основании. Чтобы ее провести, достаточно найти хотя бы две ее точки.
Шаг 3. Находим точки пересечения следа со сторонами основания или их продолжениями. Используя эти точки и те из данных точек, которые лежат на боковой поверхности многогранника, последовательно находим вершины сечения на боковых ребрах, а в случае призмы – и на сторонах второго основания.