- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Определение пирамиды
Содержание
- 1. Презентация по геометрии на тему Определение пирамиды
- 2. - Давайте вспомним, что называется геометрическим телом?Геометрическим
- 3. Слайд 3
- 4. Слайд 4
- 5. -Как называются фигуры, которые мы с вами
- 6. Давайте рассмотрим с вами тетраэдрУ тетраэдра есть
- 7. -Из каких фигур состоит тетраэдр?Тетраэдр состоит из
- 8. -Из каких фигур состоит данный многогранник?Он состоит
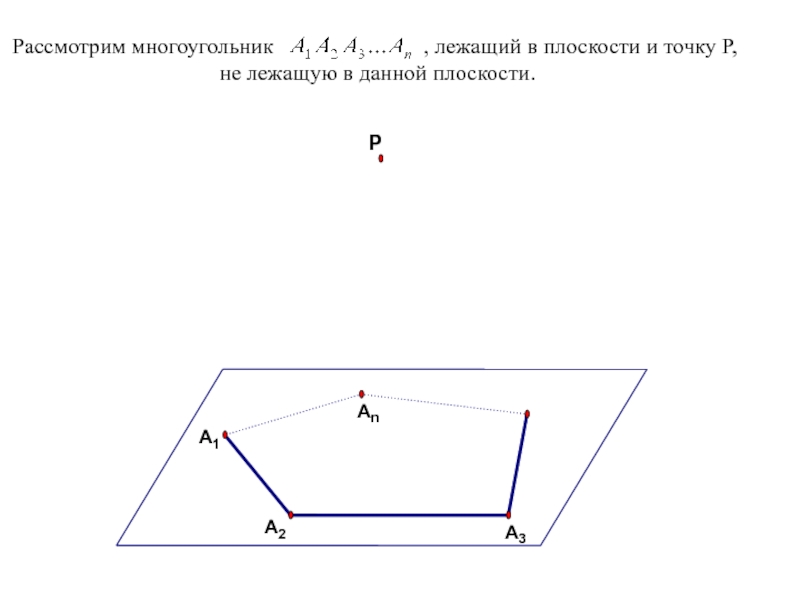
- 9. Рассмотрим многоугольник
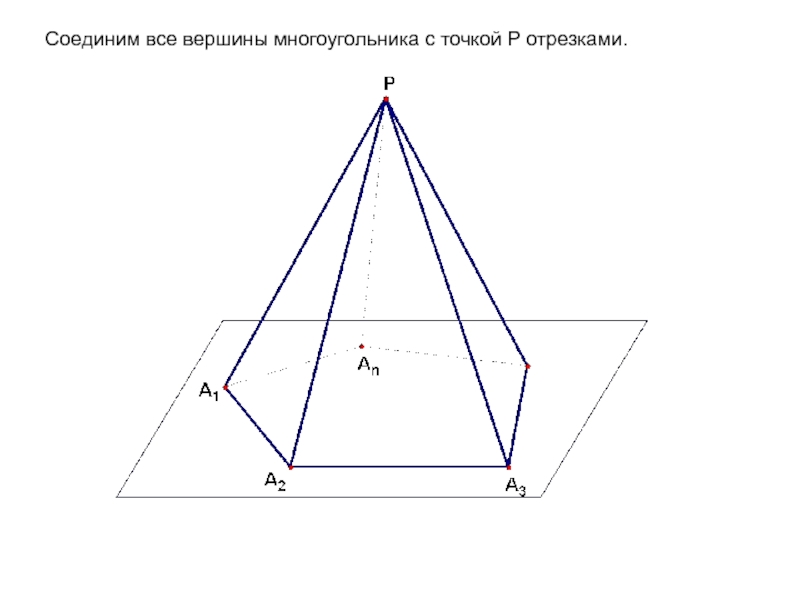
- 10. Соединим все вершины многоугольника с точкой P отрезками.
- 11. -Какое название вы бы могли дать построенному
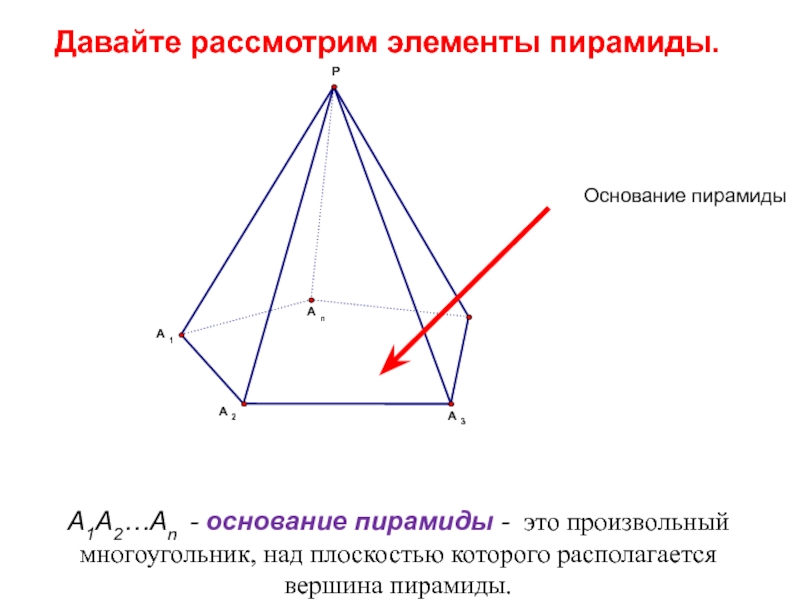
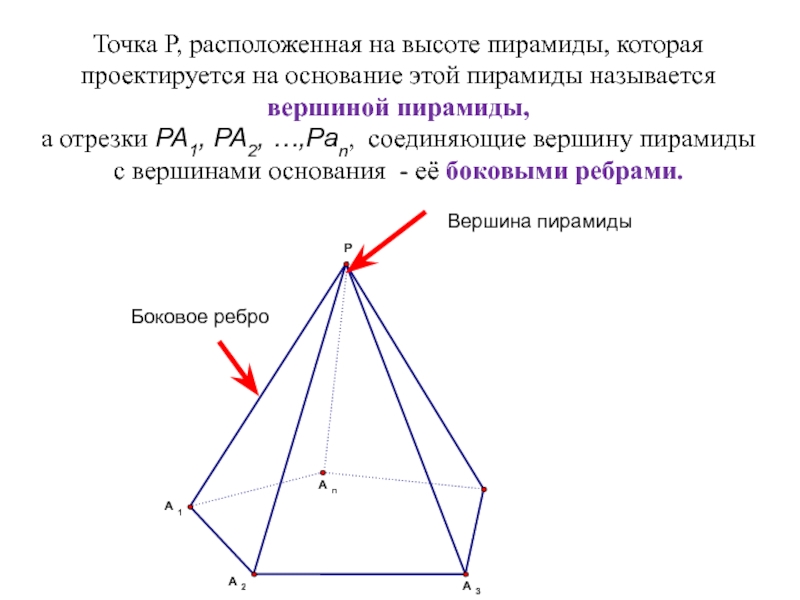
- 12. Давайте рассмотрим элементы пирамиды.A1A2…An - основание пирамиды
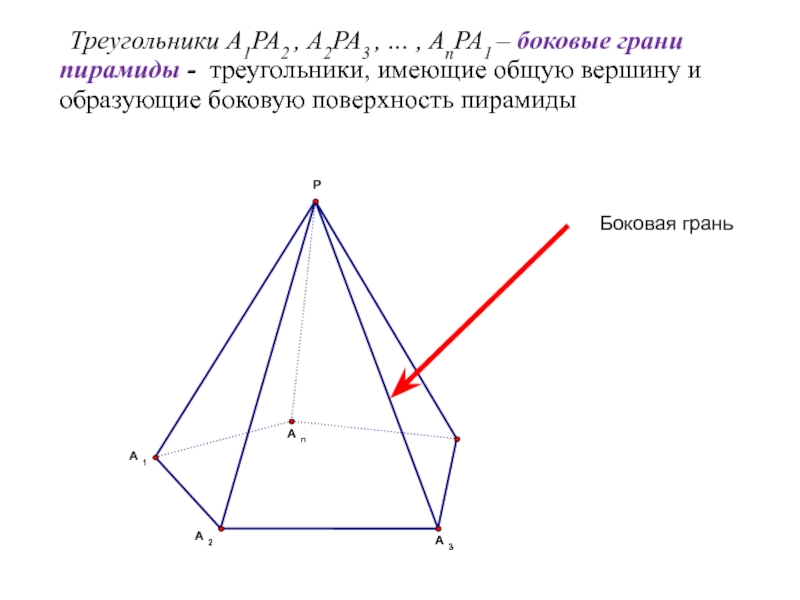
- 13. Треугольники A1PA2 , A2PA3 , … ,
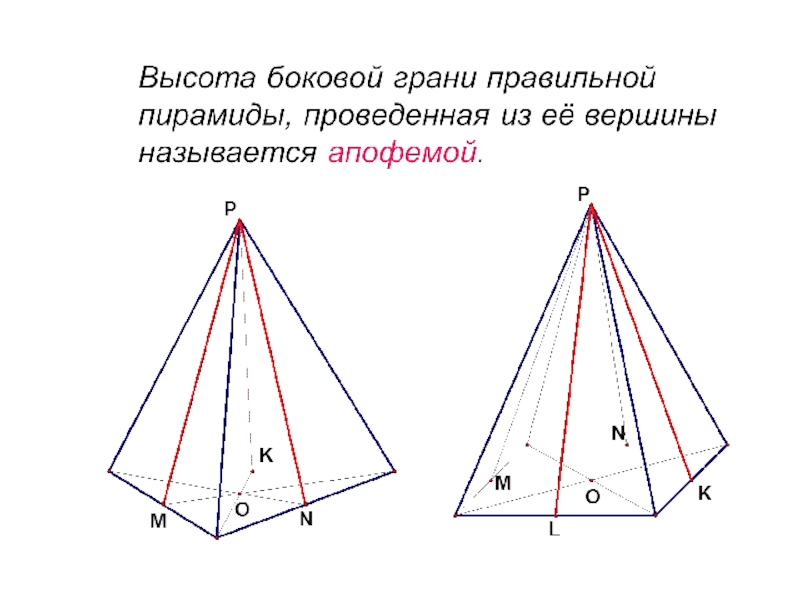
- 14. Точка P, расположенная на высоте пирамиды, которая
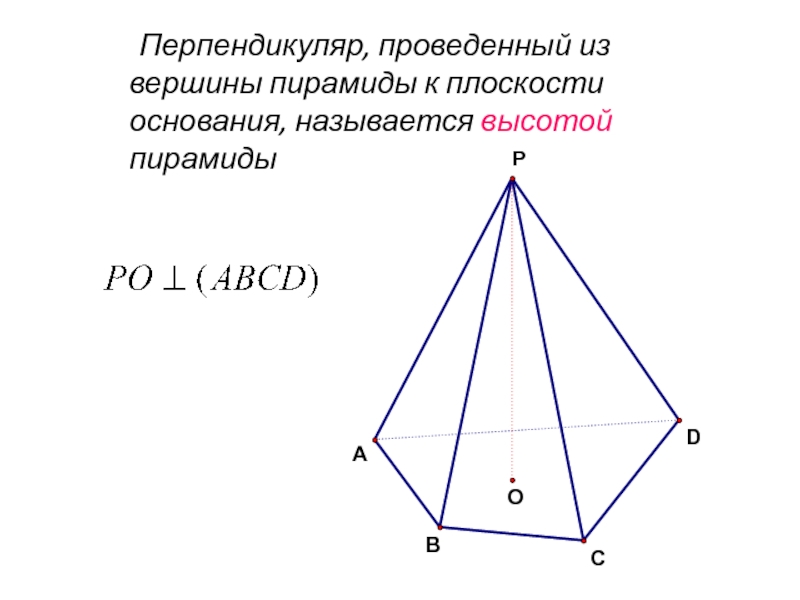
- 15. Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамидыPDCBAO
- 16. Давайте рассмотрим виды пирамид, их свойства и формулы.
- 17. Слайд 17
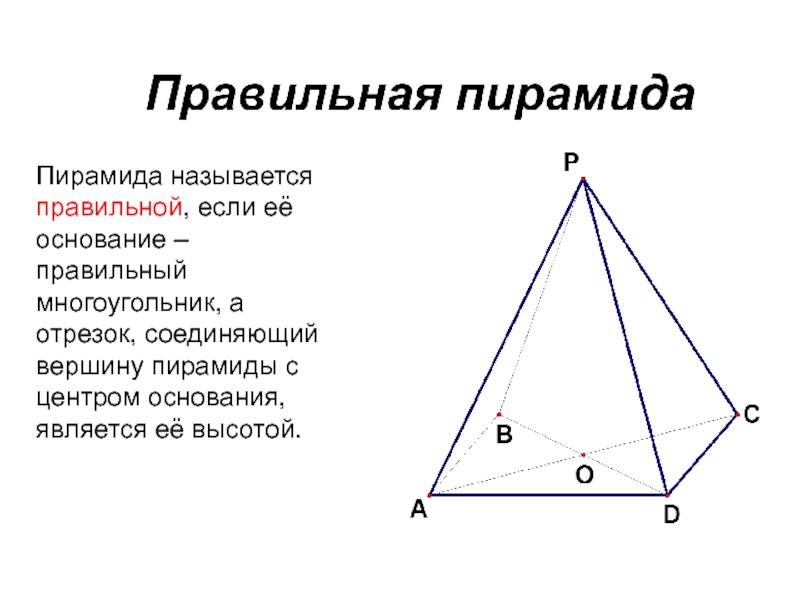
- 18. Пирамида называется правильной, если её основание –
- 19. Слайд 19
- 20. Слайд 20
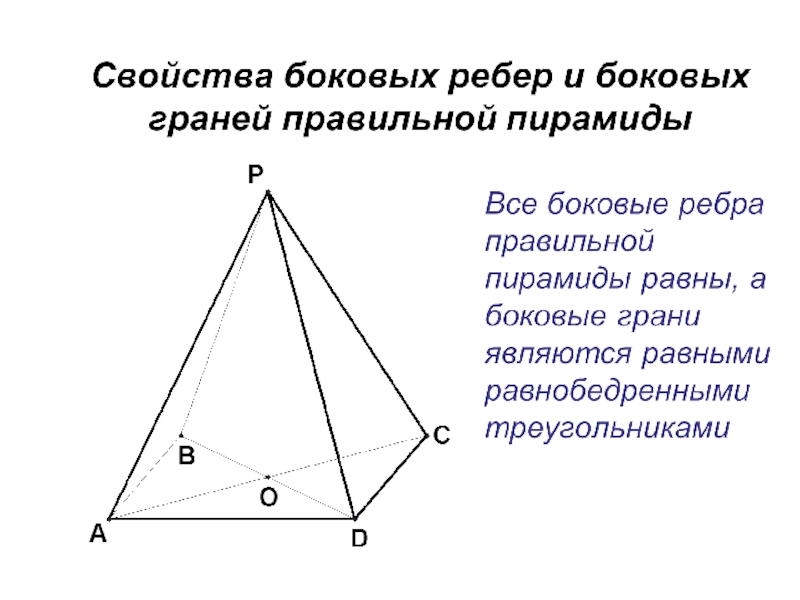
- 21. Правильная пирамида основание – правильный многоугольник, вершина
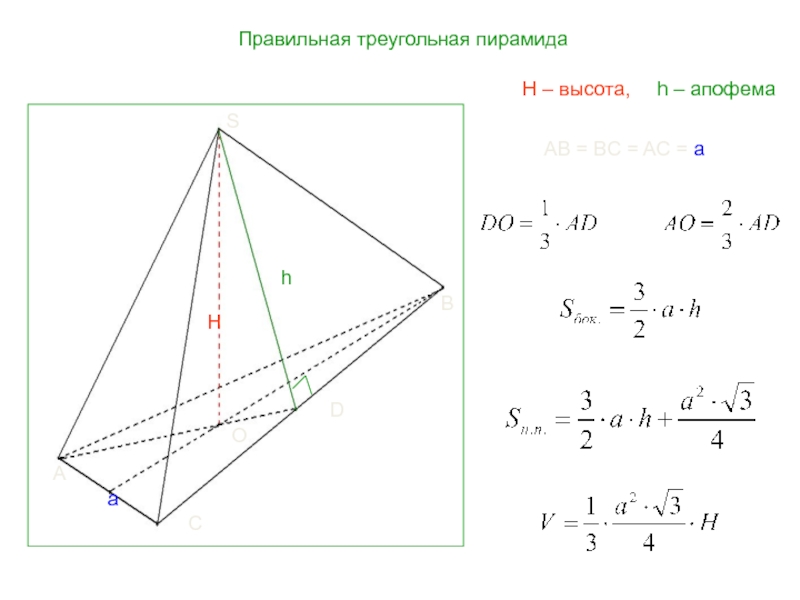
- 22. AB = BC = AC = aПравильная треугольная пирамидаH – высота, h – апофема AOBChHSDa
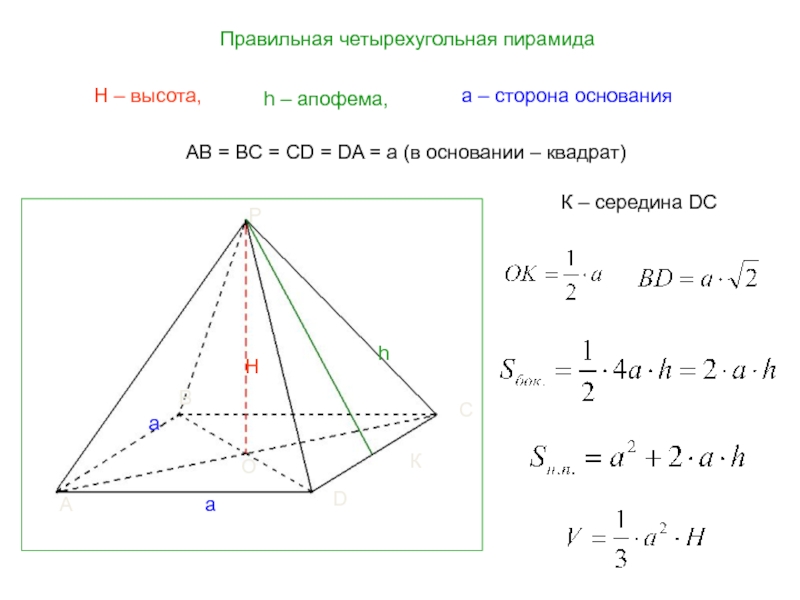
- 23. Правильная четырехугольная пирамидаh – апофема, H –
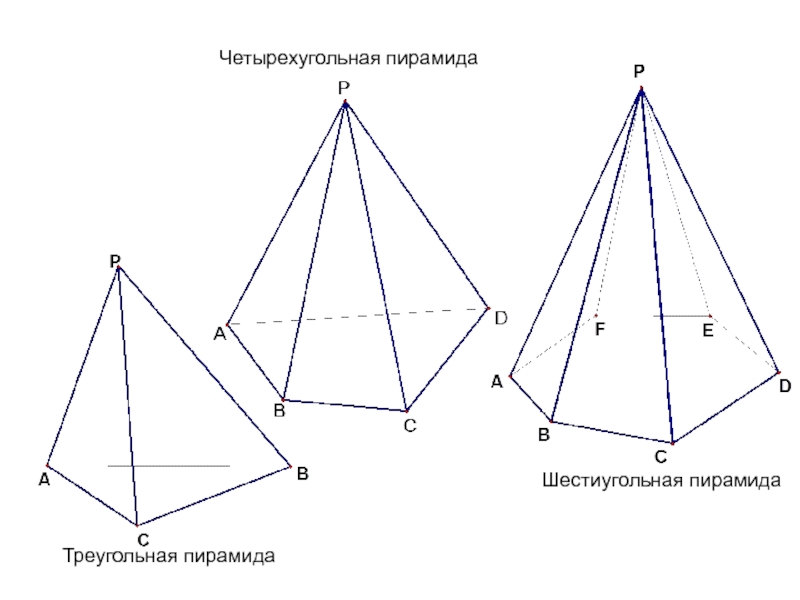
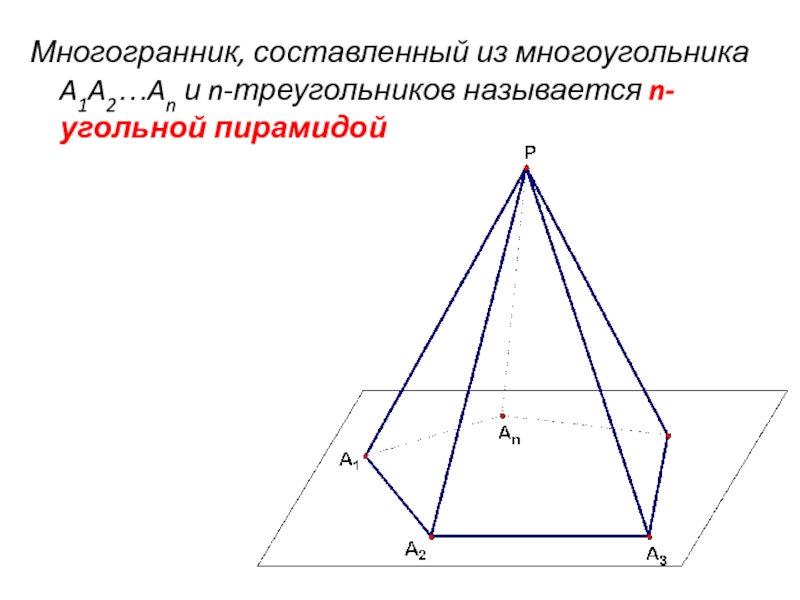
- 24. Многогранник, составленный из многоугольника A1A2…An и n-треугольников называется n-угольной пирамидой
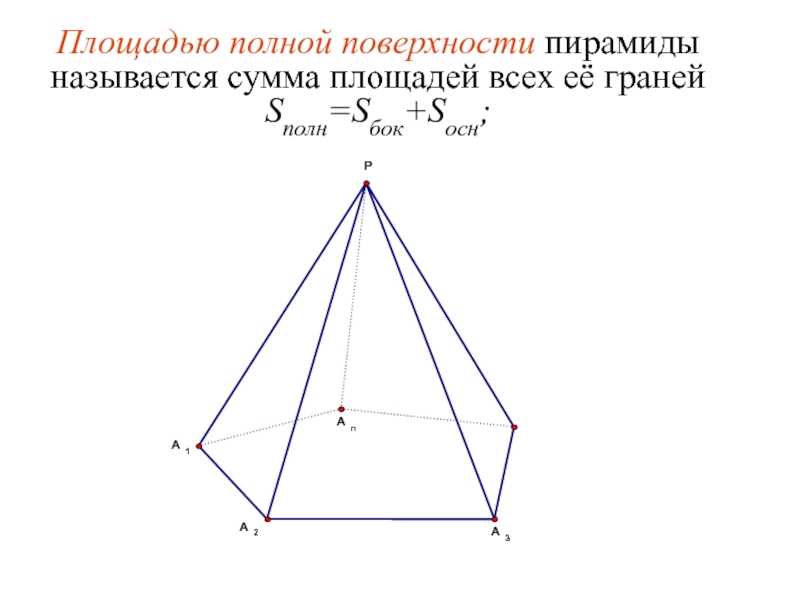
- 25. Площадью полной поверхности пирамиды называется сумма площадей всех её гранейSполн=Sбок+Sосн;
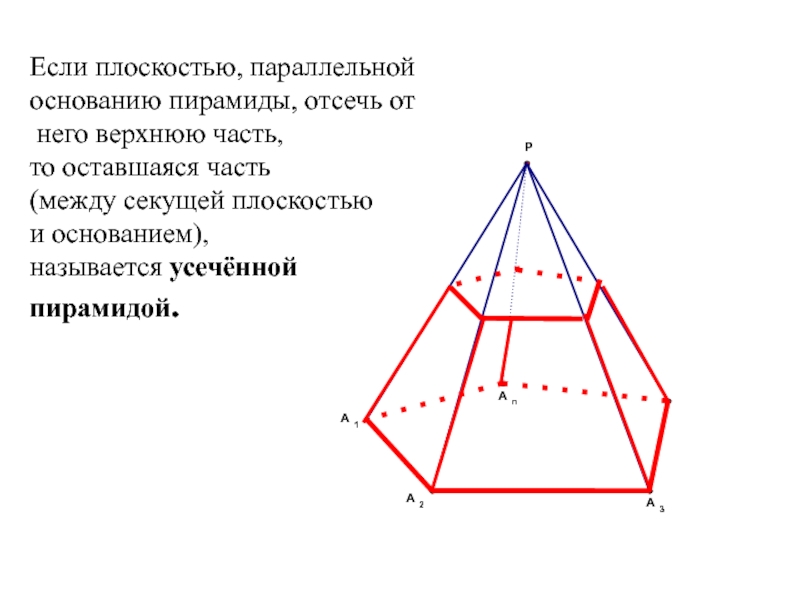
- 26. Если плоскостью, параллельной основанию пирамиды, отсечь
- 27. PA1A2…An – произвольная пирамидаα – плоскость основанияβ
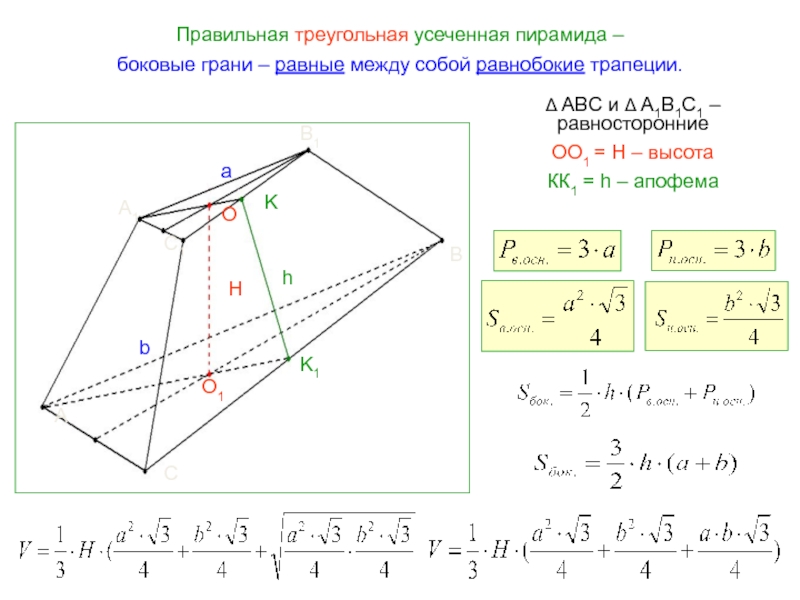
- 28. Правильная треугольная усеченная пирамида – боковые грани
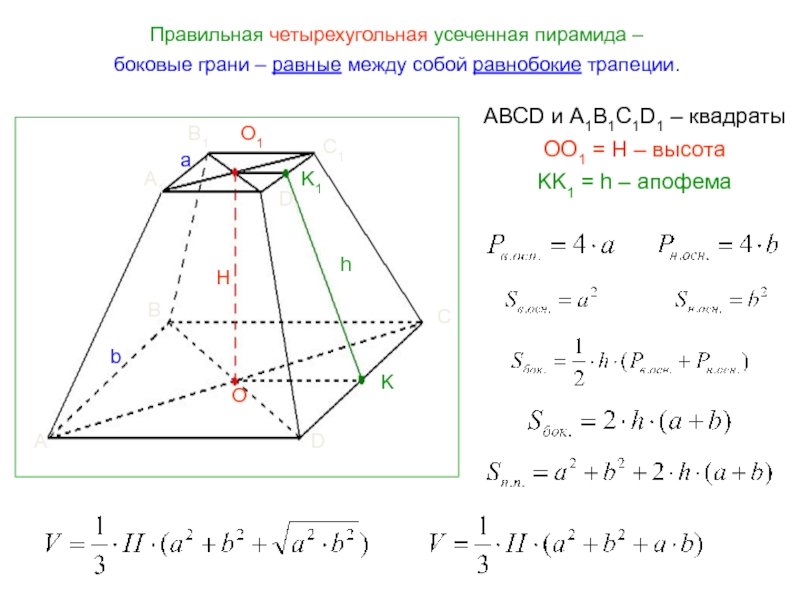
- 29. Правильная четырехугольная усеченная пирамида – боковые грани
- 30. Пирамиды в жизни
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
- 38. 1. Сколько боковых рёбер у пятиугольной пирамиды?4
- 39. Ответы:Правильный ответ 3).Правильный ответ 1).Правильный ответ 3).Правильный ответ 2).Правильный ответ 1).
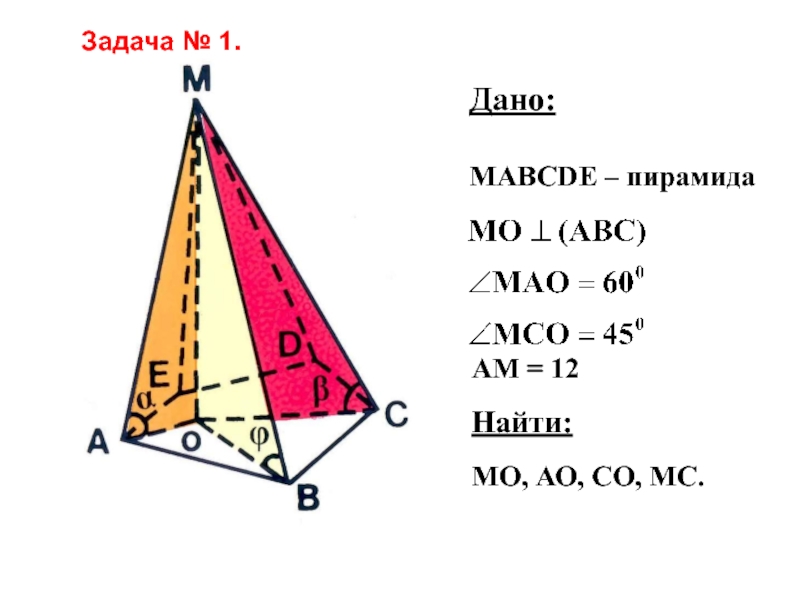
- 40. Дано:МАВСDЕ – пирамидаАМ = 12Найти:МО, АО, СО, МС.Задача № 1.
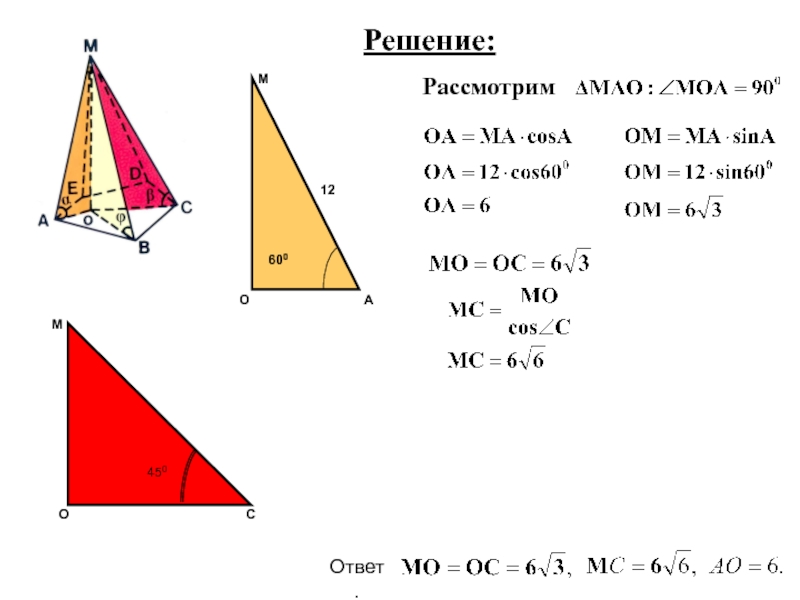
- 41. Решение:Рассмотрим Ответ.
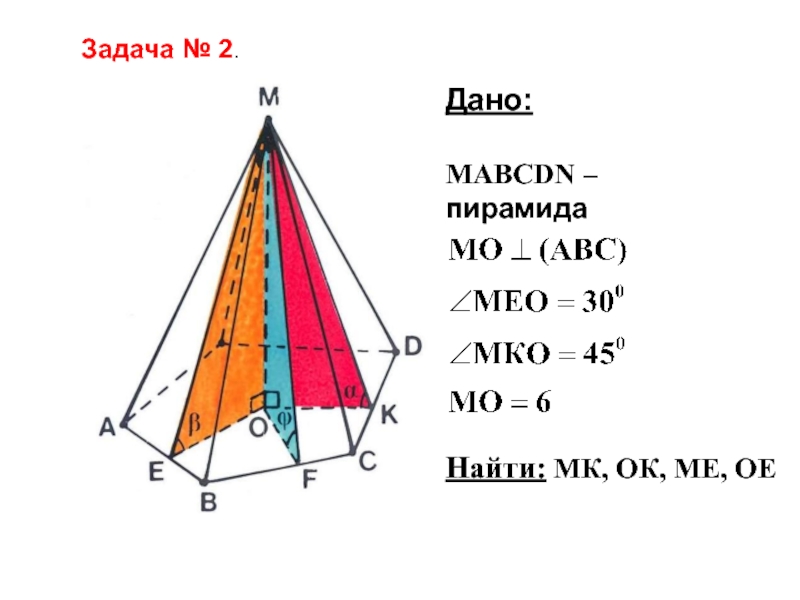
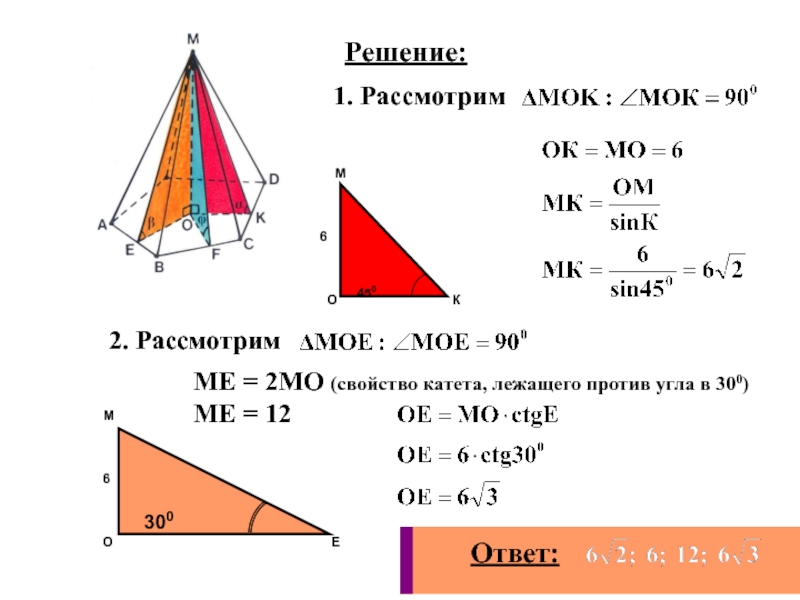
- 42. Дано:МАВСDN – пирамидаНайти: МК, ОК, МЕ, ОЕЗадача № 2.
- 43. Решение:1. Рассмотрим 2. Рассмотрим МЕ = 2МО (свойство катета, лежащего против угла в 300)МЕ = 12
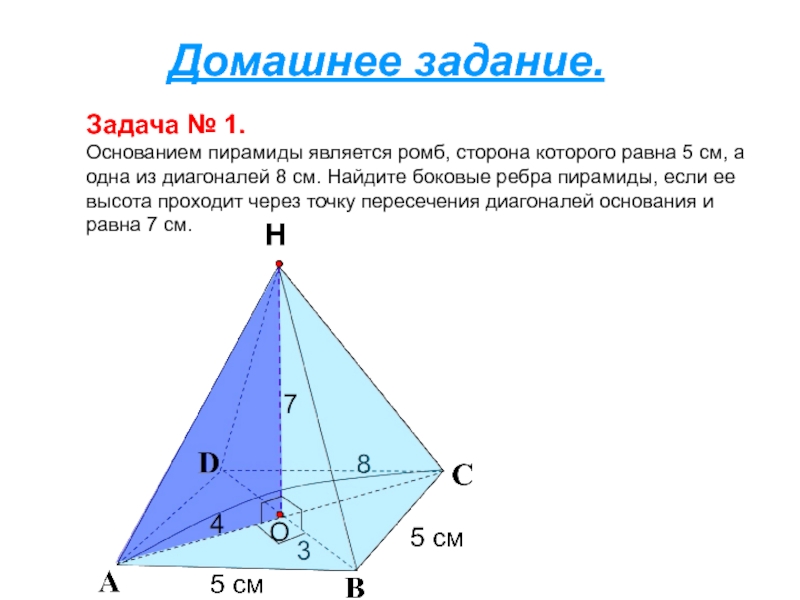
- 44. Домашнее задание.Задача № 1.Основанием пирамиды является ромб,
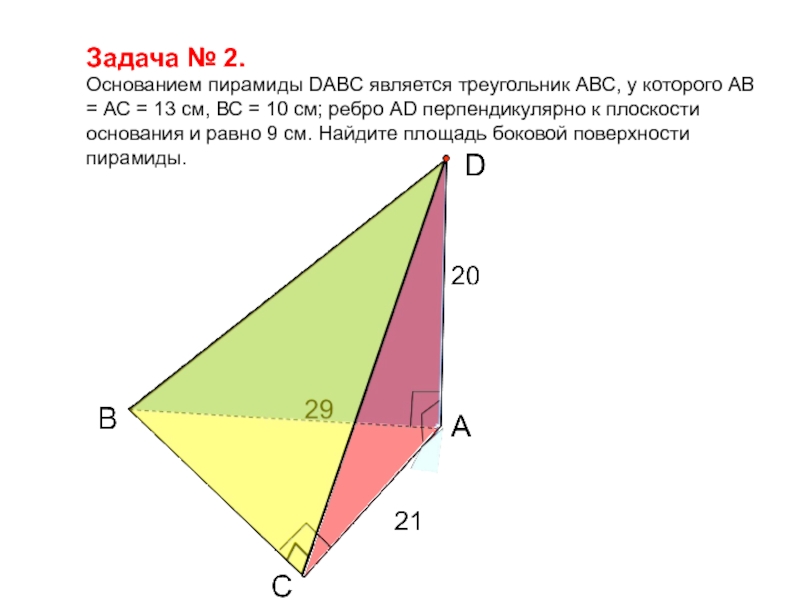
- 45. Задача № 2.Основанием пирамиды DАВС является треугольник
- Давайте вспомним, что называется геометрическим телом?Геометрическим телом - называют ограниченную фигуру в пространстве, которая содержит все свои граничные точки, причем сколь угодно близко от любой граничной точки находятся внутренние точки фигуры.Какие геометрические тела вы знаете?-Призма,
Слайд 2- Давайте вспомним, что называется геометрическим телом?
Геометрическим телом - называют ограниченную
фигуру в пространстве, которая содержит все свои граничные точки, причем сколь угодно близко от любой граничной точки находятся внутренние точки фигуры.
Какие геометрические тела вы знаете?
-Призма, куб, параллелепипед, тетраэдр, октаэдр.
- Давайте изобразим каждую из фигур:
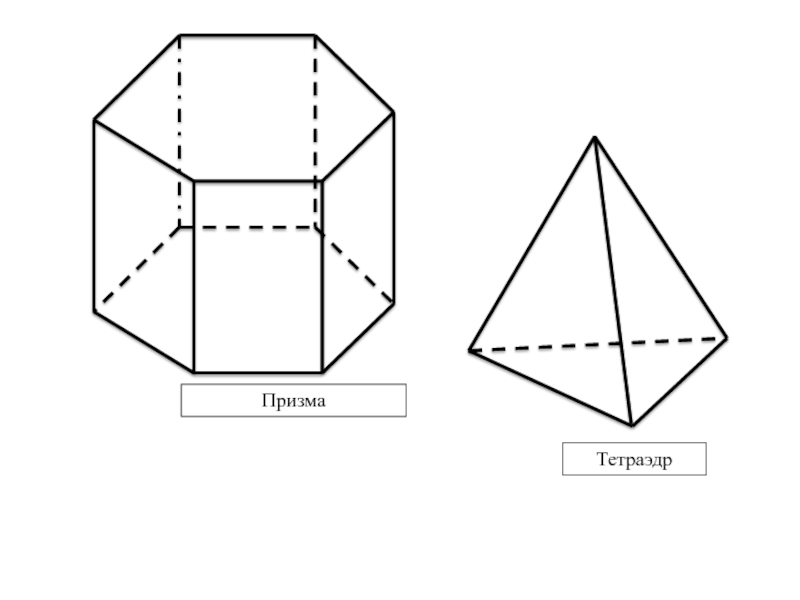
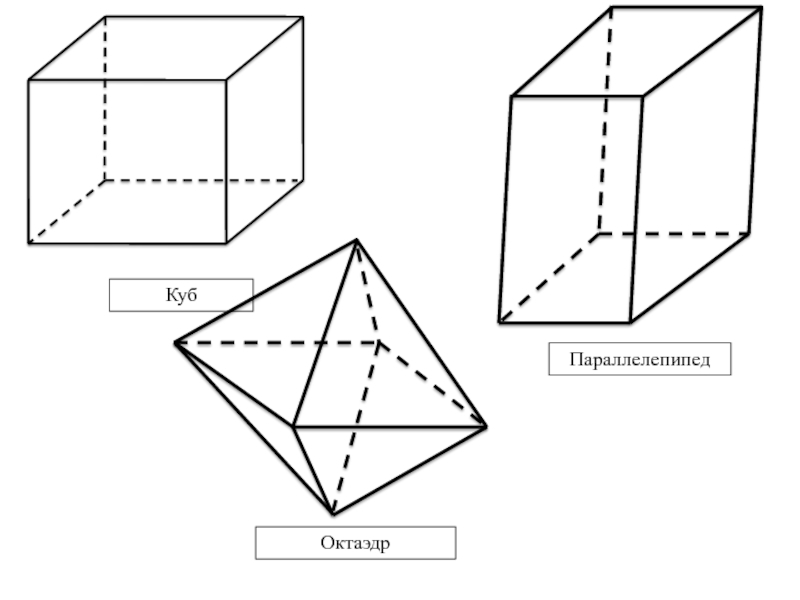
Какие геометрические тела вы знаете?
-Призма, куб, параллелепипед, тетраэдр, октаэдр.
- Давайте изобразим каждую из фигур:
Слайд 5-Как называются фигуры, которые мы с вами только что вспомнили и
изобразили?
-Эти фигуры называются многогранниками.
-Что называется многогранником?
Многогранником называется поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело.
Давайте рассмотрим тетраэдр и вспомним все его характеристики.
-Эти фигуры называются многогранниками.
-Что называется многогранником?
Многогранником называется поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело.
Давайте рассмотрим тетраэдр и вспомним все его характеристики.
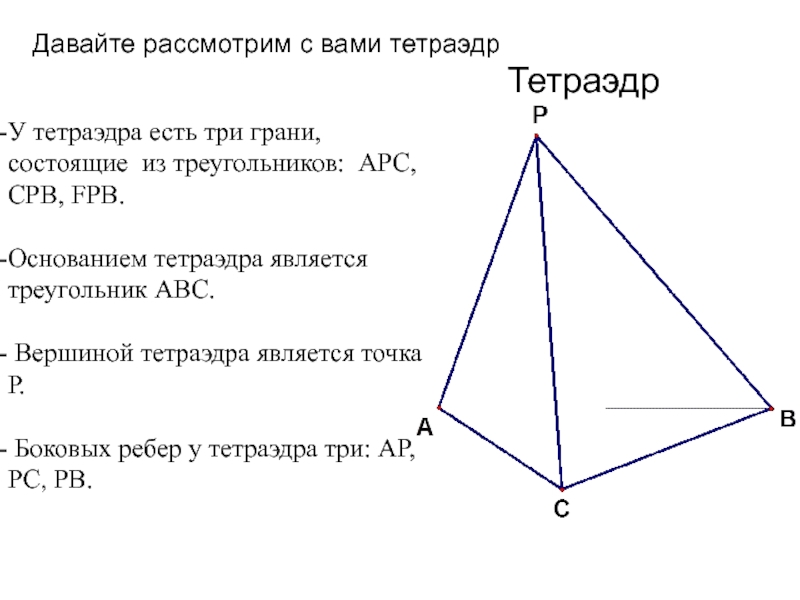
Слайд 6Давайте рассмотрим с вами тетраэдр
У тетраэдра есть три грани, состоящие из
треугольников: АPC, CPB, FPB.
Основанием тетраэдра является треугольник АВС.
Вершиной тетраэдра является точка Р.
Боковых ребер у тетраэдра три: АР, РС, РВ.
Основанием тетраэдра является треугольник АВС.
Вершиной тетраэдра является точка Р.
Боковых ребер у тетраэдра три: АР, РС, РВ.
Слайд 7-Из каких фигур состоит тетраэдр?
Тетраэдр состоит из одних треугольников.
Сколько треугольников
входит в состав тетраэдра?
Четыре треугольника.
Что является основанием тетраэдра?
Треугольник.
А остальные три треугольника чем являются для тетраэдра?
Боковыми гранями.
Давайте попробуем изобразить фигуру, в основании которой будет лежать четырехугольник.
Четыре треугольника.
Что является основанием тетраэдра?
Треугольник.
А остальные три треугольника чем являются для тетраэдра?
Боковыми гранями.
Давайте попробуем изобразить фигуру, в основании которой будет лежать четырехугольник.
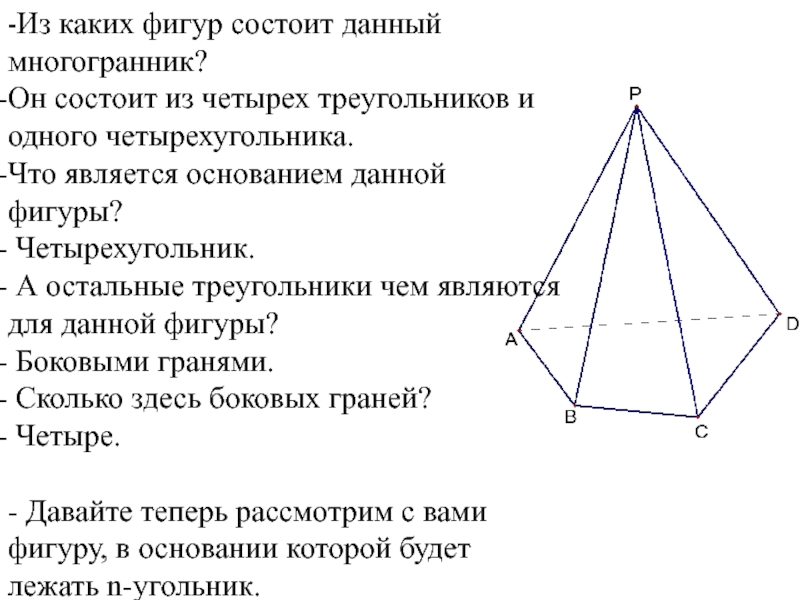
Слайд 8-Из каких фигур состоит данный многогранник?
Он состоит из четырех треугольников и
одного четырехугольника.
Что является основанием данной фигуры?
Четырехугольник.
А остальные треугольники чем являются для данной фигуры?
Боковыми гранями.
Сколько здесь боковых граней?
Четыре.
- Давайте теперь рассмотрим с вами фигуру, в основании которой будет лежать n-угольник.
Что является основанием данной фигуры?
Четырехугольник.
А остальные треугольники чем являются для данной фигуры?
Боковыми гранями.
Сколько здесь боковых граней?
Четыре.
- Давайте теперь рассмотрим с вами фигуру, в основании которой будет лежать n-угольник.
Слайд 11-Какое название вы бы могли дать построенному телу?
- Пирамида.
Давайте дадим определение,
какое именно тело мы будем называть пирамидой.
- Пирамидой называется многогранник, в основании которого лежит многоугольник, а остальными гранями являются треугольники, имеющие общую вершину.
- Пирамидой называется многогранник, в основании которого лежит многоугольник, а остальными гранями являются треугольники, имеющие общую вершину.
Слайд 12Давайте рассмотрим элементы пирамиды.
A1A2…An - основание пирамиды - это произвольный многоугольник,
над плоскостью которого располагается вершина пирамиды.
Слайд 13 Треугольники A1PA2 , A2PA3 , … , AnPA1 – боковые грани
пирамиды - треугольники, имеющие общую вершину и образующие боковую поверхность пирамиды
Слайд 14Точка P, расположенная на высоте пирамиды, которая проектируется на основание этой
пирамиды называется вершиной пирамиды,
а отрезки PA1, PA2, …,Pan, соединяющие вершину пирамиды с вершинами основания - её боковыми ребрами.
а отрезки PA1, PA2, …,Pan, соединяющие вершину пирамиды с вершинами основания - её боковыми ребрами.
Слайд 15 Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды
P
D
C
B
A
O
Слайд 18Пирамида называется правильной, если её основание – правильный многоугольник, а отрезок,
соединяющий вершину пирамиды с центром основания, является её высотой.
Слайд 21Правильная пирамида
основание – правильный многоугольник, вершина проецируется в центр основания;
боковые ребра – равны;
боковые грани – равные равнобедренные треугольники.
боковые грани – равные равнобедренные треугольники.
H – высота,
h – апофема
H
h
Слайд 23Правильная четырехугольная пирамида
h – апофема,
H – высота,
AB = BC
= CD = DA = a (в основании – квадрат)
H
h
a
a
A
B
D
O
P
К
К – середина DC
C
а – сторона основания
Слайд 24Многогранник, составленный из многоугольника A1A2…An и n-треугольников называется n-угольной пирамидой
Слайд 25Площадью полной поверхности пирамиды называется сумма площадей всех её граней
Sполн=Sбок+Sосн;
Слайд 26Если плоскостью, параллельной основанию пирамиды, отсечь от него верхнюю часть, то
оставшаяся часть
(между секущей плоскостью
и основанием),
называется усечённой пирамидой.
P
Слайд 27PA1A2…An – произвольная пирамида
α – плоскость основания
β – секущая плоскость,
PB1B2…Bn
– пирамида
Усеченная пирамида
β
α
P
A1
A2
A3
An
B1
B3
Bn
B2
O
O1
H
B1B2…Bn – верхнее основание
A1A2…An – нижнее снование
A1B1B2A2; …; AnBnB1A1 – боковые грани – трапеции
A1B1; A2B2; …; AnBn – боковые ребра
OO1= H – высота
Слайд 28Правильная треугольная усеченная пирамида –
боковые грани – равные между собой
равнобокие трапеции.
Δ ABC и Δ A1B1C1 – равносторонние
OO1 = H – высота
КК1 = h – апофема
A
C
A1
B1
C1
O1
O
H
K1
K
h
B
a
b
Слайд 29Правильная четырехугольная усеченная пирамида –
боковые грани – равные между собой
равнобокие трапеции.
ABCD и A1B1C1D1 – квадраты
OO1 = H – высота
KK1 = h – апофема
A1
A
B
C
D
B1
C1
D1
O
O1
H
K
K1
h
a
b
Слайд 381. Сколько боковых рёбер у пятиугольной пирамиды?
4
6
5
2. Сколько граней
у шестиугольной пирамиды?
4. Какое наименьшее количество граней может быть у пирамиды?
5. Какое наименьшее количество ребер может быть у пирамиды?
3. Какая фигура является боковой гранью пирамиды?
«Проверь себя …»
7
6
8
3
4
5
6
3
5
квадрат
2) Трапеция
3) треугольник
Слайд 39Ответы:
Правильный ответ 3).
Правильный ответ 1).
Правильный ответ 3).
Правильный ответ 2).
Правильный ответ 1).
Слайд 43Решение:
1. Рассмотрим
2. Рассмотрим
МЕ = 2МО (свойство катета, лежащего против
угла в 300)
МЕ = 12
МЕ = 12
Слайд 44Домашнее задание.
Задача № 1.
Основанием пирамиды является ромб, сторона которого равна 5
см, а одна из диагоналей 8 см. Найдите боковые ребра пирамиды, если ее высота проходит через точку пересечения диагоналей основания и равна 7 см.
Слайд 45Задача № 2.
Основанием пирамиды DАВС является треугольник АВС, у которого АВ
= АС = 13 см, ВС = 10 см; ребро АD перпендикулярно к плоскости основания и равно 9 см. Найдите площадь боковой поверхности пирамиды.
