- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Многогранники.
Содержание
- 1. Презентация по геометрии на тему Многогранники.
- 2. Определение: выпуклый многогранник называется правильным, если все
- 3. Тетраэдр Тетраэдр составлен из четырех равносторонних треугольников.
- 4. Гексаэдр (Куб) Куб составлен из шести квадратов.
- 5. Октаэдр Октаэдр составлен из восьми равносторонних треугольников.
- 6. ДодекаэдрДодекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая
- 7. ИкосаэдрИкосаэдр составлен из двадцати равносторонних треугольников. Каждая
- 8. Кроме правильных, существует тринадцать многогранников, которые впервые
- 9. Ромбокубооктаэдр. Его поверхность состоит из граней куба
- 10. Кубооктаэдр — полуправильный многогранник, состоящий из 14 граней
- 11. Ромбоикосододекаэдр —полуправильный многогранник, состоящий из 12 правильных ятиугольников,
- 12. Другие Архимедовы телаРомбоусечённый икосододекаэдрРомбоусечённый кубооктаэдр Курносый кубУсечённый кубИкосододекаэдр
- 13. Каталановы или двойственные тела
- 14. Ромбододекаэдр, — многогранник, составленный из двенадцати одинаковых ромбов.
- 15. Тетракисгексаэдр – это многогранник, состоящий из 24
- 16. Пентакисдодекаэдр
- 17. Пентагональный икоситетраэдрРазнообразие Каталановых телТриакисоктаэдрДельтоидальный гексеконтаэдрРомботриаконтаэдрДельтоидальный икоситетраэдр
- 18. Звёзчатые многогранникиЗвёздчатый многогранник (звёздчатое тело) — это
- 19. Звёздчатый октаэдрСуществует только одна звёздчатая форма октаэдра.
- 20. Додекаэдр имеет 3 звёздчатые формы: малый звёздчатый
- 21. Икосаэдр имеет 59 звёздчатых форм. Одна из
- 22. Звездчатые многогранники очень декоративны, что позволяет широко
Слайд 2Определение: выпуклый многогранник называется правильным, если все его грани равные правильные
Существует всего 5 видов правильных многогранников:
Тетраэдр
Гексаэдр (Куб)
Октаэдр
Икосаэдр
Додекаэдр
Платоновы тела
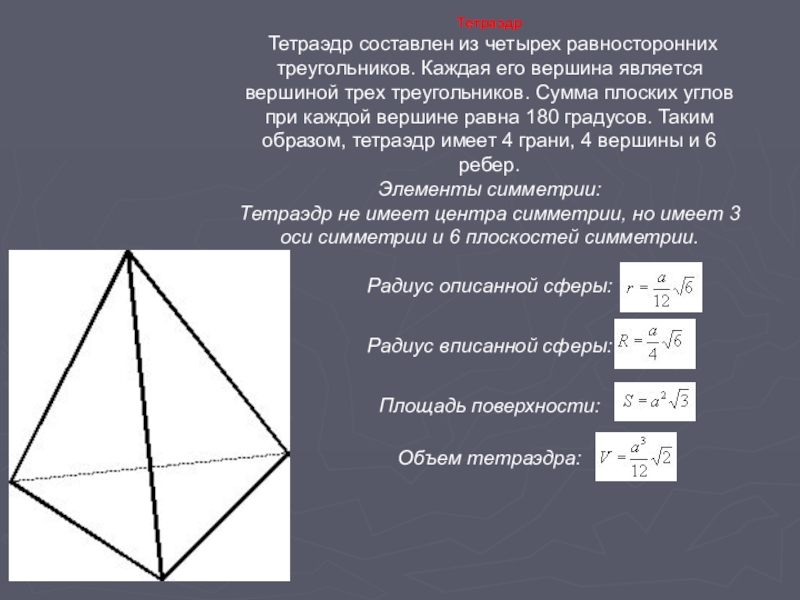
Слайд 3Тетраэдр
Тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является
Элементы симметрии:
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем тетраэдра:
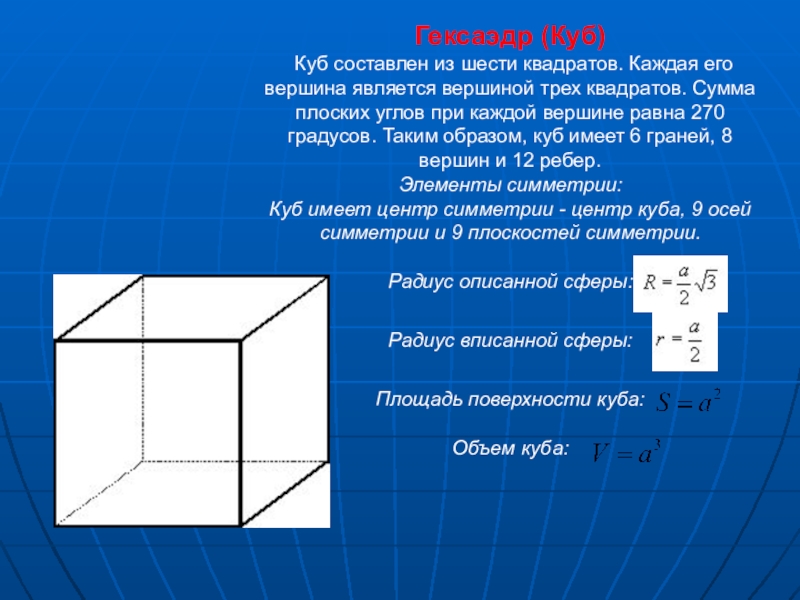
Слайд 4Гексаэдр (Куб)
Куб составлен из шести квадратов. Каждая его вершина является
Элементы симметрии:
Куб имеет центр симметрии - центр куба, 9 осей симметрии и 9 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности куба:
Объем куба:
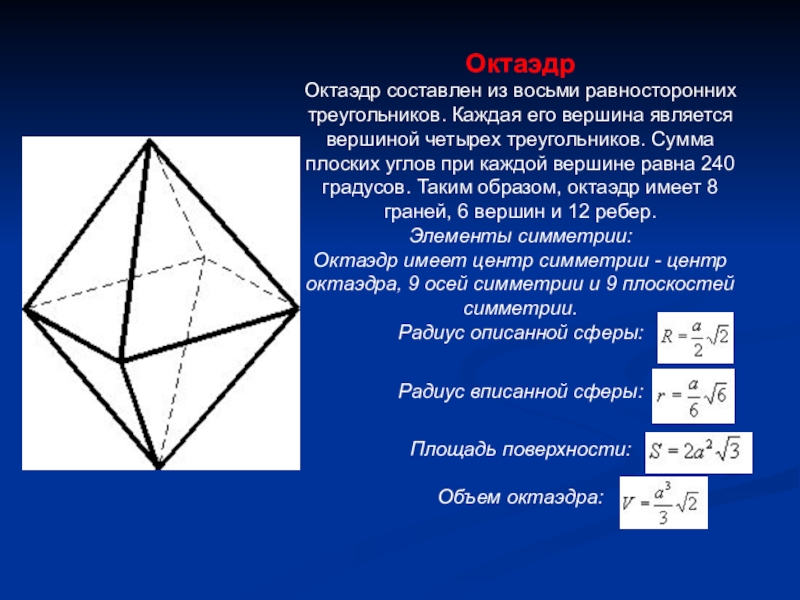
Слайд 5Октаэдр
Октаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является
Элементы симметрии:
Октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем октаэдра:
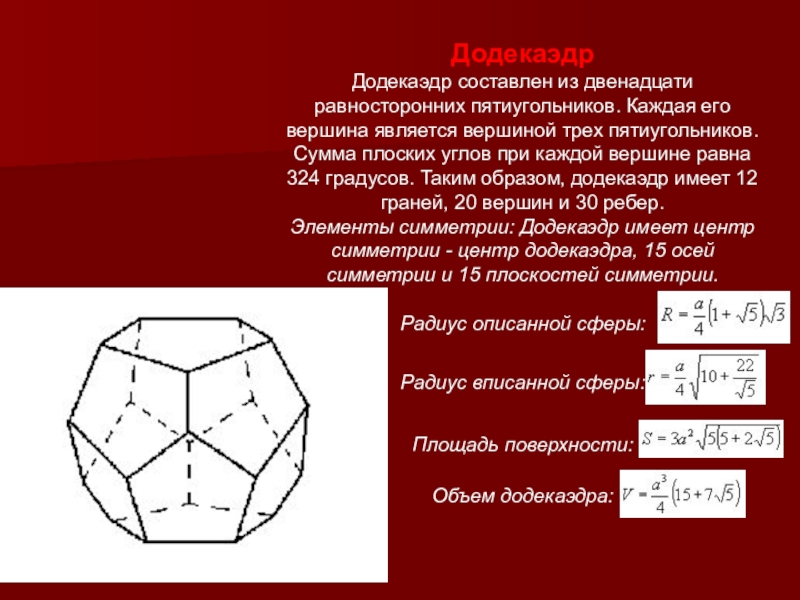
Слайд 6Додекаэдр
Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его вершина является вершиной
Элементы симметрии: Додекаэдр имеет центр симметрии - центр додекаэдра, 15 осей симметрии и 15 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем додекаэдра:
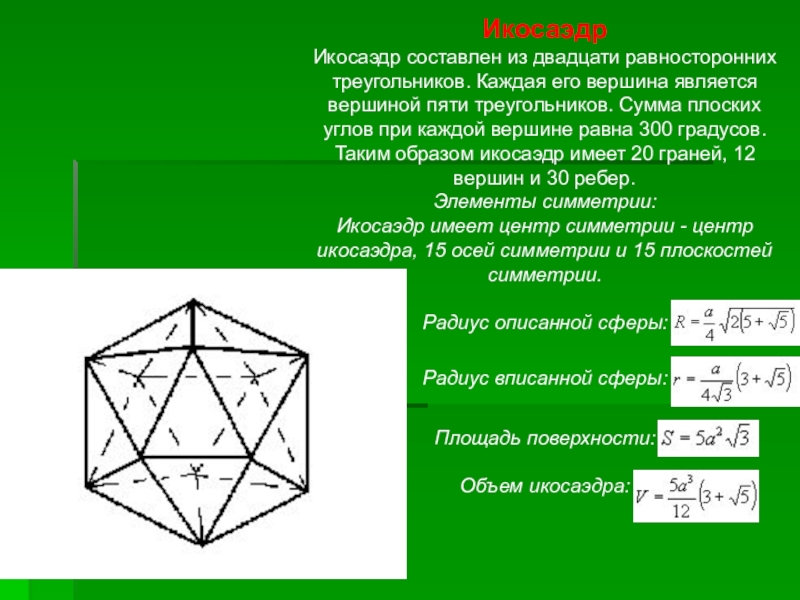
Слайд 7Икосаэдр
Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной
Элементы симметрии:
Икосаэдр имеет центр симметрии - центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем икосаэдра:
Слайд 8Кроме правильных, существует тринадцать многогранников, которые впервые открыл и описал Архимед
Все многогранные углы у них равны, а грани – правильные многоугольники разных видов. Причем в каждой вершине сходится одно и тоже количество граней.
Тела Архимеда
«Архимедовы тела» можно получить с помощью операции «усечения», состоящей в отсечении плоскостями углов многогранника.
Слайд 9Ромбокубооктаэдр.
Его поверхность состоит из граней куба и октаэдра, к которым
В форме ромбокубооктаэдра построено национальная библиотека Беларуси.
Ромбокубооктаэдр
Слайд 10Кубооктаэдр — полуправильный многогранник, состоящий из 14 граней (8 правильных треугольников и
Кубооктаэдр
объём:
площадь:
двугранный угол:
Слайд 11Ромбоикосододекаэдр —полуправильный многогранник, состоящий из 12 правильных ятиугольников, 30 квадратов и 20
Он состоит из:
62 граней
120 рёбер
60 вершин
При каждой вершине находятся четыре грани (2 квадрата, треугольник и пятиугольник)
Ромбоикосододекаэдр
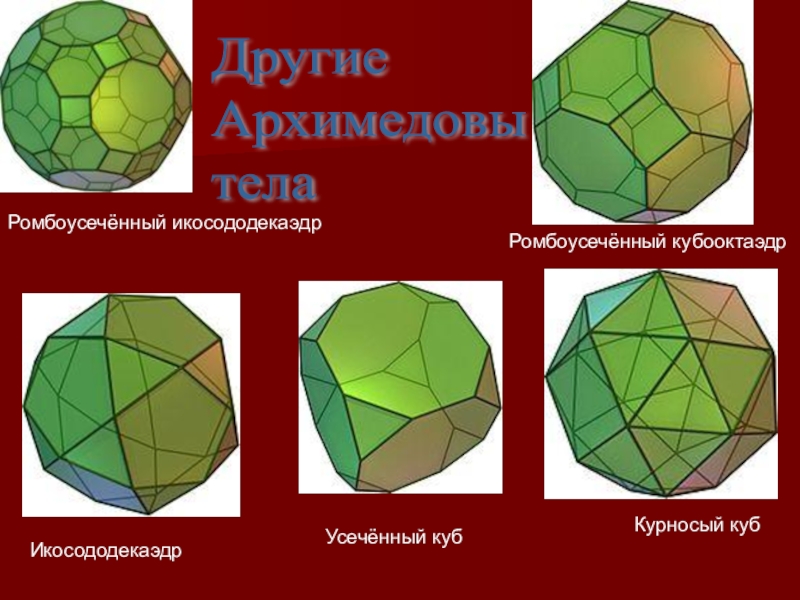
Слайд 12Другие
Архимедовы
тела
Ромбоусечённый икосододекаэдр
Ромбоусечённый кубооктаэдр
Курносый куб
Усечённый куб
Икосододекаэдр
Слайд 14Ромбододекаэдр, — многогранник, составленный из двенадцати одинаковых ромбов. У ромбостороннего додекаэдра 14
Ромбододекаэдр
Слайд 15Тетракисгексаэдр – это многогранник, состоящий из 24 треугольников. По сути, это
У этого многогранника:
24 грани
14 вершин
36 рёбер
Каждый двугранный угол тетракисгексаэдра приблизительно равен
В природе форму тетракисгексаэдр могут принимать кристаллы меди и флюорита.
Тетракисгексаэдр
Слайд 17
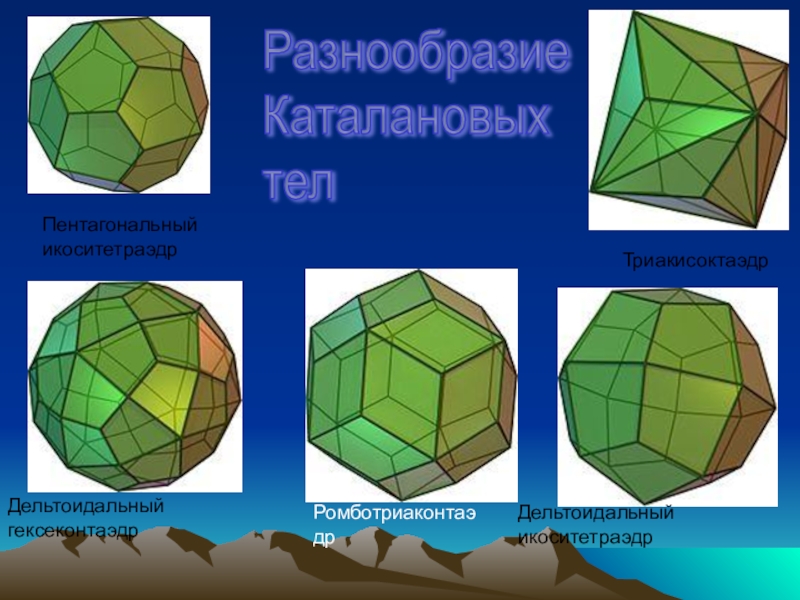
Пентагональный икоситетраэдр
Разнообразие
Каталановых
тел
Триакисоктаэдр
Дельтоидальный гексеконтаэдр
Ромботриаконтаэдр
Дельтоидальный икоситетраэдр
Слайд 18Звёзчатые многогранники
Звёздчатый многогранник (звёздчатое тело) — это невыпуклый многогранник, грани которого
Звёздчатой формой многогранника называется многогранник, полученный путём продления граней данного многогранника через рёбра до их следующего пересечения с другими гранями по новым рёбрам.
Слайд 19Звёздчатый октаэдр
Существует только одна звёздчатая форма октаэдра. Звёздчатый октаэдр был открыт
Слайд 20Додекаэдр имеет 3 звёздчатые формы: малый звёздчатый додекаэдр, большой додекаэдр, большой
Звёздочные формы додекаэдра
Слайд 21Икосаэдр имеет 59 звёздчатых форм. Одна из этих звёздчатых форм
называемая большим
Звёздчатые формы икосаэдра
Слайд 22Звездчатые многогранники очень декоративны, что позволяет широко применять их в ювелирной
Многие формы звездчатых многогранников подсказывает сама природа. Снежинки - это звездчатые многогранники
Звёздчатые многогранники
в жизни человека