- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему: Многогранники
Содержание
- 1. Презентация по геометрии на тему: Многогранники
- 2. АРХИМЕДОВЫ ТЕЛАТЕОРИЯ
- 3. АРХИМЕДОВЫ ТЕЛА Многогранник называется равноугольно-полуправильным или архимедовым,
- 4. ПРИЗМЫ Простейшим примером архимедова многогранника может служить архимедова
- 5. АНТИПРИЗМЫ Это так называемая п-угольная архимедова антипризма.
- 6. ПРИЗМЫ И АТНИПРИЗМЫ Меняя n, мы получим две
- 7. УСЕЧЕННЫЕ МНОГОГРАННИКИ Термин "усеченный" означает, что многогранник
- 8. Усечение добавляет новые грани для каждой существующей
- 9. Может показаться, что если два архимедова
- 10. Слайд 10
- 11. Изоэдры (равногранные многогранники) В кристаллографии приходится встречаться
- 12. Изогоны (равноугольные многогранники) Обобщением понятия архимедова многогранника
- 13. Слайд 13
- 14. ПЛАТОНОВЫ ТЕЛАТЕОРИЯ
- 15. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ Выпуклый многогранник называется правильным, если
- 16. ПЛАТОНОВЫ ТЕЛА Это правильные многогранники, имеющие в
- 17. МНОГОГРАННИКИ И ТЕОЛОГИЯ Платоновы тела захватили воображение математиков,
- 18. Слайд 18
- 19. МНОГОГРАННИКИ В ПРИРОДЕКристаллы поваренной соли, тиоантимонида натрия
- 20. ТЕОРЕМА О ЧИСЛЕ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ Пусть {p, q}
- 21. где символ < означает «меньше чем». После несложных алгебраических преобразований полученное неравенство приводится к виду
- 22. Нетрудно видеть, что p и q
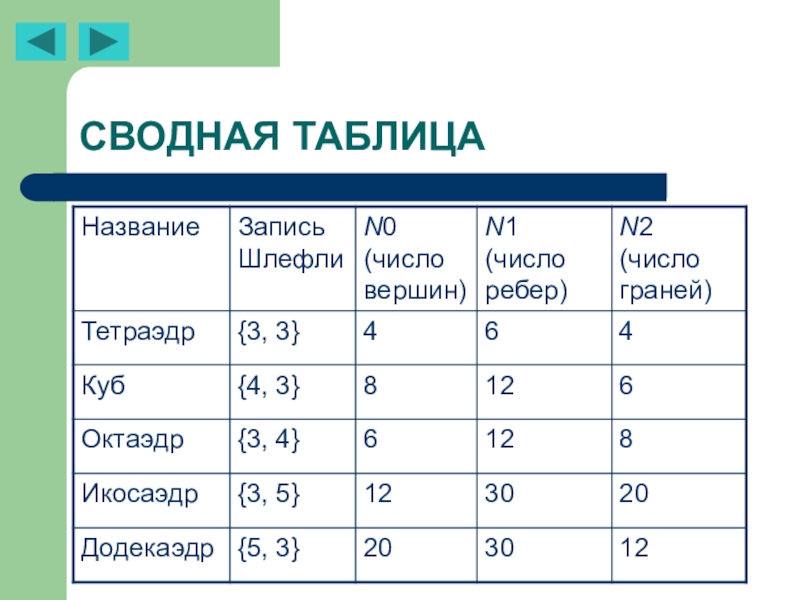
- 23. СВОДНАЯ ТАБЛИЦА
- 24. ПЛАТОНОВЫ ТЕЛАИЗОБРАЖЕНИЯ
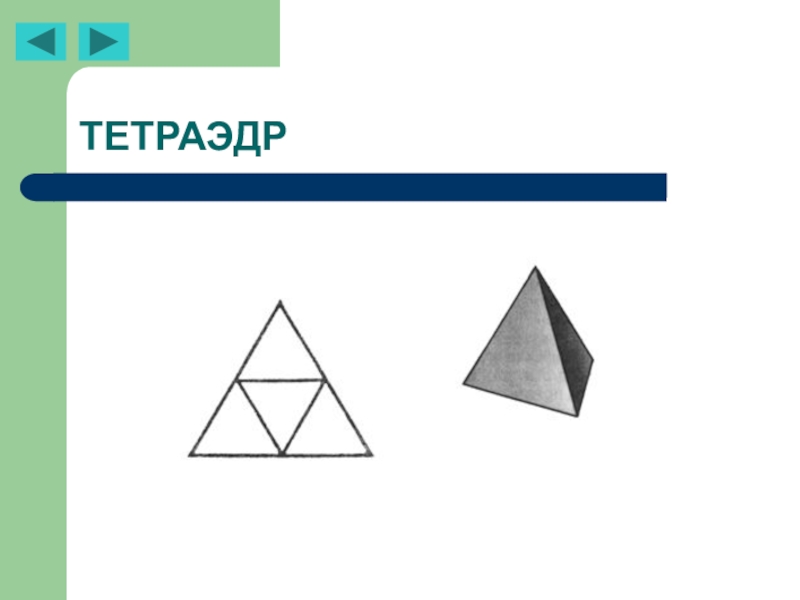
- 25. ТЕТРАЭДР
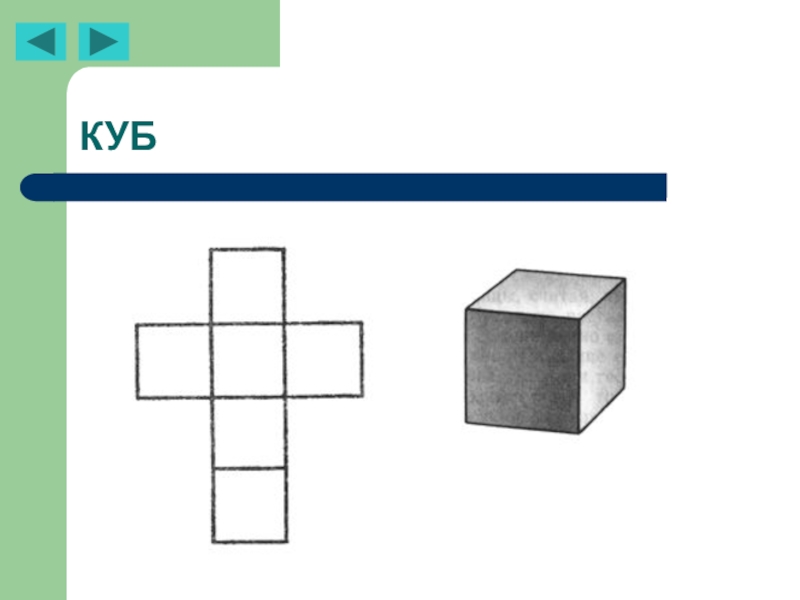
- 26. КУБ
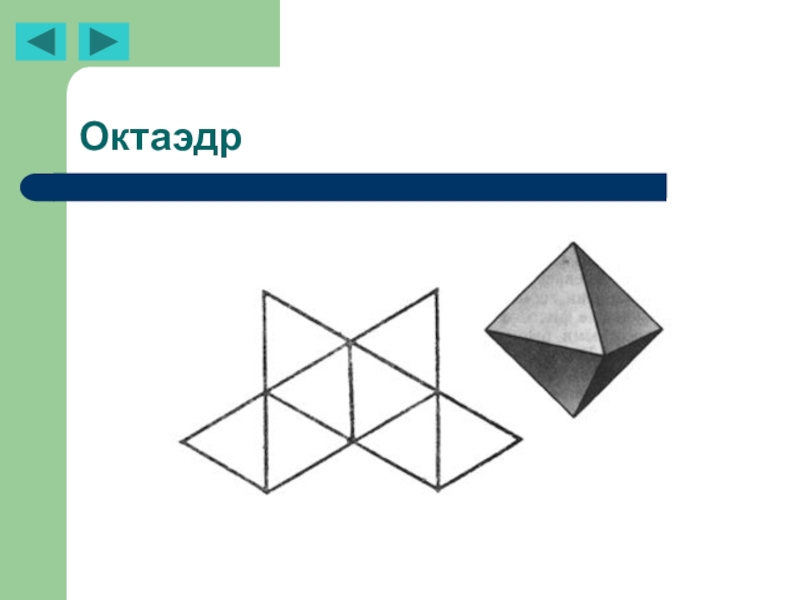
- 27. Октаэдр
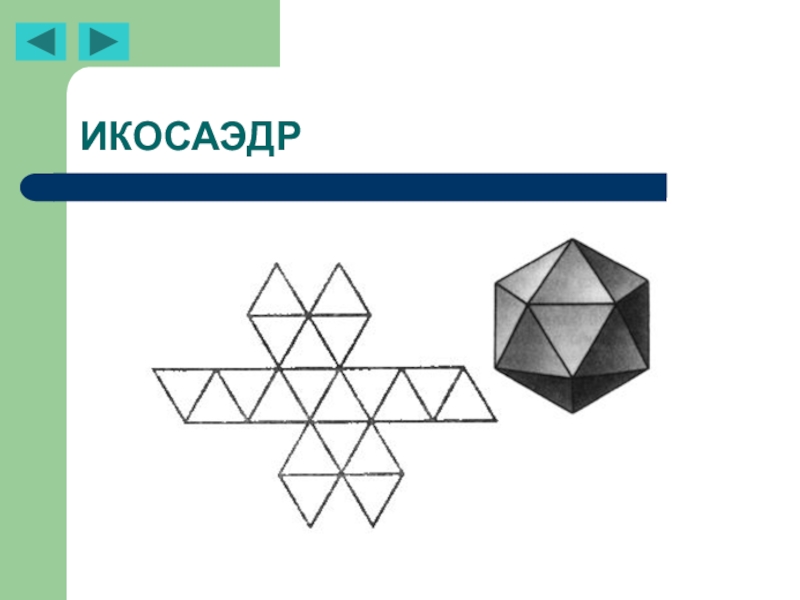
- 28. ИКОСАЭДР
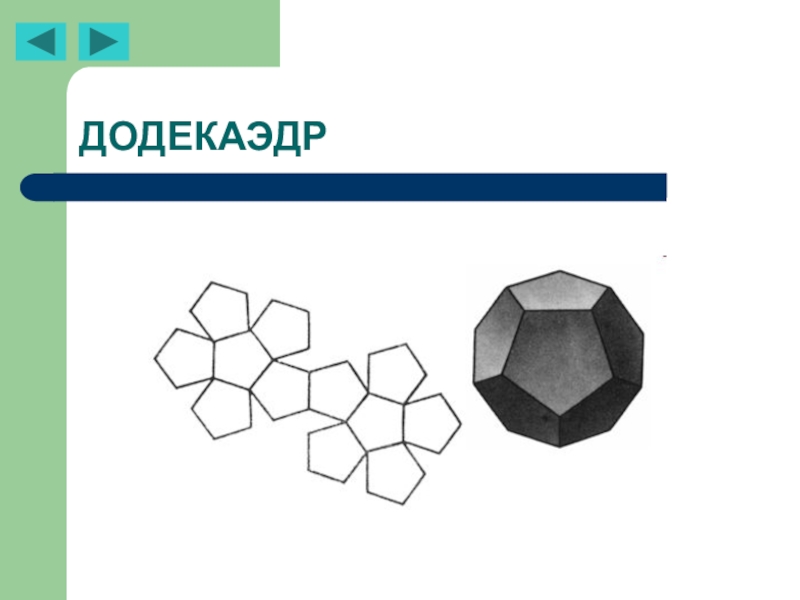
- 29. ДОДЕКАЭДР
Слайд 3АРХИМЕДОВЫ ТЕЛА
Многогранник называется равноугольно-полуправильным или архимедовым, если все его многогранные
Эти многогранники были впервые рассмотрены Архимедом в 111 в. до н. э. в недошедшем до нас сочинении, его работа дошла до нас только через сочинения других авторов. Все эти многогранники были вновь открыты и описаны в эпоху Ренессанса. Известный немецкий астроном и математик Иоганн Кеплер (1571 — 1630) в книге «Гармония мира» в 1619 г. полностью восстановил потерянную информацию о них.
Слайд 4ПРИЗМЫ
Простейшим примером архимедова многогранника может служить архимедова призма, т. е. правильная
Слайд 5АНТИПРИЗМЫ
Это так называемая п-угольная архимедова антипризма. Она может быть получена,
Слайд 6ПРИЗМЫ И АТНИПРИЗМЫ
Меняя n, мы получим две бесконечные серии архимедовых многогранников
Будем относить к одному и тому же типу два полуправильных многогранника нулевого рода, если:
при любом n у них одно и то же число n-угольных граней. (Одинаковое число треугольников, четырехугольников и т. д.);
при любом s у них одно и то же число s-гранных углов (одинаковое число трехгранных углов, одинаковое число четырехгранных углов и т. п.).
У таких многогранников также совпадают характеристики Г (количество граней), В (количество вершин), Р (количество ребер). Как показал Иоганн Кеплер, существуют (кроме рассмотренных выше серий призм и антипризм) еще 13 различных типов простых архимедовых многогранников
Слайд 7УСЕЧЕННЫЕ МНОГОГРАННИКИ
Термин "усеченный" означает, что многогранник был получен в процессе
Слайд 8Усечение добавляет новые грани для каждой существующей вершины и превращает существующие
Слайд 9
Может показаться, что если два архимедова многогранника принадлежат к одному
Слайд 11Изоэдры (равногранные многогранники)
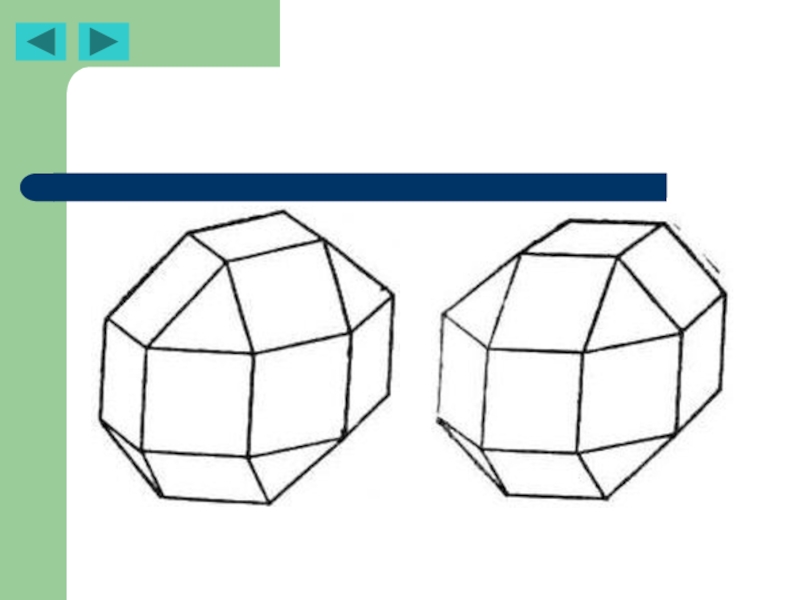
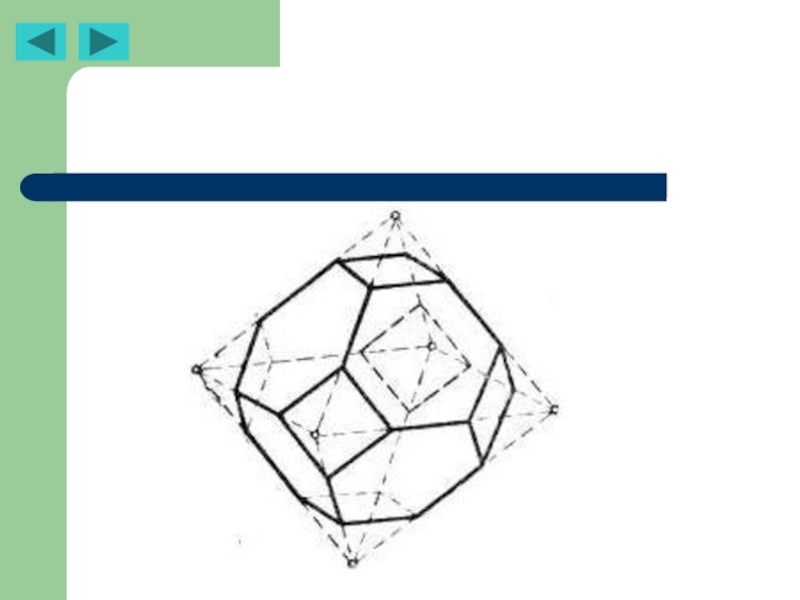
В кристаллографии приходится встречаться с классом многогранников, более
Форму изоэдра имеет, например, кристалл куприта (Сu20); это выпуклый многогранник, ограниченный 24 равными неправильными пятиугольниками.
Слайд 12Изогоны (равноугольные многогранники)
Обобщением понятия архимедова многогранника является понятие равноугольного многогранника,
Слайд 15ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Выпуклый многогранник называется правильным, если он удовлетворяет следующим двум
Все его грани – конгруэнтные правильные многоугольники;
К каждой вершине примыкает одно и то же число граней.
Если все грани – правильные р-угольники и q из них примыкают к каждой вершине, то такой правильный многогранник обозначается {p, q}. Это обозначение было предложено Л.Шлефли (1814–1895), швейцарским математиком, которому принадлежит немало изящных результатов в геометрии и математическом анализе.
Существуют также невыпуклые многогранники, у которых грани пересекаются и которые называются «правильными звездчатыми многогранниками».
Слайд 16ПЛАТОНОВЫ ТЕЛА
Это правильные многогранники, имеющие в качестве граней конгруэнтные правильные
Слайд 17МНОГОГРАННИКИ И ТЕОЛОГИЯ
Платоновы тела захватили воображение математиков, мистиков и философов древности
Слайд 19МНОГОГРАННИКИ В ПРИРОДЕ
Кристаллы поваренной соли, тиоантимонида натрия и хромовых квасцов встречаются
Слайд 20ТЕОРЕМА О ЧИСЛЕ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ
Пусть {p, q} – произвольный правильный многогранник.
Слайд 21 где символ < означает «меньше чем». После несложных алгебраических преобразований полученное
Слайд 22
Нетрудно видеть, что p и q должны быть больше 2.