- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Мир правильных многогранников(5 класс)
Содержание
- 1. Презентация по геометрии на тему Мир правильных многогранников(5 класс)
- 2. ПРАВИЛЬНЫЙ МНОГОГРАННИК-выпуклый многогранник, грани которого являются правильными
- 3. Слайд 3
- 4. Названия правильных многогранников пришли из Древней Греции,
- 5. Тетраэдр – представитель правильных выпуклых многогранников.Поверхность тетраэдра
- 6. Куб или гексаэдр – представитель правильных выпуклых
- 7. Октаэдр – представитель семейства правильных выпуклых многогранников.Октаэдр
- 8. Додекаэдр – представительсемейства правильных выпуклых многогранников.Додекаэдр имеет
- 9. Икосаэдр – представитель семейства правильных выпуклых многогранников.Поверхность
- 10. Правильные многогранники в философской картине мира Платона.
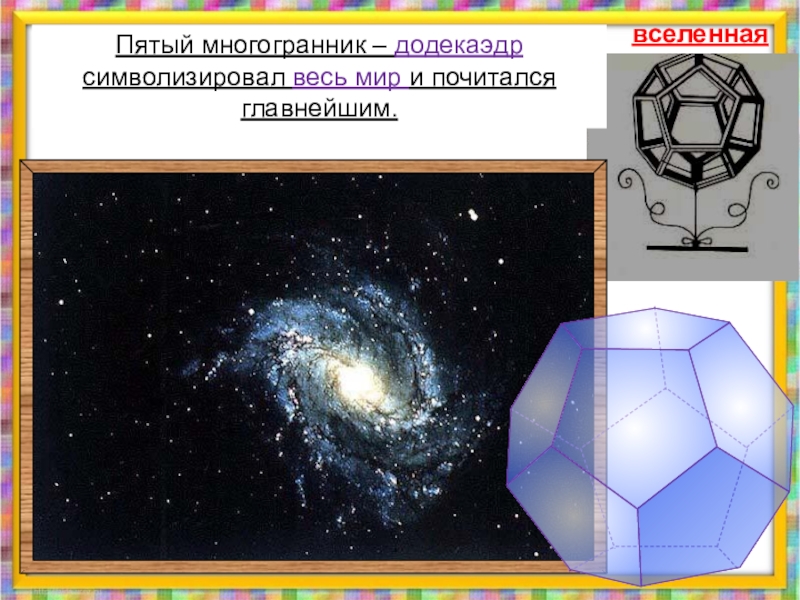
- 11. Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.
- 12. Модель Солнечнойсистемы Кеплера.
- 13. "Космический кубок" И.Кеплера
- 14. Икосаидро-додекаидроваяструктура Земли.
- 15. Слайд 15
- 16. Слайд 16
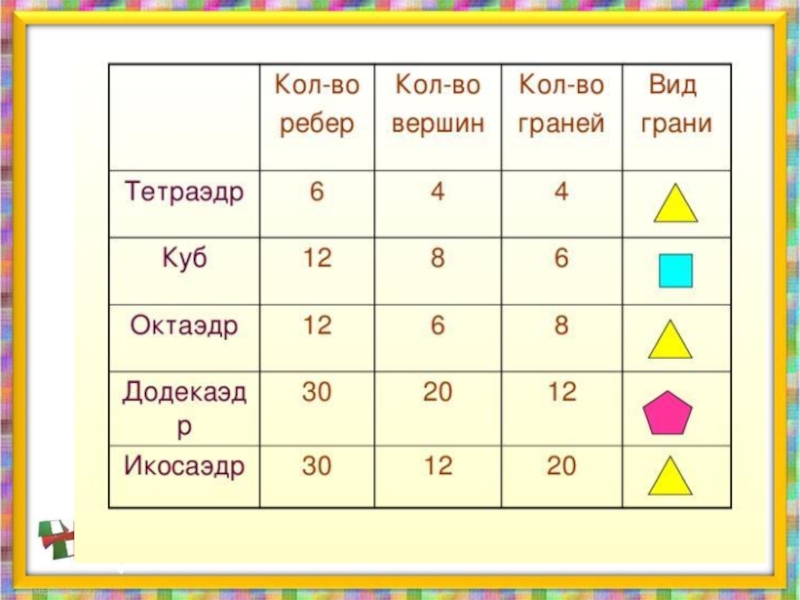
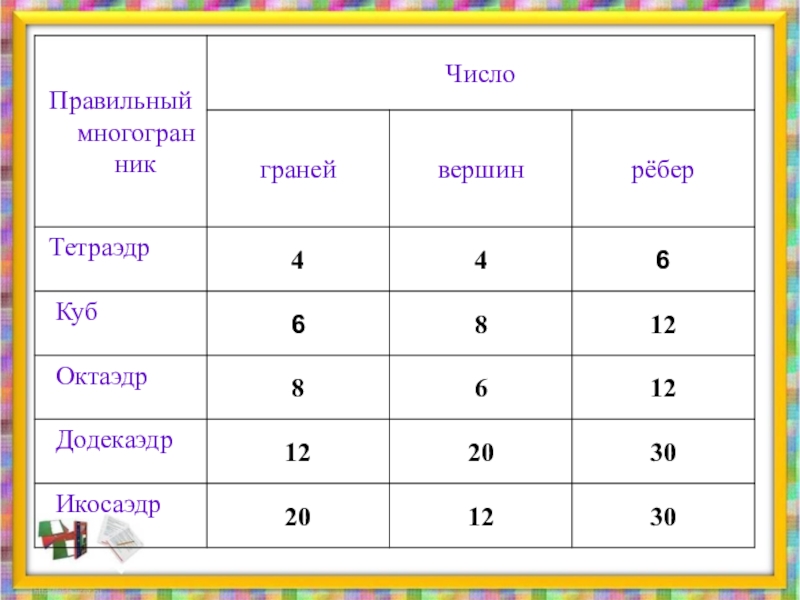
- 17. Теорема Эйлера Число вершин плюс
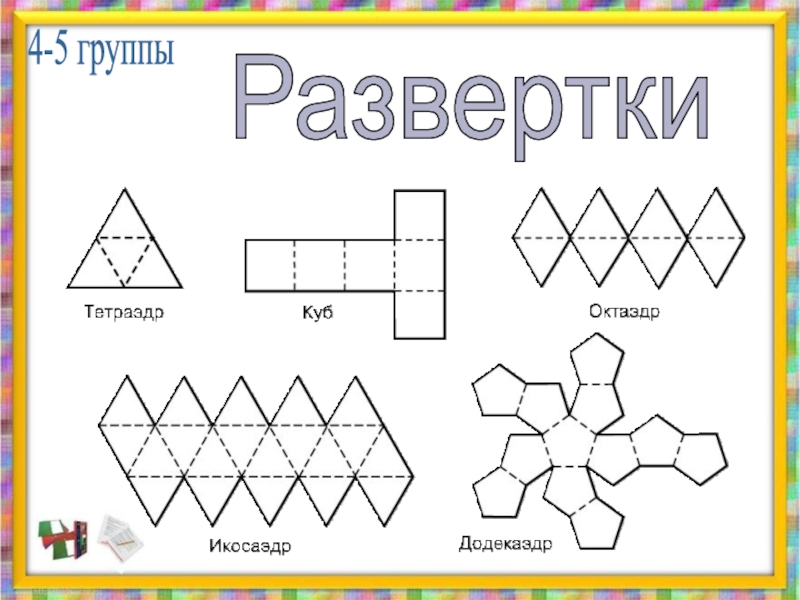
- 18. 4-5 группыРазвертки
- 19. Тетраэдр.Эта фигура состоит из четырех правильных треугольников.
- 20. Октаэдр.Собственно говоря, октаэдр является «двойником» куба: если
- 21. Икосаэдр.Если соединить центры граней додека-эдра прямыми линиями,
- 22. Куб.Куб — квадрат в трех измерениях, каждая
- 23. Первым свойства правильных многогранников описал древнегреческий ученый
- 24. Архимедовыми телами называются полуправильные однородные выпуклые многогранники,
- 25. Архимедовытела
- 26. Французский математик Пуансо в 1810 году построил
- 27. Малый звездчатыйдодекаэдрБольшой звездчатыйдодекаэдрБольшой икосаэдрБольшой додекаэдр
- 28. Скелет одноклеточного организма феодарии по форме
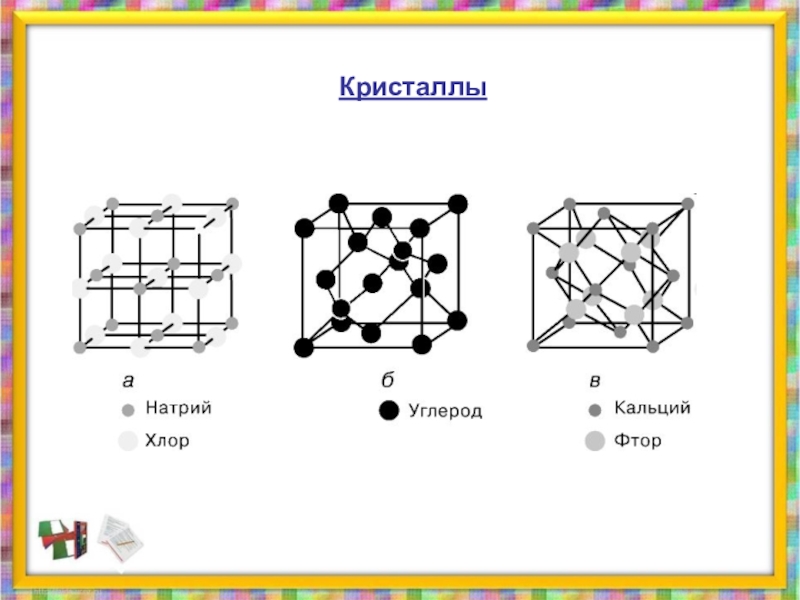
- 29. Кристаллы
- 30. Строение молекулы метана .
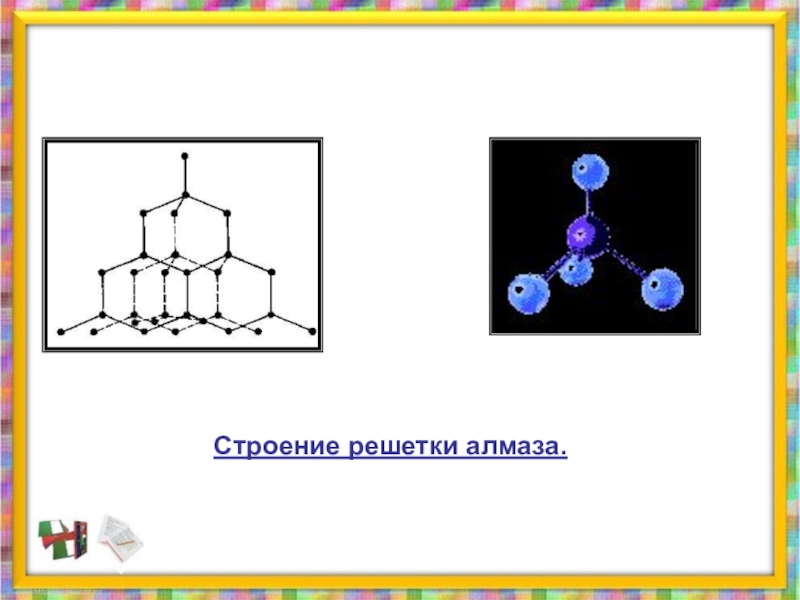
- 31. Строение решетки алмаза.
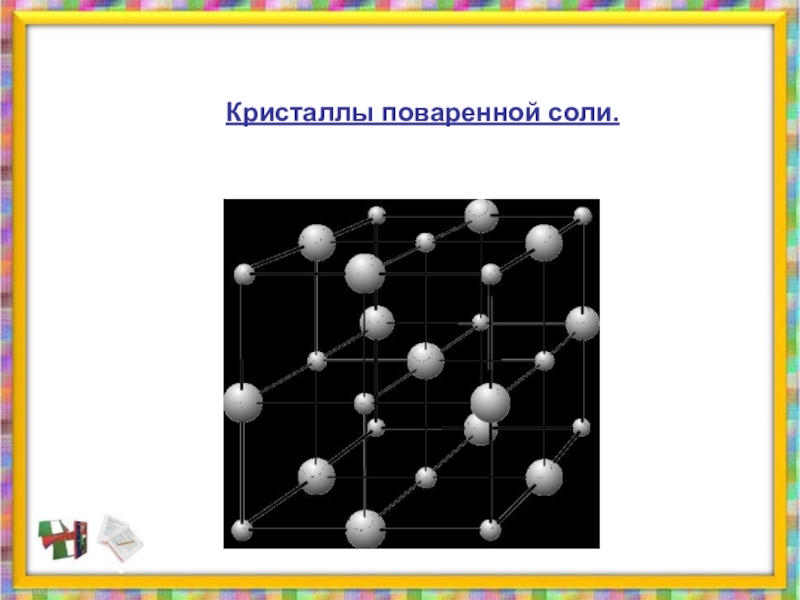
- 32. Кристаллы поваренной соли.
- 33. Вирус полиомиелита имеет форму додекаэдра.
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. Большой интерес к формам правильных многогранников проявляли
- 38. Знаменитый художник, увлекавшийся геометрией Альбрехт Дюрер (1471-
- 39. ГРАВЮРА ГОЛАНДСКОГО ХУДОЖНИКА
- 40. Слайд 40
- 41. Украшения
- 42. Правильная форма алмаза.
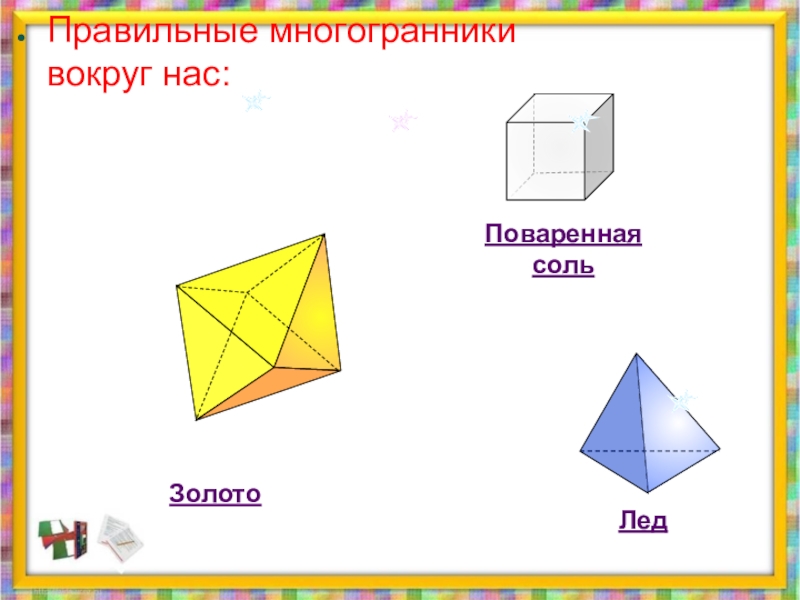
- 43. ЗолотоПравильные многогранники вокруг нас:
- 44. Памятник правильным многогранникам в городе Bagno Steinfurt в Германии
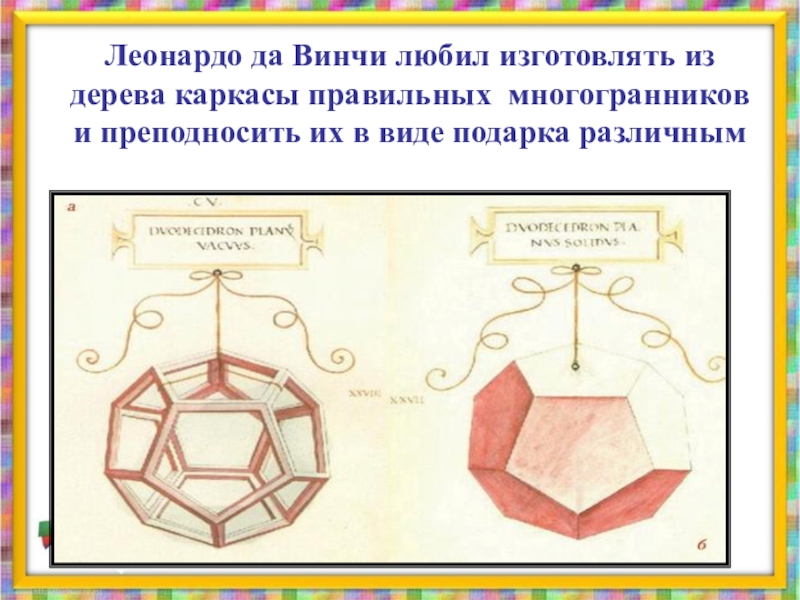
- 45. Леонардо да Винчи любил изготовлять из дерева
Слайд 2
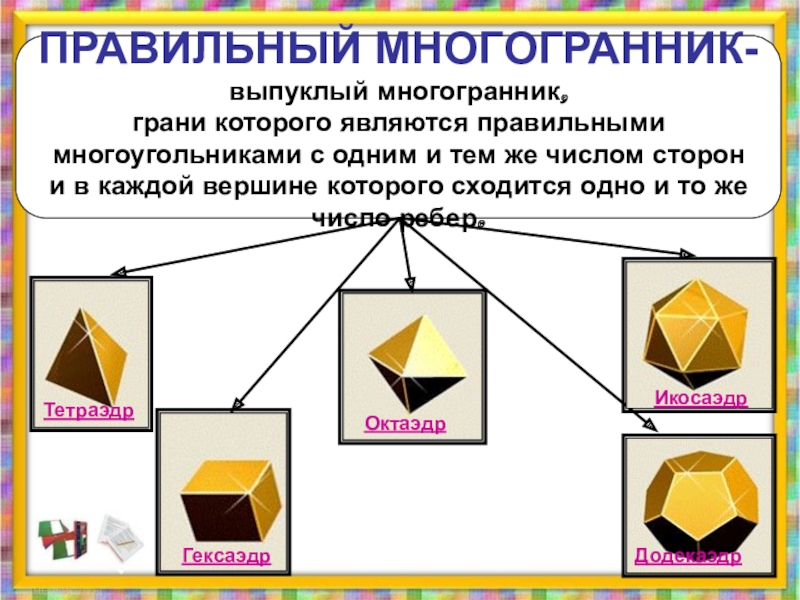
ПРАВИЛЬНЫЙ МНОГОГРАННИК-
выпуклый многогранник,
грани которого являются правильными
многоугольниками с одним и
и в каждой вершине которого сходится одно и то же число ребер.
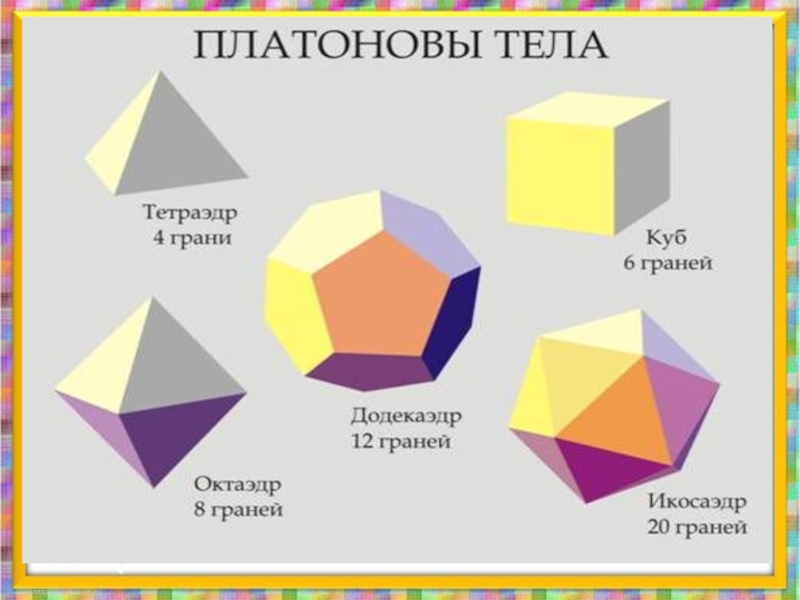
Гексаэдр
Тетраэдр
Октаэдр
Додекаэдр
Икосаэдр
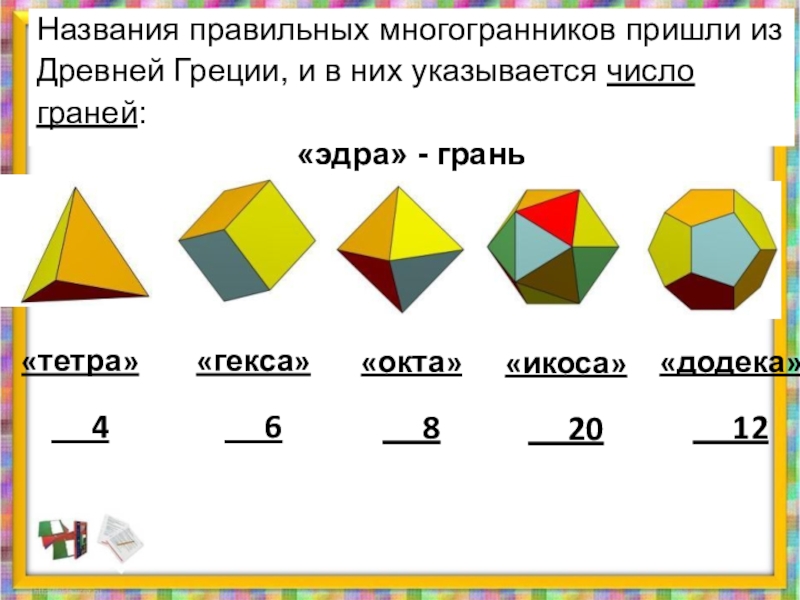
Слайд 4Названия правильных многогранников пришли из
Древней Греции, и в них указывается
граней:
«эдра» - грань
«тетра»
4
«гекса»
6
«окта»
8
«икоса»
20
«додека»
12
Слайд 5Тетраэдр – представитель правильных выпуклых многогранников.
Поверхность тетраэдра состоит из четырех равносторонних
ТЕТРАЭДР
Слайд 6Куб или гексаэдр – представитель правильных выпуклых многогранников.
Куб имеет шесть квадратных
КУБ (ГЕКСАЭДР)
Слайд 7Октаэдр – представитель семейства правильных выпуклых многогранников.
Октаэдр имеет восемь треугольных граней,
ОКТАЭДР
Слайд 8Додекаэдр – представитель
семейства правильных выпуклых многогранников.
Додекаэдр имеет двенадцать пятиугольных граней, сходящихся
ДОДЕКАЭДР
Слайд 9Икосаэдр – представитель семейства правильных выпуклых многогранников.
Поверхность икосаэдра состоит из двадцати
ИКОСАЭДР
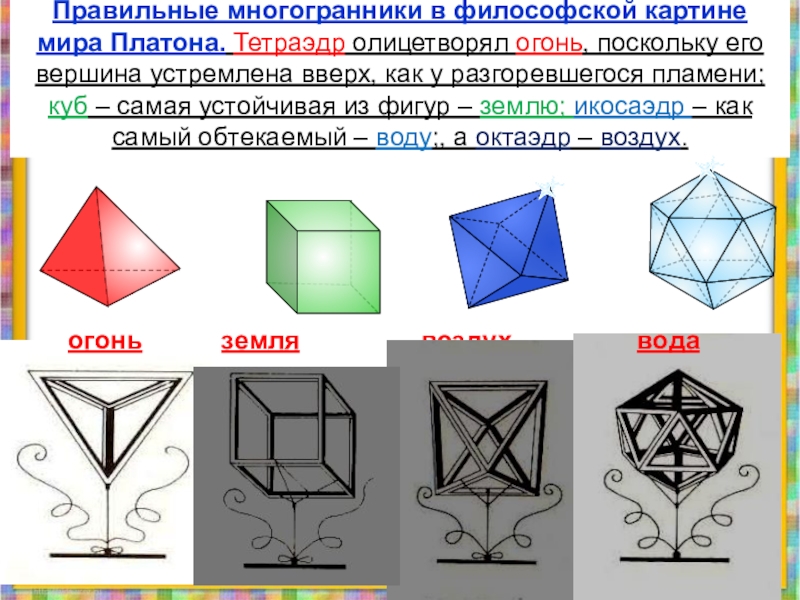
Слайд 10Правильные многогранники в философской картине мира Платона. Тетраэдр олицетворял огонь, поскольку
Слайд 19Тетраэдр.
Эта фигура состоит из четырех правильных треугольников. Если развернуть их на
Как и равносторонний треугольник, тетраэдр
представляет собой воплощение самой гармонии
и равновесия. Угловые же точки куба, как и
квадрата, находятся на разных расстояниях друг
от друга, а это значит, что в этих фигурах есть
постоянное напряжение.
Слайд 20Октаэдр.
Собственно говоря, октаэдр является «двойником» куба: если соединить
центры смежных граней куба,
Додекаэдр.
Додекаэдр — настолько сакральная форма, что во времена Пифагора, если бы кто-то произнес это слово вне пифагорейской школы, его убили бы на месте. Двумя стами годами позже, когда жил Платон, он уже мог говорить о нем, но очень осторожно. «Это отчасти объяснялось тем, что с додекаэдром связывали пятый элемент — эфир, или прану. В алхимии обычно речь идет только о четырех элементах: огне, земле, воздухе
и воде, а о пране говорится редко, потому что она считается очень сакральной. Другая причина в том, что в те времена тщательно скрывалось древнее знание, согласно которому додекаэдр близок к внешнему краю энергетического поля человека и является высшей формой сознания... Додекаэдр — это конечная точка геометрии, и он очень важен. На микроскопическом уровне додекаэдр и икосаэдр — это взаимосвязанные параметры ДНК, план - карта всей жизни»
Слайд 21Икосаэдр.
Если соединить центры граней додека-эдра прямыми линиями, то получится икосаэдр. Соединив
Слайд 22Куб.
Куб — квадрат в трех измерениях, каждая грань которого имеет те
Согласно преданию народа майя, Древо Жизни выросло из куба. Как в иудаизме, так и в исламе куб являет собой центр веры. Паломники в Мекке обходят вокруг кубического сооружения Каабы, наиболее почитаемой мусульманской святыни.
Развертка куба в пространство представляет собой крест, и если христианские церкви обычно строятся так, что имеют в плане форму креста,то это именно потому, что крест — развертка в плоскость кубического камня: церковь должна представлять собой утверждение религии Христа на земле на долгие времена.
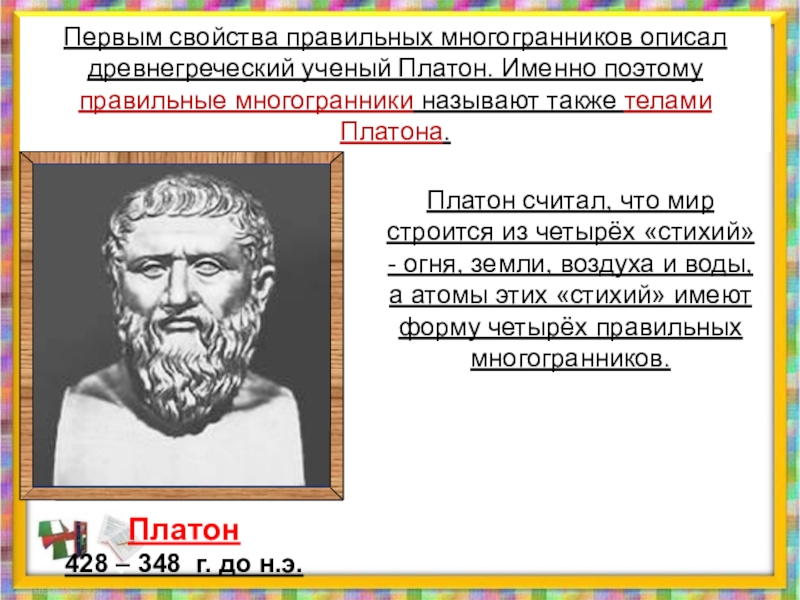
Слайд 23Первым свойства правильных многогранников описал древнегреческий ученый Платон. Именно поэтому правильные
Платон
428 – 348 г. до н.э.
Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.
Слайд 24Архимедовыми телами называются полуправильные однородные выпуклые многогранники, то есть выпуклые многогранники,
Архимедовы тела
Слайд 26
Французский математик Пуансо в 1810 году построил четыре правильных звездчатых многогранника:
Два из них знал
И. Кеплер (1571 – 1630 гг.).
В 1812 году французский математик О. Коши
доказал, что кроме пяти «платоновых тел» и
четырех «тел Пуансо» больше нет
правильных многогранников.
Слайд 28Скелет одноклеточного организма феодарии по
форме напоминает икосаэдр.
Из
Слайд 37Большой интерес к формам правильных многогранников проявляли скульпторы, архитекторы, художники.
Сальвадор
Слайд 38Знаменитый художник, увлекавшийся геометрией Альбрехт Дюрер (1471- 1528) , в известной
Слайд 45Леонардо да Винчи любил изготовлять из дерева каркасы правильных многогранников и
знаменитостям.