ТО «ЗСГК»
Хазова Е.С.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по дисциплине ЕН.03 Теория вероятности и математическая статистика на тему Элементы теории графов
Содержание
- 1. Презентация по дисциплине ЕН.03 Теория вероятности и математическая статистика на тему Элементы теории графов
- 2. Основные понятия и определенияГраф – это набор
- 3. Основные понятия и определенияЕсли из графа удалить
- 4. Основные понятия и определения
- 5. Основные понятия и определенияПростой граф называется полным,
- 6. Основные понятия и определенияСтепенью (валентностью) вершины графа
- 7. Пример 1По определению петля при вершине Vi
- 8. Основные понятия и определенияПуть – такая последовательность
- 9. Основные понятия и определенияМаршрут в графе G
- 10. Пример 2
- 11. Пример 2X1, X2, X3, X5, X1, X5
- 12. Основные понятия и определенияГраф называется связным, если
- 13. Основные понятия и определенияСвязный неориентированный ациклический граф называется деревом, а множество деревьев называется лесом.
- 14. Плоские графыУсловием того, чтобы граф был плоским получено 80 лет назад польским математиком К. Куратовским.
- 15. Теорема К. КуратовскогоДля того, чтобы граф был
- 16. Теорема К. КуратовскогоМожно доказать, что каждый плоский
- 17. Представление графов
- 18. Связные и несвязные графы
- 19. Эйлеровы графы
- 20. Эйлеровы графыПусть дан неориентированный псевдограф, цепь называется
- 21. Эйлеровы графыЭйлерова цепь существует тогда и только
- 22. Остовные деревьяОстовным деревом связного неориентированного графа (X,U,Φ)
- 23. Остовные деревьяОстовным деревом связного неориентированного графа (X,U,Φ)
- 24. Алгоритм построения остовного дерева («Жадный алгоритм»)Построение остовного
- 25. Задания для самостоятельной работы:1. Найти степени вершин данного графа. Является ли этот граф эйлеровым?
- 26. Задания для самостоятельной работы:2. С помощью жадного алгоритма найти остов минимального веса в графе.
- 27. Задания для самостоятельной работы:3. Плоский граф имеет
- 28. Задания для самостоятельной работы:5. Задан граф; требуется:
- 29. Список используемой литературы:Ахо Альфред В., Хопкрофт Джон
Основные понятия и определенияГраф – это набор точек в трехмерном пространстве, некоторые пары из которых соединены непересекающимися дугами кривых. Точки указанного набора называются вершинами графа, а соединяющие их дуги – ребрами. Одна из вершин графа считается
Слайд 1Элементы теории графов
Основные понятия и определения
Плоские графы
Представление графов
Эйлеровы графы
Остовные деревья
Преподаватель ГАПОУ
Слайд 2Основные понятия и определения
Граф – это набор точек в трехмерном пространстве,
некоторые пары из которых соединены непересекающимися дугами кривых.
Точки указанного набора называются вершинами графа, а соединяющие их дуги – ребрами.
Одна из вершин графа считается начальной, другая – конечной. Тем самым на ребре устанавливается направление, которое на чертеже указывается стрелкой.
Для обозначения вершин графа используют символы v1, v2, …, vn , а для обозначения ребер или дуг – e1, e2, …, em.
Точки указанного набора называются вершинами графа, а соединяющие их дуги – ребрами.
Одна из вершин графа считается начальной, другая – конечной. Тем самым на ребре устанавливается направление, которое на чертеже указывается стрелкой.
Для обозначения вершин графа используют символы v1, v2, …, vn , а для обозначения ребер или дуг – e1, e2, …, em.
Слайд 3Основные понятия и определения
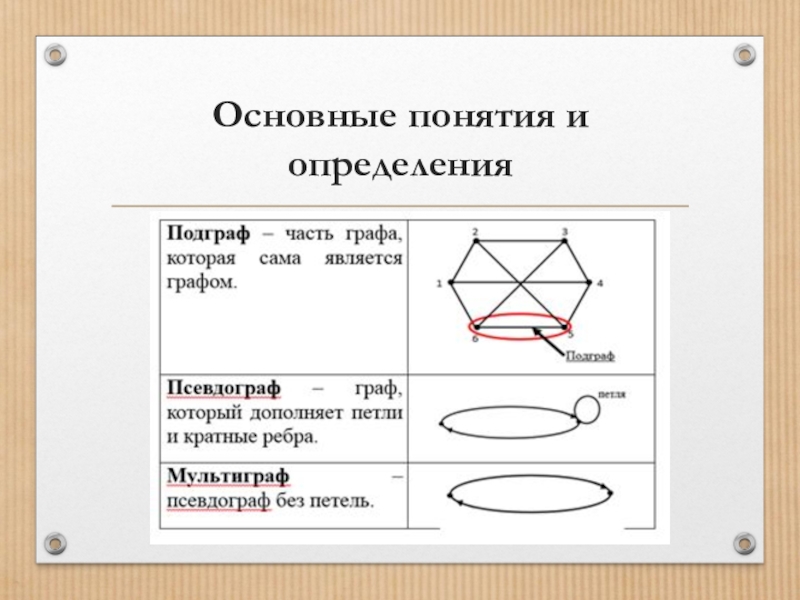
Если из графа удалить часть ребер (дуг), то
получим частичный граф.
Граф, содержащий только ребра, называется неориентированным графом.
Граф называется ориентированным (оргграф), если каждое его ребро ориентированно.
Неориентированный граф называется простым, если он не имеет петель и любые две вершины, соединенные не более, чем одним ребром.
Граф, содержащий только ребра, называется неориентированным графом.
Граф называется ориентированным (оргграф), если каждое его ребро ориентированно.
Неориентированный граф называется простым, если он не имеет петель и любые две вершины, соединенные не более, чем одним ребром.
Слайд 5Основные понятия и определения
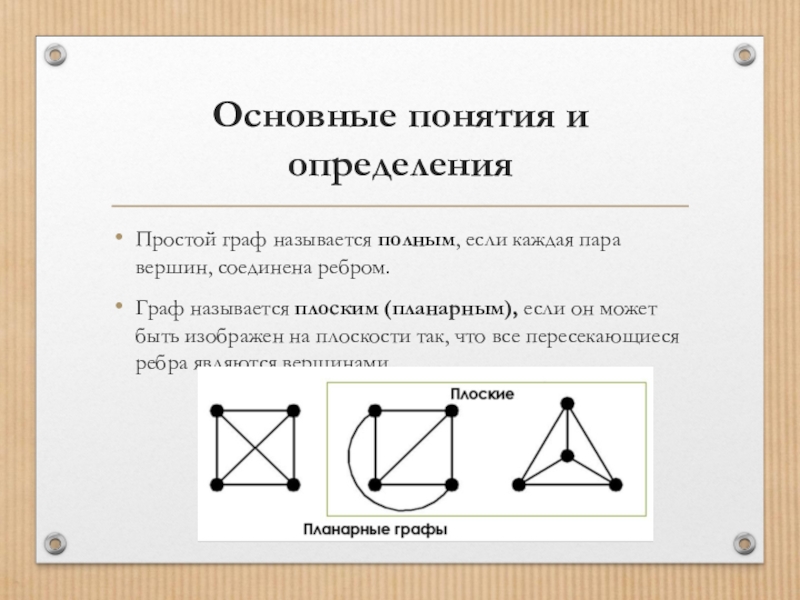
Простой граф называется полным, если каждая пара вершин,
соединена ребром.
Граф называется плоским (планарным), если он может быть изображен на плоскости так, что все пересекающиеся ребра являются вершинами.
Граф называется плоским (планарным), если он может быть изображен на плоскости так, что все пересекающиеся ребра являются вершинами.
Слайд 6Основные понятия и определения
Степенью (валентностью) вершины графа называется число ребер, проходящих
через эту вершину.
Вершина степени 1 называется висячей или концевой.
Ребро, инцидентное висячей вершине, называется висячим.
Вершина степени 0 называется изолированной.
Вершина степени 1 называется висячей или концевой.
Ребро, инцидентное висячей вершине, называется висячим.
Вершина степени 0 называется изолированной.
Слайд 7Пример 1
По определению петля при вершине Vi добавляет 2 в степень
соответствующей вершины.
В графе G на рисунке: d1 = 3, d2 = 2, d3 = 0, d4 = 1, d5 = 3, d6 =1.
V3 – изолированная вершина, V4 и V6 – висячие вершины, а е2 – висячее ребро. Сумма степеней вершин равна 10. Число ребер равно 5.
В графе G на рисунке: d1 = 3, d2 = 2, d3 = 0, d4 = 1, d5 = 3, d6 =1.
V3 – изолированная вершина, V4 и V6 – висячие вершины, а е2 – висячее ребро. Сумма степеней вершин равна 10. Число ребер равно 5.
Слайд 8Основные понятия и определения
Путь – такая последовательность дуг (в ориентированном графе),
в которой конец одной дуги является началом другой дуги.
Простой путь – путь, в котором ни одна дуга не встречается дважды.
Элементарный путь – путь, в котором ни одна вершина не встречается дважды.
Контур – путь, у которого конечная вершина совпадает с начальной вершиной.
Длина пути (контура) – число дуг пути (или сумма длин его дуг, если длины дуг заданы).
Простой путь – путь, в котором ни одна дуга не встречается дважды.
Элементарный путь – путь, в котором ни одна вершина не встречается дважды.
Контур – путь, у которого конечная вершина совпадает с начальной вершиной.
Длина пути (контура) – число дуг пути (или сумма длин его дуг, если длины дуг заданы).
Слайд 9Основные понятия и определения
Маршрут в графе G представляет собой конечную чередующуюся
последовательность вершин и ребер.
Маршрут называется открытым, если его концевые вершины различны, в противном случае он называется замкнутым.
Маршрут называется открытым, если его концевые вершины различны, в противном случае он называется замкнутым.
Слайд 11Пример 2
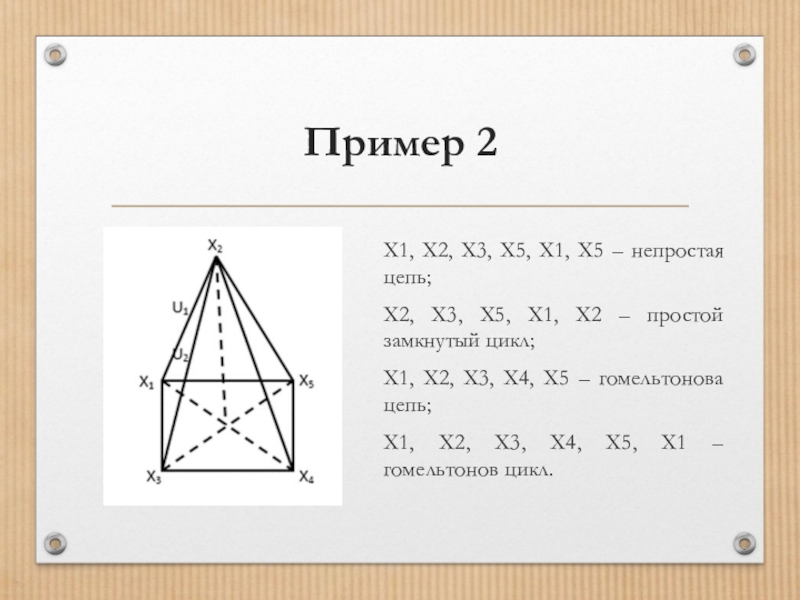
X1, X2, X3, X5, X1, X5 – непростая цепь;
X2, X3,
X5, X1, X2 – простой замкнутый цикл;
X1, X2, X3, X4, X5 – гомельтонова цепь;
X1, X2, X3, X4, X5, X1 – гомельтонов цикл.
X1, X2, X3, X4, X5 – гомельтонова цепь;
X1, X2, X3, X4, X5, X1 – гомельтонов цикл.
Слайд 12Основные понятия и определения
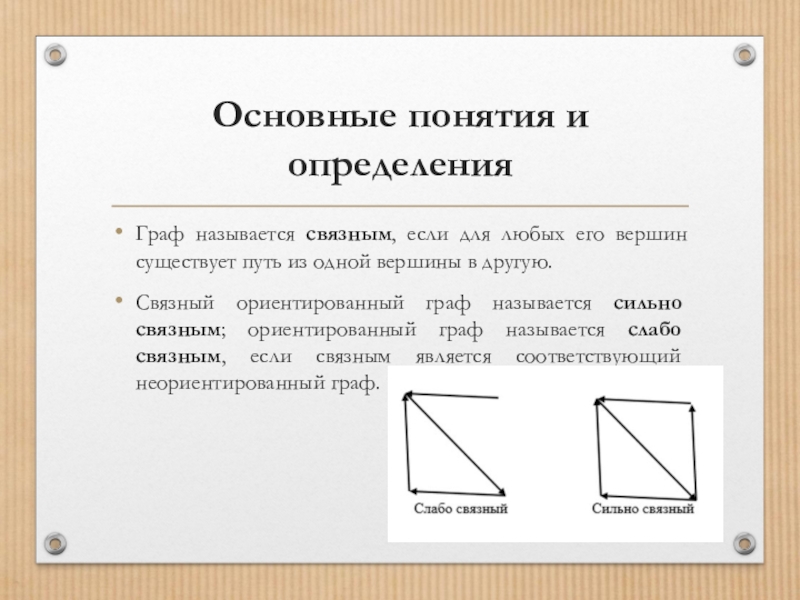
Граф называется связным, если для любых его вершин
существует путь из одной вершины в другую.
Связный ориентированный граф называется сильно связным; ориентированный граф называется слабо связным, если связным является соответствующий неориентированный граф.
Связный ориентированный граф называется сильно связным; ориентированный граф называется слабо связным, если связным является соответствующий неориентированный граф.
Слайд 13Основные понятия и определения
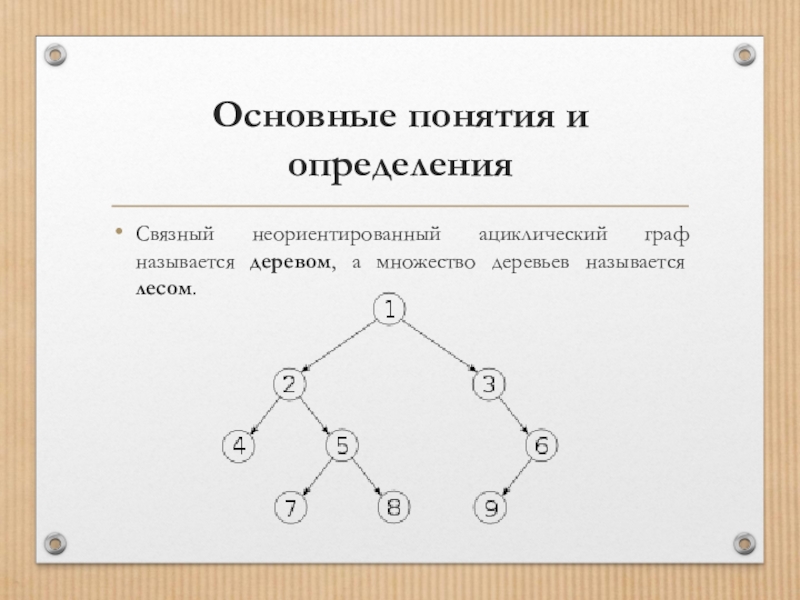
Связный неориентированный ациклический граф называется деревом, а множество
деревьев называется лесом.
Слайд 14Плоские графы
Условием того, чтобы граф был плоским получено 80 лет назад
польским математиком К. Куратовским.
Слайд 15Теорема К. Куратовского
Для того, чтобы граф был плоским необходимо и достаточно,
чтобы он не содержал внутри себя никакого подграфа, который можно было бы сжать до 5 или 6 участка.
Слайд 16Теорема К. Куратовского
Можно доказать, что каждый плоский граф можно начертить на
плоскости так, что все его ребра будут изображены прямолинейными отрезками при условии, что никакая пара его вершин не соединена более чем одним ребром.
Изоморфны
В-Р+Г=5-8+5=1
В-Р+Г=5-8+5=1
Для любого плоского графа:
В-Р+Г.
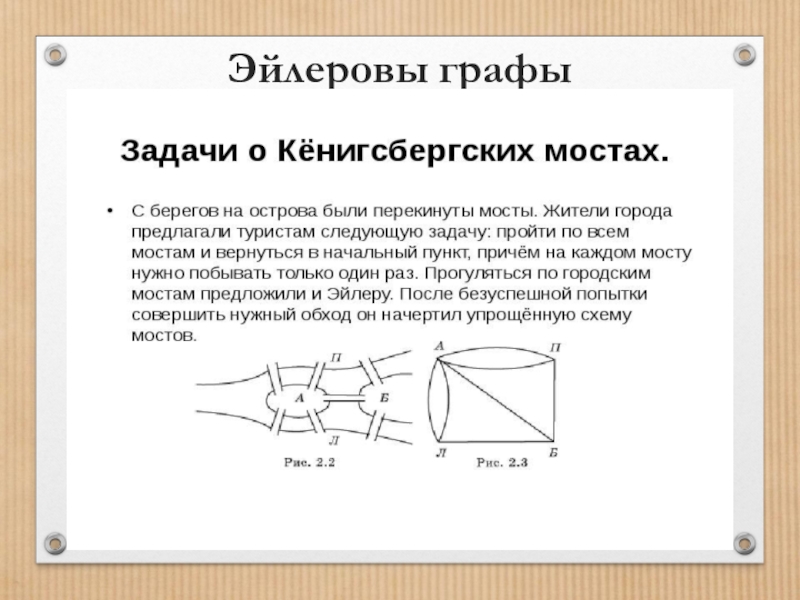
Слайд 20Эйлеровы графы
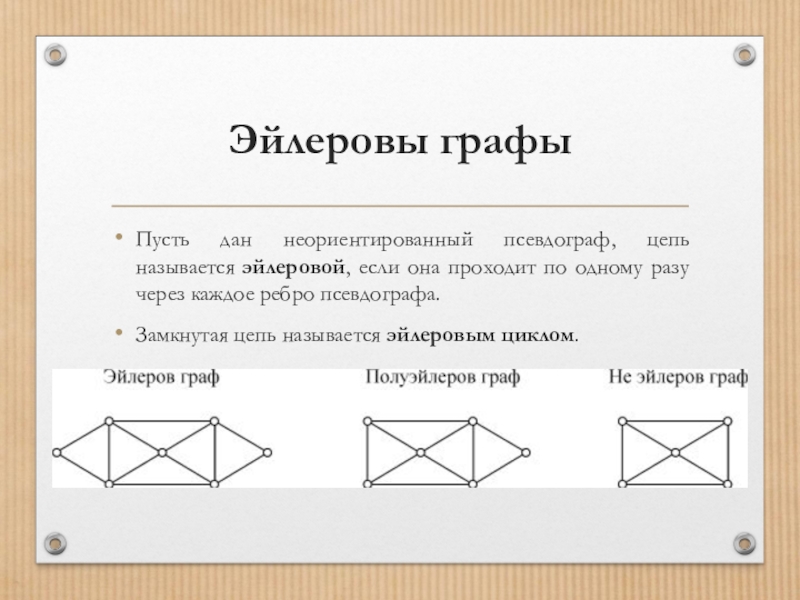
Пусть дан неориентированный псевдограф, цепь называется эйлеровой, если она проходит
по одному разу через каждое ребро псевдографа.
Замкнутая цепь называется эйлеровым циклом.
Замкнутая цепь называется эйлеровым циклом.
Слайд 21Эйлеровы графы
Эйлерова цепь существует тогда и только тогда, когда выполняются следующие
условия:
Граф связный.
Степени внутри вершин четные.
Если A – начало пути, а B – конец пути и A не совпадает с B, то их степени нечетные.
Если A – начало пути, а B – конец пути и A совпадает с B, то их степени четные.
Граф связный.
Степени внутри вершин четные.
Если A – начало пути, а B – конец пути и A не совпадает с B, то их степени нечетные.
Если A – начало пути, а B – конец пути и A совпадает с B, то их степени четные.
Слайд 22Остовные деревья
Остовным деревом связного неориентированного графа (X,U,Φ) называется дерево Г0=(X,U,Φ).
Дерево –
граф не содержащий циклов.
Теорема: Всякое дерево с n-вершинами содержит (n-1) ребро.
Теорема: Всякое дерево с n-вершинами содержит (n-1) ребро.
Слайд 23Остовные деревья
Остовным деревом связного неориентированного графа (X,U,Φ) называется дерево Г0=(X,U,Φ).
Дерево –
граф не содержащий циклов.
Теорема: Всякое дерево с n-вершинами содержит (n-1) ребро.
Минимальным остовным деревом (лесом) называется остовное дерево (лес) с минимальным общим весом всех его ребер.
Теорема: Всякое дерево с n-вершинами содержит (n-1) ребро.
Минимальным остовным деревом (лесом) называется остовное дерево (лес) с минимальным общим весом всех его ребер.
Слайд 24Алгоритм построения остовного дерева («Жадный алгоритм»)
Построение остовного дерева начинается с произвольной
вершины x1.
Среди ребер, проходящих через x1, выбирается ребро x1x2 с наименьшим весом и вершина x2 включается в остовное дерево.
Среди ребер, выходящих из x1x2, ищем ребро с наименьшей длиной, допустим x, и вершину x3 включаем в оставное дерево.
Продолжаем эту процедуру, пока все вершины не будут включены в это дерево. Получим минимальное оставное дерево.
Далее необходимо доказать, что результат не зависит от выбранной первоначальной вершины.
Среди ребер, проходящих через x1, выбирается ребро x1x2 с наименьшим весом и вершина x2 включается в остовное дерево.
Среди ребер, выходящих из x1x2, ищем ребро с наименьшей длиной, допустим x, и вершину x3 включаем в оставное дерево.
Продолжаем эту процедуру, пока все вершины не будут включены в это дерево. Получим минимальное оставное дерево.
Далее необходимо доказать, что результат не зависит от выбранной первоначальной вершины.
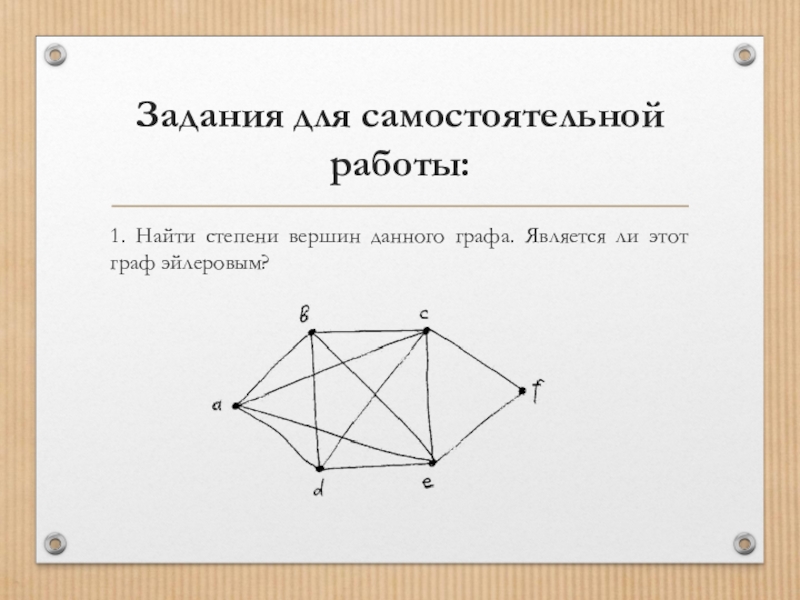
Слайд 25Задания для самостоятельной работы:
1. Найти степени вершин данного графа. Является ли
этот граф эйлеровым?
Слайд 26Задания для самостоятельной работы:
2. С помощью жадного алгоритма найти остов минимального
веса в графе.
Слайд 27Задания для самостоятельной работы:
3. Плоский граф имеет n = 8 вершин,
m =10 рёбер и f = 4 грани. Является ли он связным?
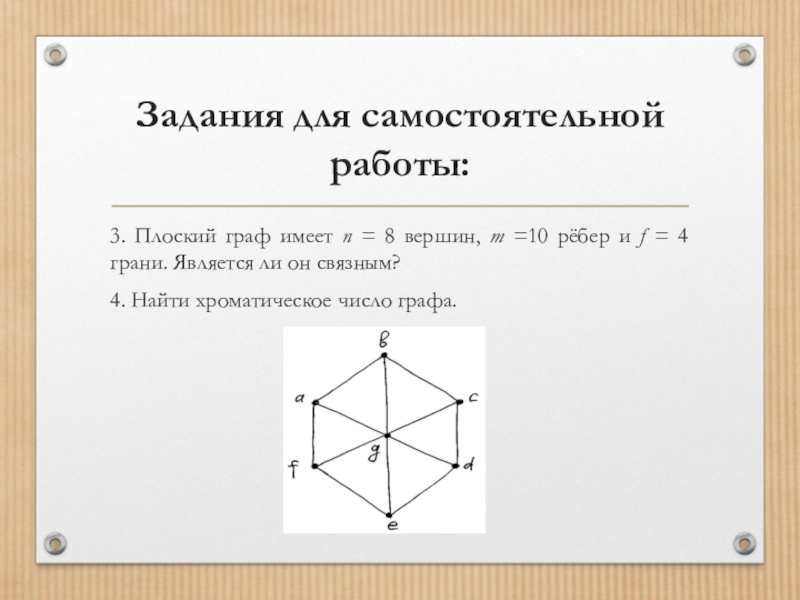
4. Найти хроматическое число графа.
4. Найти хроматическое число графа.
Слайд 28Задания для самостоятельной работы:
5. Задан граф; требуется:
записать матрицу инциденций графа;
проверить
выполнение необходимого условия планарности графа; найти число граней графа;
выполнить чертёж графа, доказывающий его планарность; показать на чертеже все грани графа
выполнить чертёж графа, доказывающий его планарность; показать на чертеже все грани графа
Слайд 29Список используемой литературы:
Ахо Альфред В., Хопкрофт Джон Э. Структуры данных и
алгоритмы. – М.: Вильямс, 2000. – 384 с.
Левитин, А. Алгоритмы: введение в разработку и анализ. – М.: Вильямс, 2006. – 576 с.
Спирина, М.С., Спирин, П.А. Дискретная математика. – М.: Академия, 2004. – 368 с.
Левитин, А. Алгоритмы: введение в разработку и анализ. – М.: Вильямс, 2006. – 576 с.
Спирина, М.С., Спирин, П.А. Дискретная математика. – М.: Академия, 2004. – 368 с.