- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Логарифмы. Применение логарифмов
Содержание
- 1. Презентация по алгебре на тему Логарифмы. Применение логарифмов
- 2. обобщить понятие логарифма; повторить определение
- 3. Установите соответствие
- 4. Правильный ответ
- 5. Вычислите:
- 6. ДЖОН НЕПЕР (1550-1617) Шотландский математик – изобретатель
- 7. ПАЛОЧКИ НЕПЕРА НЕПЕР ПРЕДЛОЖИЛ
- 8. ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА В 1614 году шотландский математик
- 9. Математический диктант1. 2. 3.4. 5.6.7.
- 10. Ответы: 1. 2 2. 4
- 11. Выставим оценки…11 – 12 правильных ответов -
- 12. Company Logowww.themegallery.comСферы примененияЛогарифм ПрименяетсяВ ЛитературеВ музыкеВ биологииВ астрономииВ логике
- 13. Company Logowww.themegallery.comВ музыкеИзвестный физик Эйхенвальд вспоминал: “Товарищ
- 14. Ноте «до» соответствует частота, равная n колебаниям
- 15. Логарифмируя эту формулу, получаем
- 16. Принимая частоту самого низкого «до» за единицу n=1 и приводя логарифмы к основанию 2, имеем
- 17. Company Logowww.themegallery.comВ литературеЛюбопытная задача, взятая из книги
- 18. Логарифм и ощущения! Человеческий организм способен
- 19. Логарифмическая спираль Спираль – это плоская кривая
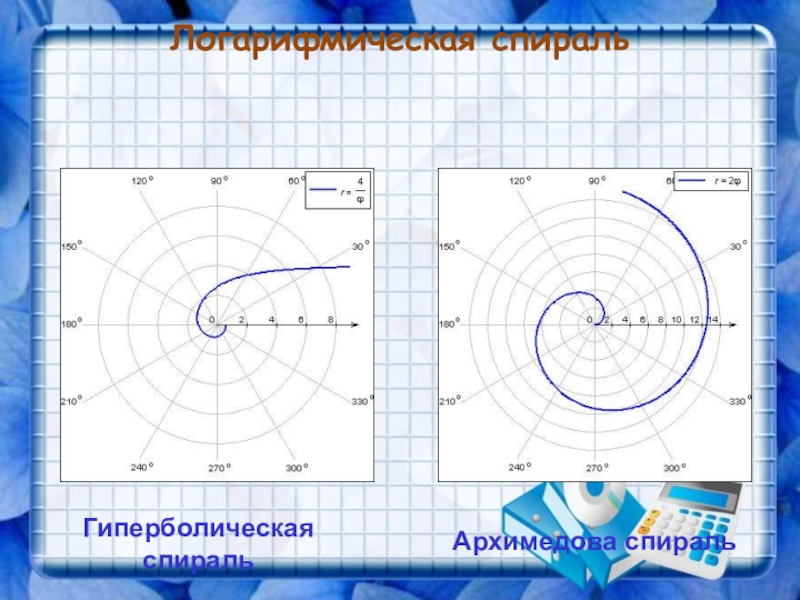
- 20. Логарифмическая спираль Архимедова спиральГиперболическая спираль
- 21. Логарифмическая спираль
- 22. Логарифмическая спираль Первым ученым, открывшим эту
- 23. Логарифмическая спираль По логарифмическим спиралям выстраиваются цветки в соцветиях подсолнечника
- 24. Логарифмическая спираль Раковины морских животных
- 25. Логарифмическая спираль Рога таких млекопитающих как архары (горные козлы), закручены по логарифмической спирали
- 26. Логарифмическая спираль По логарифмической спирали формируется тело циклона
- 27. Логарифмическая спираль Даже пауки, сплетая паутину, закручивают нити вокруг центра по логарифмической спирали.
- 28. Логарифмическая спираль улиткаЧеловеческое
- 29. Логарифмическая спираль По логарифмическим спиралям
- 30. Логарифм и ощущения! Человеческий организм способен
- 31. Решение уравнения на выборБазовый уровеньПовышенный уровеньВысокий уровень
- 32. 1. Логарифмом
- 33. Логарифмы в космосе
- 34. Яркость звезд составляет геометрическую прогрессию со знаменателем
- 35. н о
- 36. Стихотворение американского математика Мориса Клайна: “Музыка
- 37. Спасибо за урок!
Слайд 2обобщить понятие логарифма; повторить
определение логарифма, свойства
равнений;
- развивать математическое мышление; технику
вычисления; умение логически мыслить
и рационально работать; интерес к предмету;
- воспитывать познавательную активность, чувство
ответственности, уважения друг к другу.
Цели урока:
Слайд 6ДЖОН НЕПЕР
(1550-1617)
Шотландский математик –
изобретатель логарифмов.
В 1590-х годах
логарифмических вычислений
и составил первые таблицы
логарифмов, однако свой знаменитый труд
“Описание удивительных таблиц логарифмов” опубликовал лишь в 1614 году.
Ему принадлежит определение логарифмов, объяснение их свойств, таблицы логарифмов синусов, косинусов, тангенсов и приложения логарифмов в сферической тригонометрии.
Слайд 7ПАЛОЧКИ НЕПЕРА
НЕПЕР ПРЕДЛОЖИЛ
В 1617 ГОДУ ДРУГОЙ
(НЕ ЛОГАРИФМИЧЕСКИЙ)
СПОСОБ ПЕРЕМНОЖЕНИЯ ЧИСЕЛ.
ИНСТРУМЕНТ, ПОЛУЧИВШИЙ
НАЗВАНИЕ ПАЛОЧКИ (ИЛИ КОСТЯШКИ) НЕПЕРА,
СОСТОЯЛ ИЗ ТОНКИХ ПЛАСТИН, ИЛИ БЛОКОВ. КАЖДАЯ
СТОРОНА БЛОКА НЕСЕТ ЧИСЛА, ОБРАЗУЮЩИЕ
МАТЕМАТИЧЕСКУЮ ПРОГРЕССИЮ. МАНИПУЛЯЦИИ С
БЛОКАМИ ПОЗВОЛЯЮТ ИЗВЛЕКАТЬ КВАДРАТНЫЕ И
КУБИЧЕСКИЕ КОРНИ, А ТАКЖЕ УМНОЖАТЬ И ДЕЛИТЬ
БОЛЬШИЕ ЧИСЛА.
Слайд 8ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА
В 1614 году шотландский математик Джон Непер изобрел таблицы
Логарифмы очень упрощают деление и умножение.
Например, для умножения двух чисел складывают их логарифмы, результат находят в таблице логарифмов.
В дальнейшем им была изобретена логарифмическая
линейка, которой пользовались до 70-х годов прошлого века.
Слайд 9Математический диктант
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
lg 10
lg 1
lg 50 + lg 2
lg 4 + lg 25
Слайд 10Ответы:
1. 2
2. 4
3. - 1
5. 2
6. 25
7. 2
8. 2
9. 8
10. 125
11. 64
12. 9
1. 2
2. 3
3. - 1
4. 0
5. 5
6. 8
7. 2
8. 3
9. 16
10. 81
11. 125
12. 12
Слайд 12Company Logo
www.themegallery.com
Сферы применения
Логарифм
Применяется
В
Литера
туре
В
музыке
В биоло
гии
В
астрономии
В
логике
Слайд 13Company Logo
www.themegallery.com
В музыке
Известный физик Эйхенвальд вспоминал:
“Товарищ мой по гимназии любил
Представьте же себе, как неприятно был поражен мой товарищ, когда я доказал ему, что, играя по клавишам современного рояля, он играет, собственно говоря, на логарифмах”.
И действительно, так называемые ступени темперированной хроматической гаммы (12- звуковой) частот звуковых колебаний представляют собой логарифмы. Только основание этих логарифмов равно 2 (а не 10, как принято в других случаях).
Слайд 14Ноте «до» соответствует частота, равная n колебаниям в секунду.
В октаве частота
Тогда ноте «до» 1-й октавы будут соответствовать 2n колебания в
секунду, а ноте «до» 3-й октавы - колебания в секунду и т.д.
Обозначим все ноты хроматической гаммы номерами р.
Частоту любого звука можно выразить формулой
Слайд 16Принимая частоту самого низкого «до» за единицу n=1 и приводя логарифмы
Слайд 17Company Logo
www.themegallery.com
В литературе
Любопытная задача, взятая из книги “Господа Головлевы” Салтыкова-Щедрина:
“Порфирий Владимирович
Предполагая, что Порфирию в момент расчета было 50 лет, и, сделав допущение, что он произвел вычисления правильно (допущения маловероятное, т.к. едва ли Головлев знал логарифмы и умел вычислять сложные проценты), требуется установить, сколько % платил в то время ломбард.
Слайд 18
Логарифм и ощущения!
Человеческий организм способен испытывать различные ощущения. Интересно, что наш
Ощущения, воспринимаемые органами чувств человека, могут вызываться различными раздражениями, отличающимися друг от друга в миллиарды раз. Удары молота о стальную плиту в сто раз громче, чем шелест листьев, а яркость вольтовой дуги в миллионы раз превосходит яркость какой-нибудь слабой звезды на ночном небосклоне. Но никакие физиологические процессы не дают такого диапазона ощущений. Опыты показали, что организм как бы «логарифмирует» полученные им раздражения, т. е. величина ощущений приблизительно пропорциональна десятичному логарифму величины раздражения.
Фехнер математически выразил тот факт, что ощущение изменяется гораздо медленнее, чем растет сила раздражения
Возьмём для примера чай: стакан чая с двумя кусками сахара воспринимается раза в два более сладким, чем чай с одним куском сахара; но чай с 20 кусками сахара едва ли покажется заметно слаще, чем с 10 кусками...
Как видим, логарифмы вторгаются и в область психологии.
Слайд 19Логарифмическая спираль
Спираль – это плоская кривая линия, многократно обходящая одну из
Слайд 21Логарифмическая спираль
является траекторией точки, которая движется вдоль равномерно вращающейся
прямой, удаляясь от полюса
со скоростью,
пропорциональной
пройденному
расстоянию.
Т.о. в логарифмической спирали
углу поворота пропорционален
логарифм этого расстояния.
Слайд 22Логарифмическая спираль
Первым ученым, открывшим эту удивительную кривую, был
французский математик
(1596-1650гг.)
Слайд 23Логарифмическая спираль
По логарифмическим спиралям выстраиваются
цветки в соцветиях подсолнечника
Слайд 24Логарифмическая спираль
Раковины морских животных могут расти лишь в
Слайд 25Логарифмическая спираль
Рога таких млекопитающих как архары (горные козлы), закручены
Слайд 27Логарифмическая спираль
Даже пауки, сплетая паутину, закручивают нити вокруг центра
Слайд 28Логарифмическая спираль
улитка
Человеческое ухо – это маленькое чудо!
Улитка
ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ!
Слайд 29Логарифмическая спираль
По логарифмическим спиралям закручены многие галактики, в частности
Слайд 30
Логарифм и ощущения!
Человеческий организм способен испытывать различные ощущения. Интересно, что наш
Ощущения, воспринимаемые органами чувств человека, могут вызываться различными раздражениями, отличающимися друг от друга в миллиарды раз. Удары молота о стальную плиту в сто раз громче, чем шелест листьев, а яркость вольтовой дуги в миллионы раз превосходит яркость какой-нибудь слабой звезды на ночном небосклоне. Но никакие физиологические процессы не дают такого диапазона ощущений. Опыты показали, что организм как бы «логарифмирует» полученные им раздражения, т. е. величина ощущений приблизительно пропорциональна десятичному логарифму величины раздражения.
Психофизический закон Фехнера гласит: величина ощущения пропорциональна логарифму величины раздражения.
Возьмём для примера чай: стакан чая с двумя кусками сахара воспринимается раза в два более сладким, чем чай с одним куском сахара; но чай с 20 кусками сахара едва ли покажется заметно слаще, чем с 10 кусками...
Как видим, логарифмы вторгаются и в область психологии.
Слайд 32 1. Логарифмом числа b
называется …………….. степени, в которую
нужно……………. основание а, чтобы
получить число b.
2. Основание и число, стоящее под знаком
логарифма, должны быть………….
3. Если основание а =….., то такой логарифм
называется десятичным и обозначается lg b.
основанию
показатель
возвести
положительными
10
Продолжи предложение.....
Слайд 34Яркость звезд составляет геометрическую прогрессию со знаменателем 2,5 легко понять, что
Оценивая яркость звезд, астроном оценивает таблицей логарифмов составленной при основании 2,5.
Аналогично оценивается и громкость шума. Вредное влияние промышленных шумов на здоровье рабочих и производстве труда.
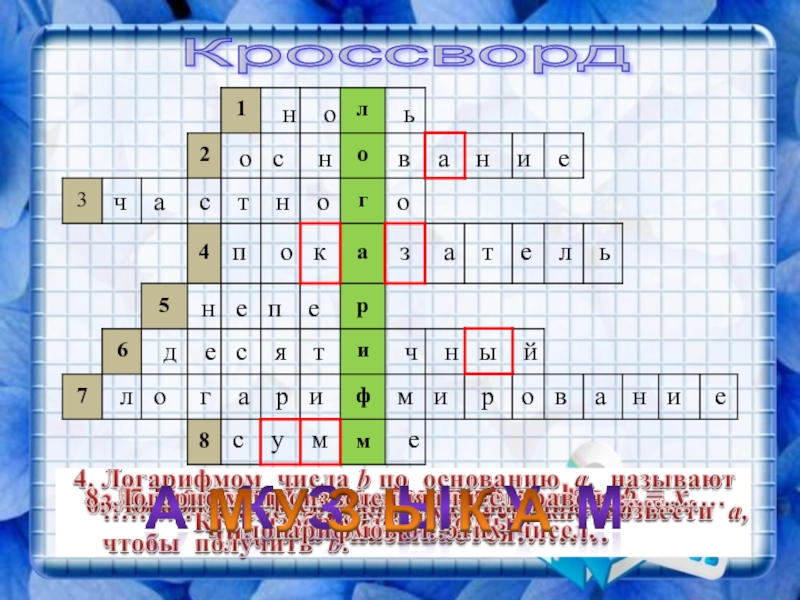
Слайд 35н о ь
ч а
с у м е
о с н в а н и е
п о к з а т е л ь
н е п е
д е с я т ч н ы й
л о г а р и м и р о в а н и е
Кроссворд
Слайд 36
Стихотворение американского математика Мориса Клайна:
“Музыка может возвышать или умиротворять душу
Живопись –
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни,
А математика способна достичь всех этих целей”.