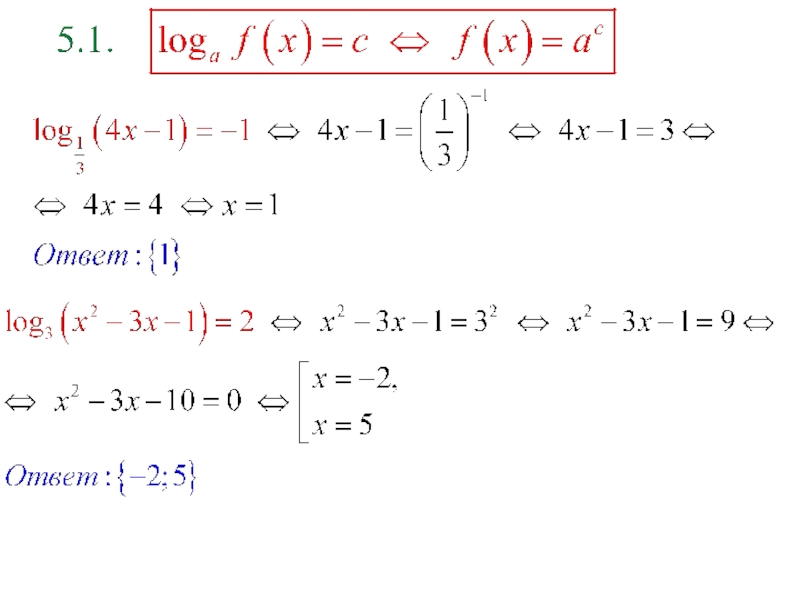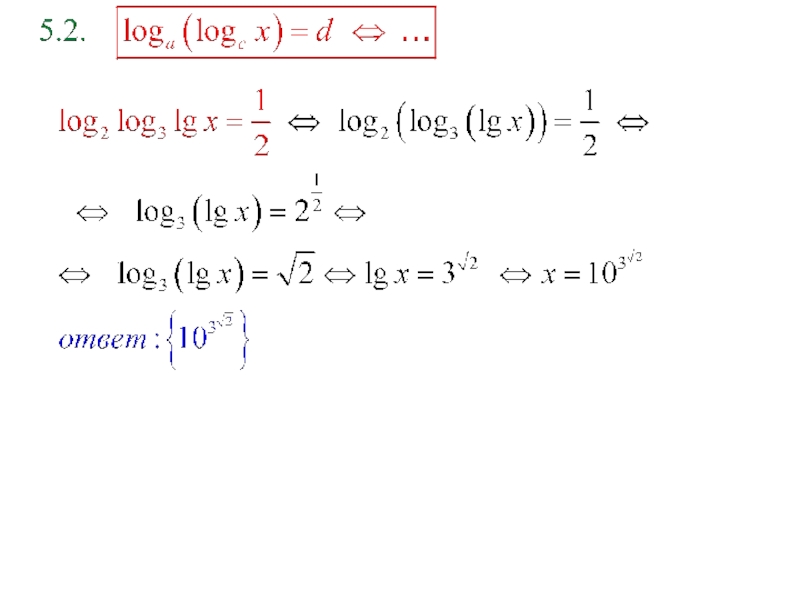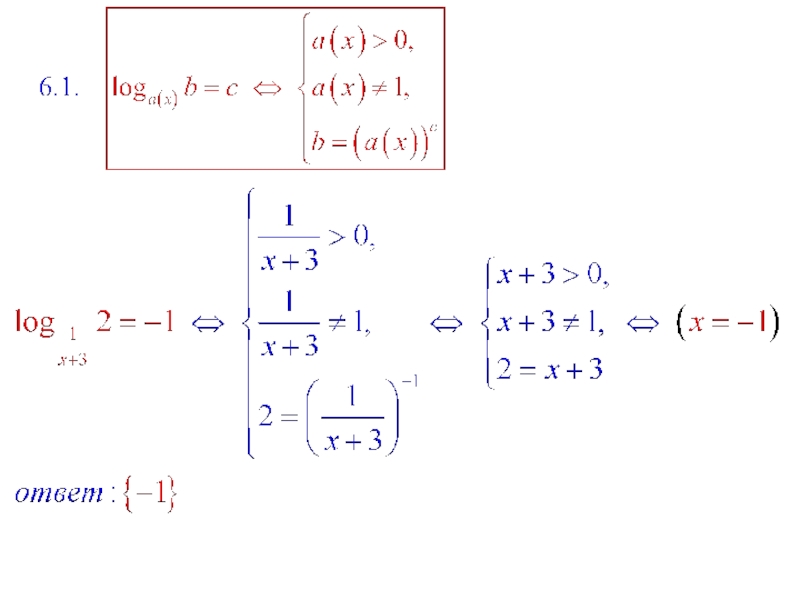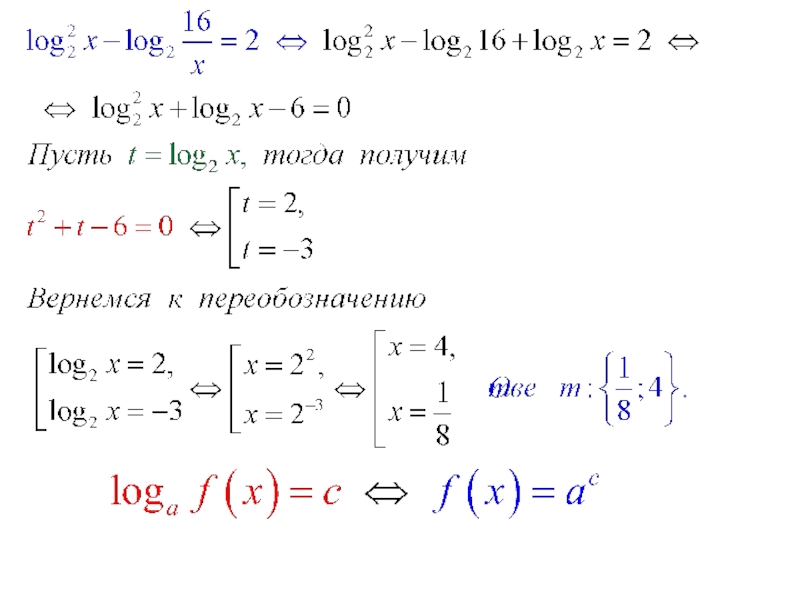ShareSlide^ru

Презентация, доклад по алгебре и началам математического анализа по теме Логарифмические уравнения. Теория

Содержание

1. Презентация по алгебре и началам математического анализа по теме Логарифмические уравнения. Теория
2. п.1. Уравнения вида Уравнение
3. Слайд 3
4. Слайд 4
5. Слайд 5
6. п.2. Уравнения вида Уравнение
7. Слайд 7
8. п.3. Уравнения вида Уравнение
9. Слайд 9
10. Слайд 10
11. п.4. Уравнения вида Уравнение
12. Слайд 12
13. Слайд 13
14. Слайд 14
15. Слайд 15
16. Слайд 16
17. Слайд 17
18. Слайд 18
19. Слайд 19
20. Слайд 20
21. Слайд 21
22. Слайд 22
23. 7. Уравнения вида
24. 8. Уравнения вида
25. 9. Уравнения на применение основного логарифмического тождества
26. Слайд 26
27. 10. Уравнения на применение формул для логарифмов произведения, частного и степени
28. Слайд 28
29. Слайд 29
30. Слайд 30
31. Слайд 31
32. Слайд 32
33. Слайд 33
34. Слайд 34
35. Слайд 35
36. 12. Переход к другому основанию Следствие:При решении данных уравнений используется формула перехода к другому основанию:
37. Слайд 37
38. Слайд 38
39. Слайд 39
40. 13. Уравнения вида Как правило, уравнение такого вида решается логарифмированием обеих частей по основанию а.
41. 15. Уравнения, содержащие выражение вида При решении уравнений такого вида используется формула
42. 15. Уравнения, решаемые оценкой его левой и
43. Слайд 43
44. Слайд 44
45. Слайд 45
46. Слайд 46

п.1. Уравнения вида Уравнение такого вида можно заменить равносильной системой двумя способами.Второй способ Из двух систем можно выбрать любую.Первый способ

Главная
Математика
Презентация по алгебре и началам математического анализа по теме Логарифмические уравнения. Теория

Слайд 1Логарифмические уравнения
( обзор видов
и
способов решения )

Логарифмические уравнения( обзор видов и способов решения )

Слайд 2п.1. Уравнения вида
Уравнение такого вида можно заменить

равносильной системой двумя способами.

Второй способ

Из двух систем можно выбрать любую.

Первый способ

п.1. Уравнения вида Уравнение такого вида можно заменить равносильной системой двумя способами.Второй способ Из

Слайд 3

Слайд 4

Слайд 5

Слайд 6п.2. Уравнения вида
Уравнение такого вида можно заменить

равносильной системой двумя способами.

Второй способ

Из двух систем можно выбрать любую.

Первый способ

п.2. Уравнения вида Уравнение такого вида можно заменить равносильной системой двумя способами.Второй способ Из

Слайд 7

Слайд 8п.3. Уравнения вида
Уравнение такого вида можно заменить

равносильной системой двумя способами.

Второй способ

Из двух систем можно выбрать любую.

Первый способ

п.3. Уравнения вида Уравнение такого вида можно заменить равносильной системой двумя способами.Второй способ Из

Слайд 9

Слайд 10

Слайд 11п.4. Уравнения вида
Уравнение такого вида можно заменить

равносильной системой двумя способами.

Второй способ

Из двух систем можно выбрать любую.

Первый способ

п.4. Уравнения вида Уравнение такого вида можно заменить равносильной системой двумя способами.Второй способ Из

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Слайд 18

Слайд 19

Слайд 20

Слайд 21

Слайд 22

Слайд 237. Уравнения вида

7. Уравнения вида

Слайд 248. Уравнения
вида

8. Уравнения вида

Слайд 25
9. Уравнения на применение основного
логарифмического тождества

9. Уравнения на применение основного логарифмического тождества

Слайд 26

Слайд 2710. Уравнения на применение формул
для логарифмов произведения, частного и степени

10. Уравнения на применение формул для логарифмов произведения, частного и степени

Слайд 28

Слайд 29

Слайд 30

Слайд 31

Слайд 32

Слайд 33

Слайд 34

Слайд 35

Слайд 3612. Переход к другому основанию

Следствие:

При решении данных уравнений используется
формула

перехода к другому основанию:

12. Переход к другому основанию Следствие:При решении данных уравнений используется формула перехода к другому основанию:

Слайд 37

Слайд 38

Слайд 39

Слайд 4013. Уравнения вида
Как правило, уравнение такого вида решается
логарифмированием

обеих частей по основанию а.

13. Уравнения вида Как правило, уравнение такого вида решается логарифмированием обеих частей по основанию а.

Слайд 4115. Уравнения, содержащие выражение вида
При решении уравнений такого

вида используется формула

15. Уравнения, содержащие выражение вида При решении уравнений такого вида используется формула

Слайд 4215. Уравнения, решаемые оценкой его левой и
правой частей или при

использовании свойств функций

15. Уравнения, решаемые оценкой его левой и правой частей или при использовании свойств функций

Слайд 43

Слайд 44

Слайд 45

Слайд 46

Скачать презентацию

Что такое shareslide.ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть