- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Опыты с равновозможными элементарными событиями
Содержание
- 1. Презентация Опыты с равновозможными элементарными событиями
- 2. Элементарные события случайного опыта называются равновозможными, если
- 3. НазадСлучайный опыт (случайный эксперимент) - математическая абстракция,
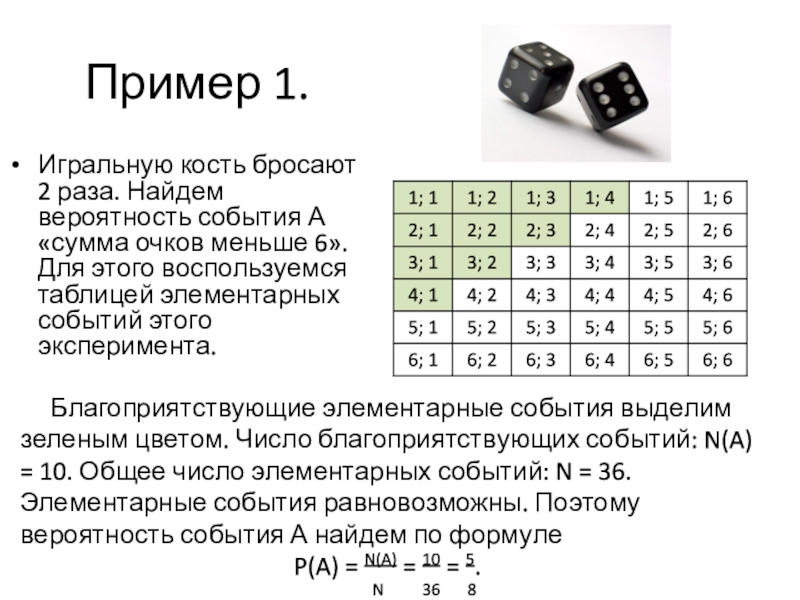
- 4. Пример 1.Игральную кость бросают 2 раза. Найдем
- 5. Пример 2.Дважды бросают симметричную монету.
- 6. Упражнение 1.Бросают одну игральную кость. Вычислите вероятность
- 7. Решение:а) P(A)=5;б) P(A)=1;в) P(A)=3=1.666Упражнение 2.2Бросают одну игральную
- 8. Назад Делителем натурального числа a называют натуральное число,
- 9. Кратным натурального числа a называют натуральное число,
- 10. Натуральное число называют простым, если оно имеет
- 11. Натуральные числа – это те числа, которые
- 12. Упражнение 3.Бросают симметричную монету 2 раза. Равные
- 13. Упражнение 4.Бросают две игральных кости: желтую и
- 14. Упражнение 5.Пятачок идет из своего дома к
- 15. Упражнение 6.В коробке лежат 24 одинаковые ручки.
- 16. Упражнение 7.На день рождения к Паше пришли
- 17. Подведение итогов.Вы узнали, как найти вероятности событий
Слайд 2
Элементарные события случайного опыта называются равновозможными, если все они имеют одинаковые
N – количество равновозможных элементарных событий некоторого опыта.
Вероятности таких элементарных событий одинаковы и в сумме равны 1 => вероятность каждого элементарного события равна 1/N.
N(A) – количество элементарных событий, благоприятствующих событию A.
P(A) = N(A)
N
P(A) = N(A)
Правило: если в опыте все элементарные события равновозможны, то вероятность произвольного события равна отношению числа элементарных событий, благоприятствующих этому событию, к общему числу элементарных событий.
N
Слайд 3
Назад
Случайный опыт (случайный эксперимент) - математическая абстракция, описывающая реальный опыт, который
Слайд 4Пример 1.
Игральную кость бросают 2 раза. Найдем вероятность события А «сумма
Слайд 5Пример 2.
Дважды бросают симметричную монету.
Найдем вероятность того, что
Обозначим выпадение орла буквой О, а решки – буквой Р и выпишем все элементарные события:
ОО, ОР, РО и РР.
Всего элементарных событий четыре. Так как монета симметричная, эти события равновозможны. Из них ровно два события ОО и РР благоприятствуют указанному событию. Вероятность получить оба раза одну сторону равна ²/₄=¹/₂.
Слайд 6Упражнение 1.
Бросают одну игральную кость. Вычислите вероятность события:
а) «выпало четное число
б) «выпало число очков, кратное трем»;
в) «выпало число очков, большее 3»;
г) «выпало число очков, кратное 7».
Решение:
а) P(A)=N(A)=3=1;
б) P(A)=2=1;
в) P(A)=3=1;
г) P(A)=0=0 – это событие невозможное.
N
6
2
6
3
6
2
6
Слайд 7
Решение:
а) P(A)=5;
б) P(A)=1;
в) P(A)=3=1.
6
6
6
Упражнение 2.
2
Бросают одну игральную кость. Вычислите вероятность события:
а)
б) «выпавшее число очков кратно 5»;
в) «выпавшее число очков является простым числом».
Упражнение 2.
Бросают одну игральную кость. Вычислите вероятность события:
а) «выпавшее число очков является делителем числа 12»;
б) «выпавшее число очков кратно 5»;
в) «выпавшее число очков является простым числом».
Слайд 8
Назад
Делителем натурального числа a называют натуральное число, на которое a делится
Пример: число 24 имеет 8 делителей:
1; 2; 3; 4; 6; 8; 12; 24.
Число 1 является делителем любого натурального числа.
Слайд 9
Кратным натурального числа a называют натуральное число, которое делится на a
Пример. Первые пять чисел, кратные 8:
8; 16; 24; 32; 40.
Наименьшим из кратных натурального числа является само это число.
Назад
Слайд 10
Натуральное число называют простым, если оно имеет только два делителя: единицу
Число 1 имеет только один делитель – само это число, - поэтому его не относят к простым.
Первыми десятью простыми числами являются 2; 3; 5; 7; 11; 13; 17; 19; 23; 29.
Назад
Слайд 11
Натуральные числа – это те числа, которые используются для счета предметов
Натуральный ряд бесконечен.
1 – самое маленькое натуральное число.
Делитель
Кратное
Простое число
Упражнение 2
Упражнение 3
Слайд 12Упражнение 3.
Бросают симметричную монету 2 раза. Равные ли вероятности имеют события
Найдите вероятности этих событий.
Решение:
ОО; ОР; РО; РР.
P(A)=1/4;
P(B)=2/4=1/2.
Ответ: 1/4; 1/2; эти вероятности не равны.
A
B
Слайд 13Упражнение 4.
Бросают две игральных кости: желтую и зеленую. Вычислите вероятность события:
а)
б) «сумма очков на обеих костях равна 11»;
в) «на желтой кости выпало больше очков, чем на зеленой»;
г) «числа очков на костях различаются не больше, чем на 2»;
д) «произведение очков на обеих костях равно 10»;
е) «сумма очков на обеих костях делится на 3».
Решение:
а) P(A)= 6 =1;
б) P(A)= 2 =1 ;
в) P(A)=15=5 ;
г) P(A)=24=2;
д) P(A)= 2 =1 ;
е) P(A)=12=1.
36
36
36
36
36
36
6
18
12
3
3
18
Слайд 14Упражнение 5.
Пятачок идет из своего дома к дому Винни-Пуха, а Винни-Пух
Решение:
а) P(встречи)=1/2.
б) в – верхняя
с – средняя
н – нижняя
вв вс вн
св сс сн
нв нс нн
P(встречи)=3/9=1/3.
в) В этом случае шесть дорожек, следовательно опыт аналогичен бросанию игральной кости дважды, значит число элементарных событий опыта N=62=36.
Число благоприятствующих элементарных событий N(встречи)=6 (по диагонали).
P(встречи)=6/36=1/6.
Ответ: 1/2; 1/3; 1/6.
Слайд 15Упражнение 6.
В коробке лежат 24 одинаковые ручки. Из них 13 красных,
а) «извлеченная ручка красная»;
б) «извлеченная рука не зеленая»;
в) «извлеченная ручка либо синяя, либо зеленая»;
г) «извлеченная ручка либо красная, либо синяя».
Решение:
а) P(A)=13, т.к. красных ручек 13, N(A)=13, N=24;
б) P(A)=19;
в) P(A)=11;
г) P(A)=19.
24
24
24
24
Слайд 16Упражнение 7.
На день рождения к Паше пришли две Маши и два
Решение:
N=6
N(A)=2
P(A)=2/6=1/3
Слайд 17Подведение итогов.
Вы узнали, как найти вероятности событий в опыте, в котором
Домашнее задание.
Читать пункт 31 учебника.
Выучить ответ на вопрос после пункта наизусть.
Выполнить письменно №№7, 9, 12, 19.