- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад ОБРАТНАЯ МАТРИЦА по дисциплине ЕН.01 МАТЕМАТИКА 2 курс СПО
Содержание
- 1. Презентация ОБРАТНАЯ МАТРИЦА по дисциплине ЕН.01 МАТЕМАТИКА 2 курс СПО
- 2. Определение Произведением матрицы Аmхn на матрицу Bnхk называется матрица Cmхk такая, что элемент
- 3. Задание. Найти A*B , если Решение. Так как
- 4. Матрица называется обратной матрицей для квадратной матрицы А, если Обратная матрица
- 5. Составим алгоритм нахождения обратной матрицы с использованием равенства
- 6. Умножаем каждый элемент матрицы на
- 7. : 6 2. Найдём все алгебраические
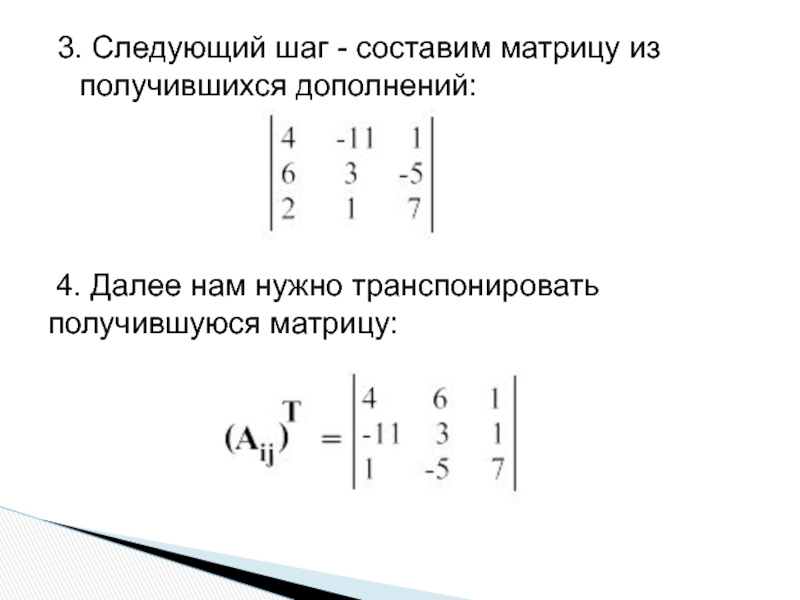
- 8. 3. Следующий шаг - составим матрицу из получившихся дополнений: 4. Далее нам нужно транспонировать получившуюся матрицу:
- 9. 5. Умножаем эту матрицу на число, обратное определителю, то есть на 1/26: 6. Выполним проверку:
- 10. Систему линейных алгебраических уравнений можно представить в
- 11. СПАСИБО ЗА ВНИМАНИЕ
Определение Произведением матрицы Аmхn на матрицу Bnхk называется матрица Cmхk такая, что элемент матрицы , стоящий в i-ой строке и j-ом столбце, т.е. элемент , равен сумме произведений элементов i-ой строки матрицы A на соответствующие элементы j-ого столбца матрицы B .Произведение матриц
Слайд 1Произведение матриц. Обратная матрица.
Толоконников А.В.
Преподаватель КРК «Интеграл»
КРК «Интеграл»
КУРСАВКА 2016
Слайд 2Определение
Произведением матрицы Аmхn на матрицу Bnхk называется матрица Cmхk такая, что элемент матрицы , стоящий в i-ой строке
и j-ом столбце, т.е. элемент , равен сумме произведений элементов i-ой строки матрицы A на соответствующие элементы j-ого столбца матрицы B .
Произведение матриц
Слайд 3Задание. Найти A*B , если
Решение. Так как
, а , то в результате получим матрицу , т.е. матрицу вида
Найдем элементы данной матрицы:
Таким образом, получаем, что:
Или короче:
Найдем элементы данной матрицы:
Таким образом, получаем, что:
Или короче:
Ответ.
Слайд 5Составим алгоритм нахождения обратной матрицы с использованием равенства
.
Вычисляем определитель матрицы А и убеждаемся, что он отличен от нуля (в противном случае матрица А необратима).
Строим - матрицу из алгебраических дополнений элементов .
Транспонируем матрицу , тем самым получаем .
Вычисляем определитель матрицы А и убеждаемся, что он отличен от нуля (в противном случае матрица А необратима).
Строим - матрицу из алгебраических дополнений элементов .
Транспонируем матрицу , тем самым получаем .
АЛГОРИТМ НАХОЖДЕНИЯ ОБРАТНОЙ МАТРИЦЫ
Слайд 6Умножаем каждый элемент матрицы на число
.
Этой операцией завершается нахождение обратной матрицы .
Для проверки результата, проводим вычисление произведения . Если , то обратная матрица найдена верно, в противном случае где-то была допущена ошибка.
Этой операцией завершается нахождение обратной матрицы .
Для проверки результата, проводим вычисление произведения . Если , то обратная матрица найдена верно, в противном случае где-то была допущена ошибка.
Слайд 7
:
6
2. Найдём все алгебраические дополнения.
Пример: найти матрицу, обратную матрице
А=
1. Определитель матрицы . Следовательно матрица А имеет обратную.
Слайд 83. Следующий шаг - составим матрицу из получившихся дополнений:
4.
Далее нам нужно транспонировать получившуюся матрицу:
Слайд 9
5. Умножаем эту матрицу на число, обратное определителю, то есть на
1/26:
6. Выполним проверку:
6. Выполним проверку:
Слайд 10Систему линейных алгебраических уравнений можно представить в виде произведения матриц А*Х=В,
где А матрица, составленная из коэффициентов при неизвестных;
Х - матрица-столбец неизвестных;
В - матрица-столбец свободных членов.
Тогда Х=А-1*В, где А-1матрица, обратная матрице А
Х - матрица-столбец неизвестных;
В - матрица-столбец свободных членов.
Тогда Х=А-1*В, где А-1матрица, обратная матрице А
Решение СЛАУ матричным способом