: Туровец Т.С., учитель математики
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Необычные способы счета
Содержание
- 1. Презентация Необычные способы счета
- 2. Объект исследования:алгоритмы счетаПредмет исследования:процесс вычисленийГипотеза:овладение приемами устного
- 3. Методы исследования: поисковый метод с использованием научной и
- 4. Цель работы:изучить различные способы вычислений и проверить гипотезу.
- 5. Задачи:изучить научную и учебную литературу, согласно теме
- 6. АктуальностьАктуальность данной темы заключается в том, что
- 7. Исследуемые способы вычисления:Умножение на пальцахУмножение удвоениемКрестьянский способ
- 8. УМНОЖЕНИЕ НА ПАЛЬЦАХ Умножали на пальцах
- 9. Растопырьте пальцы на обеих руках и поверните
- 10. Еще пример: нужно вычислить 9·8=?. По ходу
- 11. КРЕСТЬЯНСКИЙ СПОСОБ УМНОЖЕНИЯ Русские крестьяне применяли следующий способ
- 12. УМНОЖЕНИЕ НА 11 1 способ. Чтобы число
- 13. УМНОЖЕНИЕ НА 9 Чтобы умножить число на
- 14. УМНОЖЕНИЕ ТРЁХЗНАЧНОГО ЧИСЛА НА
- 15. КВАДРАТ ДВУЗНАЧНЫХ ЧИСЕЛ, ОКАНЧИВАЮЩИХСЯ НА 5
- 16. КВАДРАТ ДВУЗНАЧНЫХ ЧИСЕЛ, НАЧИНАЮЩИХСЯ С 5-ТИ
- 17. Практическая частьИзучив в литературных и Интернет источниках
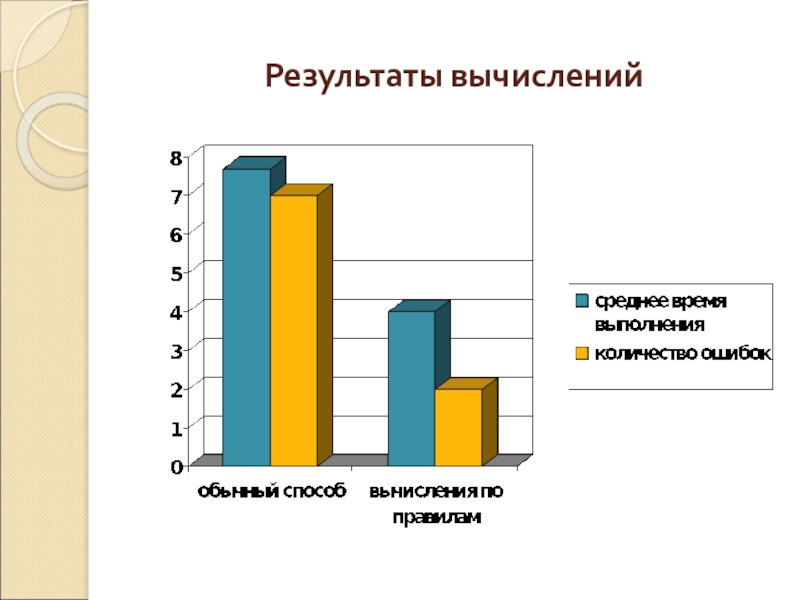
- 18. Результаты вычислений
- 19. Вывод:Работая над этой темой, я узнала, что
- 20. Спасибо за внимание!
Объект исследования:алгоритмы счетаПредмет исследования:процесс вычисленийГипотеза:овладение приемами устного счета позволит повысить качество и скорость вычислений пятиклассников
Слайд 2Объект исследования:
алгоритмы счета
Предмет исследования:
процесс вычислений
Гипотеза:
овладение приемами устного счета позволит повысить качество
и скорость вычислений пятиклассников
Слайд 3Методы исследования:
поисковый метод с использованием научной и учебной литературы, а также поиск
необходимой информации в сети Интернет;
практический метод выполнения вычислений с применением нестандартных алгоритмов счета;
анализ полученных в ходе исследования данных.
практический метод выполнения вычислений с применением нестандартных алгоритмов счета;
анализ полученных в ходе исследования данных.
Слайд 5Задачи:
изучить научную и учебную литературу, согласно теме исследования;
проанализировать нестандартные способы счета;
научиться
применять на практике различные способы вычислений;
развить навыки самостоятельной работы: поиск информации, отбор и оформление найденного материала;
провести констатирующий эксперимент, провести тест среди учащихся 5 класса;
сделать вывод о подтверждении или опровержении выдвинутой гипотезы.
развить навыки самостоятельной работы: поиск информации, отбор и оформление найденного материала;
провести констатирующий эксперимент, провести тест среди учащихся 5 класса;
сделать вывод о подтверждении или опровержении выдвинутой гипотезы.
Слайд 6Актуальность
Актуальность данной темы заключается в том, что использование нестандартных приемов в
формировании вычислительных навыков усиливает интерес учащихся к математике и содействует развитию математических способностей.
Слайд 7Исследуемые способы вычисления:
Умножение на пальцах
Умножение удвоением
Крестьянский способ умножения
Умножение способом «маленький замок»
Умножение
на 11, 9, 50, 101
Квадрат двузначных чисел, начинающихся с 5-ти; квадрат двузначных чисел, оканчивающихся на 5
Египетский способ умножения
Умножение чисел методом «ревность»
Новый способ умножения (таблица Оконешникова)
Квадрат двузначных чисел, начинающихся с 5-ти; квадрат двузначных чисел, оканчивающихся на 5
Египетский способ умножения
Умножение чисел методом «ревность»
Новый способ умножения (таблица Оконешникова)
Слайд 8УМНОЖЕНИЕ НА ПАЛЬЦАХ
Умножали на пальцах однозначные числа от 6 до 9.
Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходил число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. После этого брали столько десятков, сколько вытянуто пальцев на обеих руках, и прибавляли к этому числу произведение загнутых пальцев на первой и второй руке.
Пример: 8 ∙ 9 = 72
Пример: 8 ∙ 9 = 72
Слайд 9 Растопырьте пальцы на обеих руках и поверните руки ладонями от себя.
Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки .
УМНОЖЕНИЕ НА 9
Слайд 10Еще пример: нужно вычислить 9·8=?. По ходу дела скажем, что в
качестве "счетной машинки" не обязательно могут выступать пальцы рук. Возьмите, к примеру, 10 клеточек в тетради. Зачеркиваем 8-ю клеточку. Слева осталось 7 клеточек, справа - 2 клеточки. Значит 9·8=72. Все очень просто.
7 клеток 2 клетки
7 клеток 2 клетки
Слайд 11КРЕСТЬЯНСКИЙ СПОСОБ УМНОЖЕНИЯ
Русские крестьяне применяли следующий способ умножения: Пусть надо умножить
37 на 32. Составим два столбца чисел, - один удвоением, начиная с числа 37, другой раздвоением, начиная с числа 32:
37……….32
74……….16
148……….8
296……….4
592……….2
1184……….1
Произведение всех пар соответственных чисел одинаковое, поэтому
37 ∙ 32 = 1184 ∙ 1 = 1184
37……….32
74……….16
148……….8
296……….4
592……….2
1184……….1
Произведение всех пар соответственных чисел одинаковое, поэтому
37 ∙ 32 = 1184 ∙ 1 = 1184
Слайд 12УМНОЖЕНИЕ НА 11
1 способ. Чтобы число умножить на 11, к нему
приписывают 0 и прибавляют исходное число. Например:
47 * 11 = 470 + 47 = 517
243 * 11 = 2430 + 243 = 2673
2 способ. Если хочешь умножить число на 11, то поступай так: запиши число, которое нужно умножить на 11, а между цифрами исходного числа вставь сумму этих цифр. Если сумма получается двузначное число, то 1 прибавляем к первой цифре исходного числа. Например:
45 * 11 = 4(4+5)5 = 495
Такой способ подходит только для умножения двузначных чисел
47 * 11 = 470 + 47 = 517
243 * 11 = 2430 + 243 = 2673
2 способ. Если хочешь умножить число на 11, то поступай так: запиши число, которое нужно умножить на 11, а между цифрами исходного числа вставь сумму этих цифр. Если сумма получается двузначное число, то 1 прибавляем к первой цифре исходного числа. Например:
45 * 11 = 4(4+5)5 = 495
Такой способ подходит только для умножения двузначных чисел
Слайд 13УМНОЖЕНИЕ НА 9
Чтобы умножить число на 9, к нему приписывают 0
и отнимают исходное число. Например,
241 * 9 = 2410 – 241 = 2169
847 * 9 = 8470 – 847 = 7623
241 * 9 = 2410 – 241 = 2169
847 * 9 = 8470 – 847 = 7623
Слайд 14
УМНОЖЕНИЕ ТРЁХЗНАЧНОГО ЧИСЛА НА 101
Например 125 * 101.
(увеличиваем первый множитель
на число его сотен и приписываем к нему справа две последние цифры первого множителя)
125 + 1 = 126 12625
125 + 1 = 126 12625
Слайд 15
КВАДРАТ ДВУЗНАЧНЫХ ЧИСЕЛ, ОКАНЧИВАЮЩИХСЯ НА 5
ПРАВИЛО: умножают число десятков на число,
на единицу большее, и к произведению приписывают 25.
752=(7*8) в конец произведения подписываем 25 : 5625
752=(7*8) в конец произведения подписываем 25 : 5625
Слайд 16
КВАДРАТ ДВУЗНАЧНЫХ ЧИСЕЛ, НАЧИНАЮЩИХСЯ С 5-ТИ
Чтобы возвести в квадрат число, начинающееся
на 5, надо:
к 52=25 прибавить число единиц «а».
к полученному числу приписать справа квадрат единиц.
562=(25+6)*(62)=3136
592=(25+9)*(92)=3481
к 52=25 прибавить число единиц «а».
к полученному числу приписать справа квадрат единиц.
562=(25+6)*(62)=3136
592=(25+9)*(92)=3481
Слайд 17Практическая часть
Изучив в литературных и Интернет источниках приёмы устного счёта, я
отобрала самые распространённые и общедоступные. По согласованию с учителем математики, я составила математический диктант, опираясь на данные свойства. На уроке с разрешения учителя, я провела диктант в своём классе. В эксперименте принимали участие 6 человек. Трое выполняли вычисления обычными способами, а трое других учащихся выполняли вычисления по правилам, с которыми я их предварительно познакомила.
Образец диктанта:
1. 41*39
2. 26*34
3. 89²-11²
4. 45²
5. 28*11
6. 84*12
7. 79*11
8. 129*5
9. 64*18
10. 87*93
Образец диктанта:
1. 41*39
2. 26*34
3. 89²-11²
4. 45²
5. 28*11
6. 84*12
7. 79*11
8. 129*5
9. 64*18
10. 87*93
Слайд 19Вывод:
Работая над этой темой, я узнала, что существует много различных, забавных
и интересных способов вычислений. Некоторыми в различных странах пользуются до сих пор. Но не все способы удобны в использовании, особенно при умножении многозначных чисел.
Из всех найденных мною необычных способов счета более интересными показались способы умножения на 9, 11,101, 50, пальцевый счёт, возведение в квадрат двухзначных чисел, начинающихся и заканчивающихся на 5.
Самым простым мне показался метод «удвоения и раздвоения», который использовали русские крестьяне. Я его использую при умножении не слишком больших чисел (очень удобно его использовать при умножении двузначных чисел).
Заинтересовал новый способ умножения, потому что он позволяет в уме «ворочать» огромными числами.
Используя упрощенные приёмы устных вычислений я научилась производить наиболее трудоёмкие арифметические действия без применения калькулятора и компьютера.
Наша первоначальная гипотеза о том, что знание и использование приемов быстрого счета позволит существенно увеличить скорость и качество счета, подтверждается.
Из всех найденных мною необычных способов счета более интересными показались способы умножения на 9, 11,101, 50, пальцевый счёт, возведение в квадрат двухзначных чисел, начинающихся и заканчивающихся на 5.
Самым простым мне показался метод «удвоения и раздвоения», который использовали русские крестьяне. Я его использую при умножении не слишком больших чисел (очень удобно его использовать при умножении двузначных чисел).
Заинтересовал новый способ умножения, потому что он позволяет в уме «ворочать» огромными числами.
Используя упрощенные приёмы устных вычислений я научилась производить наиболее трудоёмкие арифметические действия без применения калькулятора и компьютера.
Наша первоначальная гипотеза о том, что знание и использование приемов быстрого счета позволит существенно увеличить скорость и качество счета, подтверждается.