Выполнили:
Батькова Яна Олеговна,
Ученица 11а класса МБОУ «СОШ №4»,
Галкин Александр Владимирович,
Ученик 11б класса МБОУ «СОШ №4»,
Коробейникова Луиза Максимовна,
Ученик 11а класса МБОУ «СОШ №4»,
Научный Руководитель:
Магомедов Иосиф Маграмович,
учитель математики МБОУ «СОШ №4»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад научно-исследовательской работы учащихся по теме Квадратные уравнения с параметрами
Содержание
- 1. Презентация научно-исследовательской работы учащихся по теме Квадратные уравнения с параметрами
- 2. квадратные уравнения с параметрами Цель работы:исследовать необходимые
- 3. Полученные данные, выводы: В результате исследовательской работы
- 4. План исследованийОбъект исследования: квадратные уравнения с параметрами.Предмет
- 5. ОглавлениеВведение
- 6. ВведениеИсследовательская работа посвящена одному из наиболее трудных
- 7. §1. Теоремы о расположении корней квадратного
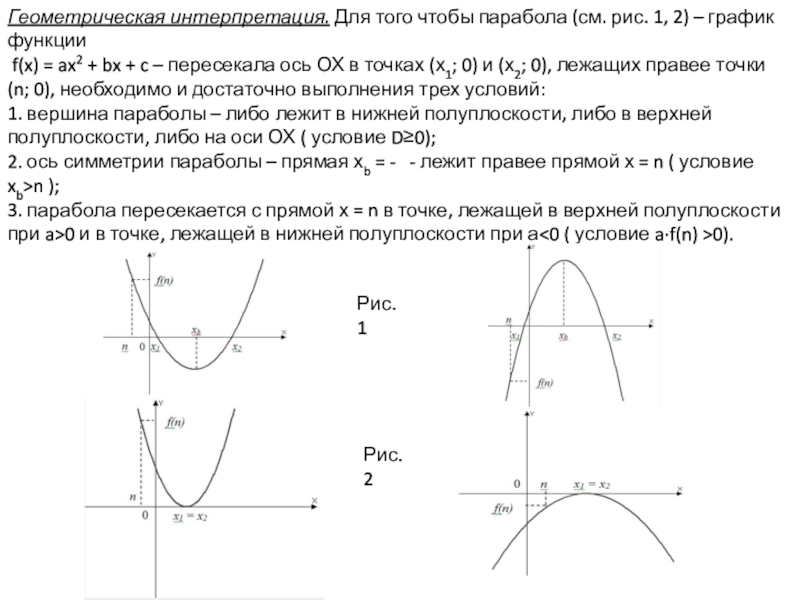
- 8. Геометрическая интерпретация. Для того чтобы парабола (см.
- 9. Доказательство теоремы 1.Достаточность. Так как D ≥
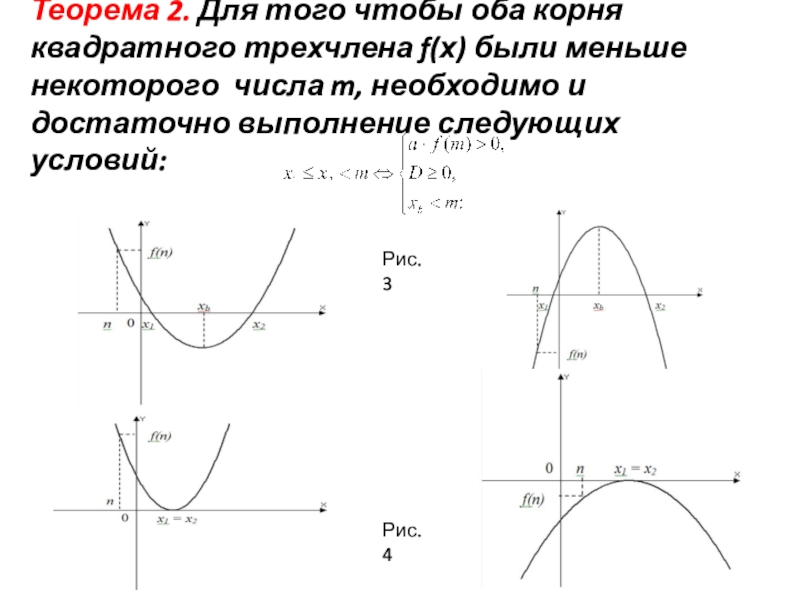
- 10. Теорема 2. Для того чтобы оба корня
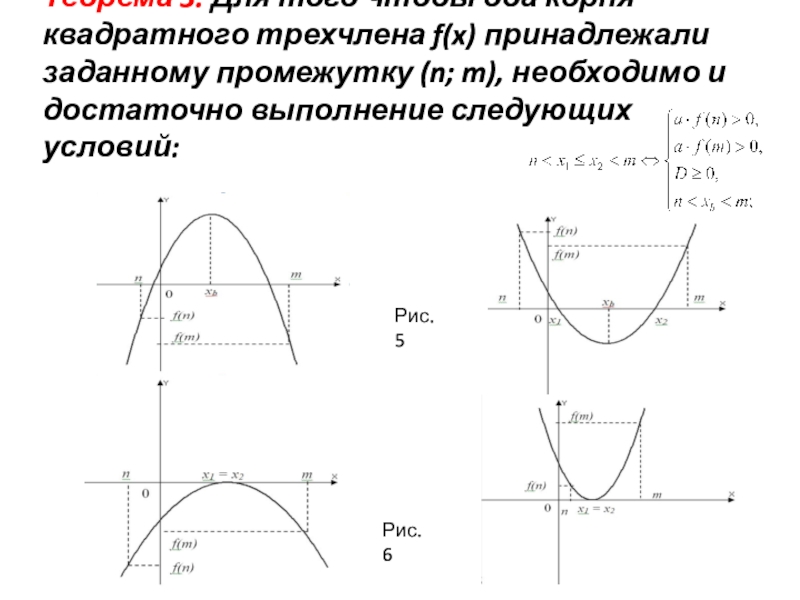
- 11. Теорема 3. Для того чтобы оба корня
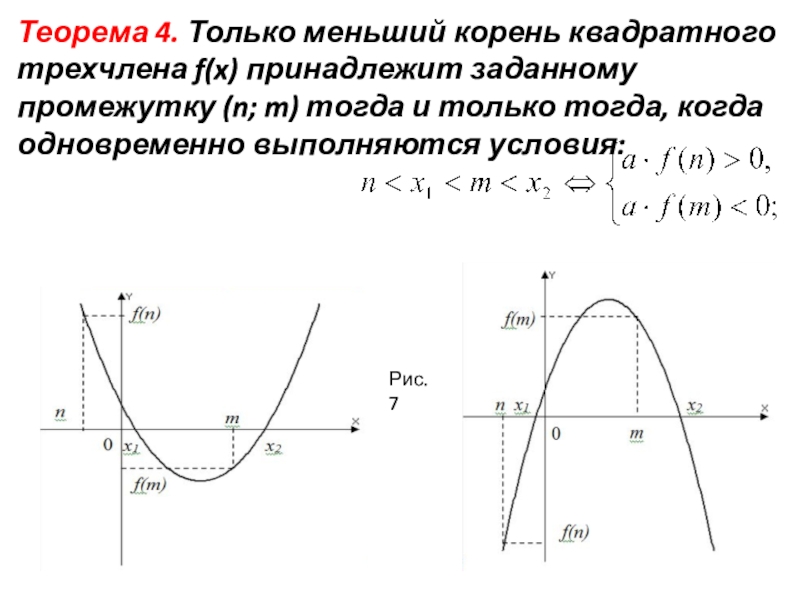
- 12. Теорема 4. Только меньший корень квадратного трехчлена
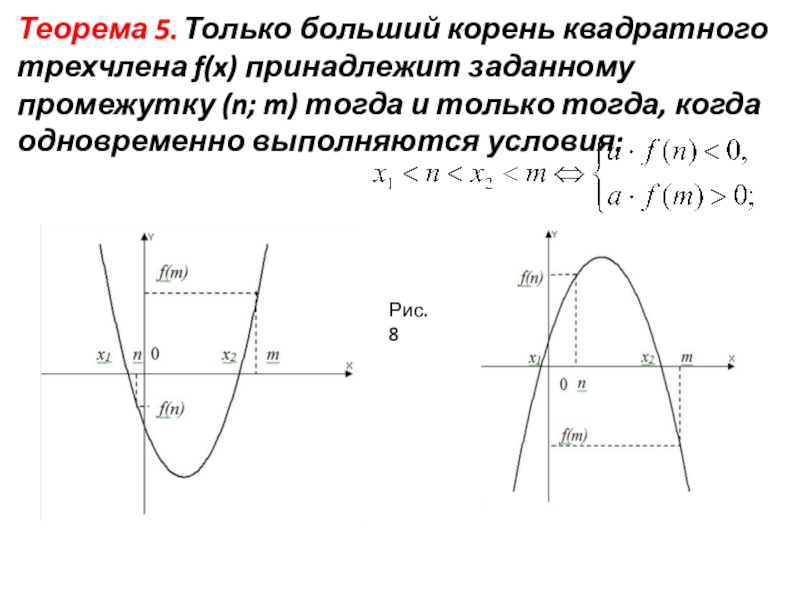
- 13. Рис. 8Теорема 5. Только больший корень квадратного
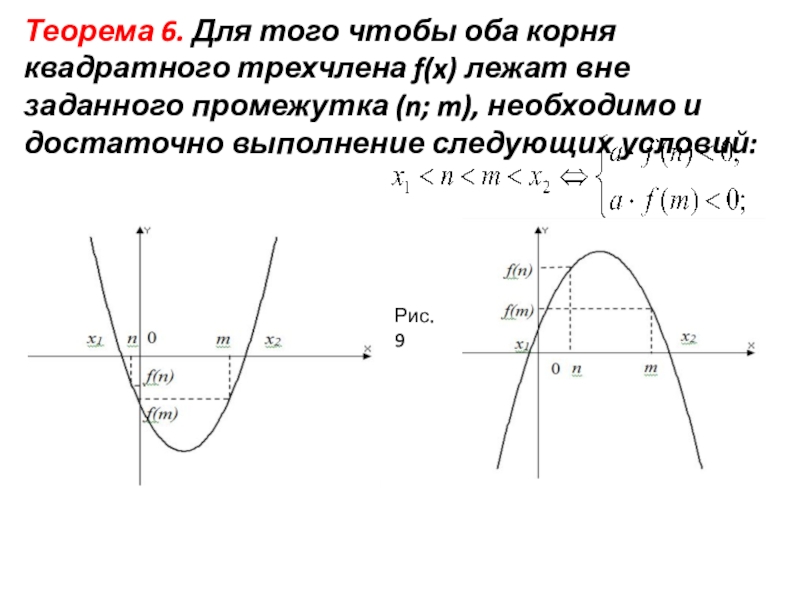
- 14. Рис. 9Теорема 6. Для того чтобы оба
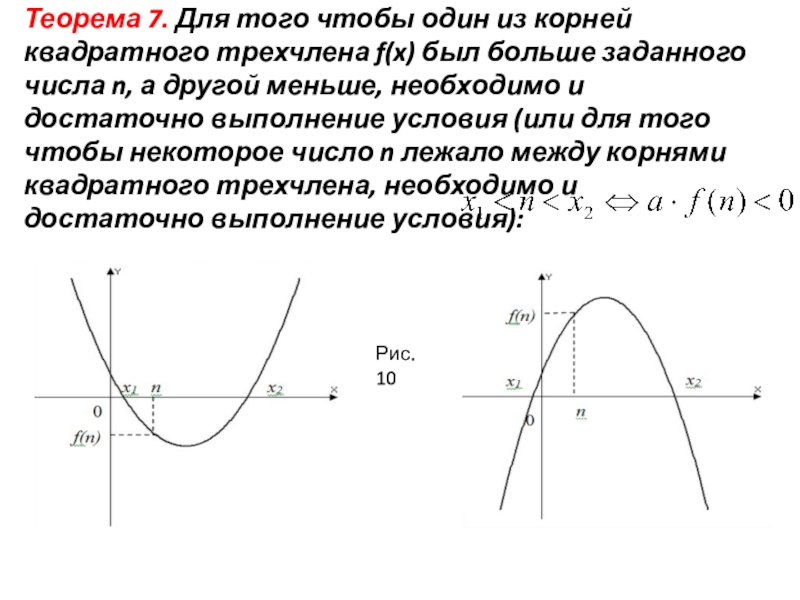
- 15. Рис. 10Теорема 7. Для того чтобы один
- 16. Теорема 8. Квадратный трехчлен f(x) имеет один
- 17. Теорема 10. Квадратные уравнения х2 + p1x
- 18. § 2. Применение теоремы Виета Некоторые задачи
- 19. 2) имеет два действительных отрицательных корня тогда
- 20. Замечание 1. Если коэффициент при х2 содержит
- 21. §3. Примеры решения задач для
- 22. Пример 4. При каких значениях параметра а
- 23. Пример 6. При каких значениях параметра а
- 24. Выводы и заключение В результате исследовательской
- 25. Решение поставленных задач убедило нас о правильности
- 26. Список использованной и рекомендуемой литературы1.Вавилов, В.В., Мельников
Слайд 1
Всероссийский конкурс научно-исследовательских работ учащихся
«Научный потенциал – XXI»
КВАДРАТНЫЕ УРАВНЕНИЯ
С ПАРАМЕТРАМИ
(исследовательская
Слайд 2квадратные уравнения с параметрами
Цель работы:
исследовать необходимые и достаточные условия расположения корней
Задачи исследовательской работы:
систематизировать теоремы о расположении корней квадратного уравнения относительно заданных точек; составить геометрические интерпретации теорем о расположении корней квадратного уравнения; доказать теорем №1, 7, 10; исследовать применение теоремы Виета к решению квадратных уравнений с параметрами; разработать общую схему исследования задач, связанных с расположением корней квадратного уравнения.
Слайд 3
Полученные данные, выводы:
В результате исследовательской работы мы изучили и систематизировали
Слайд 4План исследований
Объект исследования: квадратные уравнения с параметрами.
Предмет исследования: основные теоремы о
Гипотеза исследования: изучение теорем о расположении корней квадратного трехчлена развивает математические способности и позволит в дальнейшем овладеть приемами и способами решения более сложных задач с параметрами, тем самым обеспечит качественную подготовку к ОГЭ и ЕГЭ.
Первый этап исследований:
1.Исследование расположение корней квадратного уравнения относительно заданных точек;
2.Изучение и систематизация необходимых и достаточных условий расположение корней квадратного уравнения относительно заданных точек;
Второй этап исследований:
1.Исследование применения теоремы Виета к решению квадратных уравнений с параметрами.
Третий этап исследований:
1.Составление оптимальной и наиболее эффективной схемы исследования задач, связанных с расположением корней квадратного трехчлена f(x) = ax2 + bx + c.
Четвертый этап исследований:
1.Анализ решений квадратных уравнений с параметрами с методическими рекомендациями.
Пятый этап исследований:
1. Выводы и заключение.
Шестой этап:
1.Написание научной статьи.
Седьмой этап:
1.Составление презентации в PowerPoint
Слайд 5Оглавление
Введение
1.Обзор литературы
1.1.Теоремы о расположении корней квадратного уравнения
1.2.Теорема Виета
2.Методы исследования.
2.1.Методы исследования, используемые в работе:
2.2.План исследований
3.Результаты и обсуждение
3.1.Геометрическая иллюстрация и доказательство теорем
3.2.Следствия из теоремы Виета
3.3. Общая схема решения задач, связанных с расположением корней квадратного уравнения
3.4. Примеры решения задач для подготовки к ОГЭ и ЕГЭ по математике
4.Выводы
Список использованной и рекомендованной литературы
Слайд 6Введение
Исследовательская работа посвящена одному из наиболее трудных разделов элементарной математики: задачам
Анализ вариантов ЕГЭ и ОГЭ по математике и вступительных экзаменов в различные вузы показывает, что большинство предлагаемых задач с параметрами связано с расположением корней квадратного трехчлена. Будучи основной в школьном курсе математики, квадратичная функция формирует обширный класс задач с параметрами, разнообразных по форме и содержанию, но объединенных общей идеей – в основе их решения лежат свойства квадратичной функции. При решении задач с параметрами, в которых фигурирует квадратный трехчлен рекомендуется работать с тремя типами моделей:
вербальная модель – словесное описание задачи;
геометрическая модель – эскиз графика квадратичной функции;
аналитическая модель – система неравенств, при помощи которой описывается привести примеры решения квадратных уравнений с параметрами с подробными методическими рекомендациями.
Слайд 7 §1. Теоремы о расположении корней квадратного трехчлена
Теоремы о расположении корней
Введем следующие обозначения: х1, х2 – корни квадратного трехчлена f(x), х1 ≤ х2, D – дискриминант f(x), xb – абсцисса вершины параболы, являющейся графиком f(x). Решение большинства задач с параметром, в которых необходимо провести исследование квадратного трехчлена, сводится к определению необходимых и достаточных условий реализации одного или нескольких из следующих случаев:
Теорема 1.
Для того чтобы оба корня квадратного трехчлена f(x) = ax2 + bx + c (a ≠ 0) были больше некоторого числа n, необходимо и достаточно выполнение следующих условий:
Слайд 8Геометрическая интерпретация. Для того чтобы парабола (см. рис. 1, 2) –
Рис. 1
Рис. 2
Слайд 9Доказательство теоремы 1.
Достаточность. Так как D ≥ 0,то по теореме о
f(n) = a∙(n – x1)∙(n – x2).
Сравнение знаков левой и правой частей этого неравенства приводит нас к выводу, что выполнено неравенство n – х1<0, т.е. х1>n.
Необходимость. Так как трехчлен имеет два корня, то по теореме о дискриминанте, D≥0. Так как х1> n и х2> n, то х1+х2 > 2n, поэтому
хв = > = n.
По теореме о разложении на линейные множители, с учетом известных по условию знаков, получим запись f(n) = a∙(n – x1)∙(n – x2), из которой следует, что f(n) > 0. Тем самым теорема доказана полностью.
Слайд 10Теорема 2. Для того чтобы оба корня квадратного трехчлена f(х) были
Рис. 3
Рис. 4
Слайд 11Теорема 3. Для того чтобы оба корня квадратного трехчлена f(x) принадлежали
Рис. 5
Рис. 6
Слайд 12Теорема 4. Только меньший корень квадратного трехчлена f(x) принадлежит заданному промежутку
Рис. 7
Слайд 13Рис. 8
Теорема 5. Только больший корень квадратного трехчлена f(x) принадлежит заданному
Слайд 14Рис. 9
Теорема 6. Для того чтобы оба корня квадратного трехчлена f(x)
Слайд 15Рис. 10
Теорема 7. Для того чтобы один из корней квадратного трехчлена
Слайд 16Теорема 8. Квадратный трехчлен f(x) имеет один корень внутри интервала (n;m),
Слайд 17Теорема 10. Квадратные уравнения х2 + p1x + q1 = 0
Доказательство.
Пусть f1(x) = x2 + p1x + q1, f2(x) = x2 + p2x + q2 и числа х1, х2 являются корнями уравнения f1(x) = 0. Для того чтобы уравнения f1(x) = 0 и f2(x) = 0 имели по крайней мере один общий корень, необходимо и достаточно, чтобы f1(x)∙f2(x) = 0, т. е. чтобы (x12 + p2x1 + q2)(x22 + p2x2 + q2) = 0. Представим последнее равенство в виде
(x12 + p1x1 + q1 + (p2 – p1)x1 + q2 – q1) (x22 + p1x2 + q1 + (p2 – p1)x2 + q2 – q1) = 0.
Поскольку х12 + p1x1 + q1 = 0 и x22 + p1x2 + q1 = 0, отсюда получаем
((p2 – p1)x1 + (q2 – q1))((p2 – p1)x2 + (q2 – q1)) = 0, т. е.
(p2 – p1)2x1x2 + (q2 – q1)(p2 – p1)(x1 + x2) + (q2 – q1)2 = 0.
По теореме Виета x1 +x2 = -p1 и x1x2 =q1; следовательно,
(p2 – p1)2q1 – (q2 – q1)(p2 - p1)p1 + (q2 – q1)2 = 0, или
(q2 – q1)2 = (p2 - p1)( (q2 – q1)p1 - (p2 - p1)q1) = (p2 – p1)(q2p1 – q1p1 – p2q1 + p1q1) =
(p2 – p1)(q2p1 – p2q1), что и требовалось доказать.
Слайд 18§ 2. Применение теоремы Виета
Некоторые задачи на исследование квадратного трехчлена решаются
если х1, х2 – корни квадратного уравнения
aх2 + bх + c = 0, a≠0, то
Квадратное уравнение ax2 + bx + c = 0:
1) имеет два действительных положительных корня тогда и только тогда, когда одновременно выполняются условия:
Слайд 192) имеет два действительных отрицательных корня тогда и только тогда, когда
3) имеет два действительных корня разных знаков тогда и только тогда, когда одновременно выполняются условия:
;
4) имеет два действительных корня одного знака, если
Слайд 20Замечание 1. Если коэффициент при х2 содержит параметр, необходимо разбирать случай,
Замечание 2. Если дискриминант квадратного уравнения является полным квадратом, то вначале удобней найти явные выражения для его корней.
Замечание 3. Если уравнение, содержащее несколько неизвестных, является квадратным относительно одной из них, то часто ключом к решению задачи служит исследование его дискриминанта.
Составим схему исследования задач, связанных с расположением корней квадратного трехчлена f(x) = ax2 + bx + c:
1.Исследование случая а = о (если первый коэффициент зависит от параметров).
2.Нахождение дискриминанта D (а≠0).
3.Если D - полный квадрат некоторого выражения, то нахождение корней х1, х2 и подчинение условиям задачи.
4.Если не извлекается, то графический анализ задачи (геометрическая модель).
5.Аналитическое описание подходящих случаев расположения параболы, для чего учитываются: знак коэффициента при х, значение и знак дискриминанта, значения и знаки квадратичной функции в изучаемых точках, расположение вершины параболы относительно изучаемых точек (аналитическая модель).
6.Объединение получаемых неравенств и составление системы или систем неравенств,
7.Решение полученных систем.
Слайд 21 §3. Примеры решения задач для подготовки к ОГЭ и ЕГЭ
Пример 3. Найти все значения а, для которых уравнение
х2 – 2(а – 1)х + (2а + 1) = 0 имеет два положительных корня.
Решение. Из теоремы Виета для того чтобы оба корня х1 и х2 данного уравнения были положительными, необходимо и достаточно, чтобы дискриминант квадратного трехчлена х2 – 2(а – 1)х + (2а + 1) был неотрицательным, а произведение х1∙х2 и сумма х1 + х2 были положительными. Получаем, что все а, удовлетворяющие системе
И только они, являются решениями поставленной задачи. Э та система равносильна системе
Решением которой , а следовательно, и самой задачи являются все числа из промежутка [4; + ∞).
Слайд 22Пример 4. При каких значениях параметра а уравнение (а - 2)х2
имеет два корня, один из которых меньше 2, а другой больше 3?
Решение. По теореме 6, для того чтобы оба корня данного квадратного трехчлена лежали вне заданного промежутка, необходимо и достаточно выполнение условий
Получим систему неравенств:
Ответ: .
Слайд 23Пример 6. При каких значениях параметра а квадратное уравнение
(а – 1)х2
Решение. Согласно теореме 9, квадратный трехчлен f(x) = (a-1)x2 – 2ax + 3a – 1 имеет два корня, расположенные по одному на каждом из промежутков (0; 1) и (2; 4), если выполняются условия
то есть
< а < 1;
Ответ:
Слайд 24Выводы и заключение
В результате исследовательской работы по выбранной теме мы решили
Анализ вариантов ЕГЭ и ОГЭ по математике и вступительных экзаменов в различные вузы показывает, что большинство предлагаемых задач с параметрами связано с расположением корней квадратного трехчлена. Будучи основной в школьном курсе математики, квадратичная функция формирует обширный класс задач с параметрами, разнообразных по форме и содержанию, но объединенных общей идеей – в основе их решения лежат свойства квадратичной функции. Мы пришли к выводу, что при решении задач с параметрами, в которых фигурирует квадратный трехчлен. рекомендуется работать с тремя типами моделей:
вербальная модель – словесное описание задачи;
геометрическая модель – эскиз графика квадратичной функции;
аналитическая модель – система неравенств, составленная на основе теорем о расположении корней квадратного трехчлена и теоремы Виета, при помощи которой описывается геометрическая модель.
Слайд 25Решение поставленных задач убедило нас о правильности выдвинутой в начале работы
Мы убедились в том, что огромную роль играют задачи с параметрами, в которых фигурирует квадратный трехчлен в формировании логического мышления, математической культуры, развития исследовательских навыков. В процессе работы над данным проектом у нас повысился интерес к предмету, ориентация на подготовку продолжения образования по избранному предмету. Поэтому, владея методами решения задач с параметрами можно успешно справиться и с другими задачами. Наша творческая и исследовательская работа по данной теме помогла нам в подготовке к ОГЭ, мы научились решать задания с параметрами, входящие в КИМы ОГЭ (задание №23) и ЕГЭ (задание С5 –задание 18).
Слайд 26Список использованной и рекомендуемой литературы
1.Вавилов, В.В., Мельников И.И., Олехник С.Н., Пасиченко
2.Вавилов В.В., Мельников И.И., Олехник С.Н., Пасиченко П.И. Задачи по математике. Уравнения и неравенства./ В.В.Вавилов, И.И.Мельников, С.Н.Олехник, П.И.Пасиченко// М.: «Наука», 1988. – 240 с.
3.Горштейн П.И., Полонский В.Б.,Якир М.С. Задачи с параметрами/П.И. Горштейн, В.Б. Полонский, М.С. Якир// М.:«Илекса», Харьков.:«Гимназия», 2002. – 336 с.
4.Дорофеев Г.В., Потапов М.К., Розов Н.Х. Пособие по математике для поступающих в вузы./ Г.В.Дорофеев., М.К.Потапов., Н.Х.Розов//Москва. «Наука», 1976.
5.Жаржевский А.Я., Фельдман Я.С. Решение задач с параметрами/ А.Я. Жаржевский, Я.С. Фельдман// Санкт-Петербург. «Агентство ИГРЕК», 1996.
6.Звавич Л.И., Шляпочник Л.Я., Чинкина М.В. Алгебра и начала анализа 8-11. Пособие для школ и классов с углубленным изучением математики/ Л.И. Звавич , Л.Я. Шляпочник, М.В. Чинкина//«Дрофа», Москва, 2001.
7.Козко А.И., Чирский В.Г.. Задачи с параметрами и другие сложные задачи/ А.И. Козко, В.Г. Чирский// М.: МЦНОМО, 2007, - 296 стр.
8.Никольская И.Л. Факультативный курс по математике 7-9 классы/ И.Л. Никольская// Москва, «Просвещение»,1991. – 383с.
9.Прокофьев А.А. Задачи с параметрами/ А.А. Прокофьев// М.:МИЭТ,2004, - 258С.
10.Рязановский А.Р. 500 способов и методов решения задач по математике для школьников и поступающих в вузы/ А.Р. Рязановский//Москва, «Дрофа», 2001. – 480 с.
11.Черкасов О.Ю., Якушев А.Г. Математика: Справочник для старшеклассников и поступающих в вузы/ О.Ю. Черкасов, А.Г. Якушев// Москва, .«АСТ – Пресс. Школа» 2002.
12.Шабунин М.И. Математика для поступающих в ВУЗы/ М.И. Шабунин// Москва, .«Аквариум», 1997. – 272 с.
13.Шарыгин И.Ф. Факультативный курс по математике: решение задач. 10 класс/ И.Ф. Шарыгин// Москва. «Просвещение»,1989. – 252с.
14.Шарыгин И.Ф., Голубев В.И.. Факультативный курс по математике. 11 класс/ И.Ф. Шарыгин, В.И. Голубев// Москва. «Просвещение», 1991. – 384с.
15.Шарыгин И.Ф. Сборник задач по математике с решениями/ И.Ф. Шарыгин//Москва, «Астрель», 2001. – 400 с.