- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Многогранники вокруг нас
Содержание
- 1. Презентация Многогранники вокруг нас
- 2. Цель:рассмотреть виды правильных многогранников и их свойства.
- 3. это поверхность составленная из многоугольников, и
- 4. Признаки правильных многогранников:
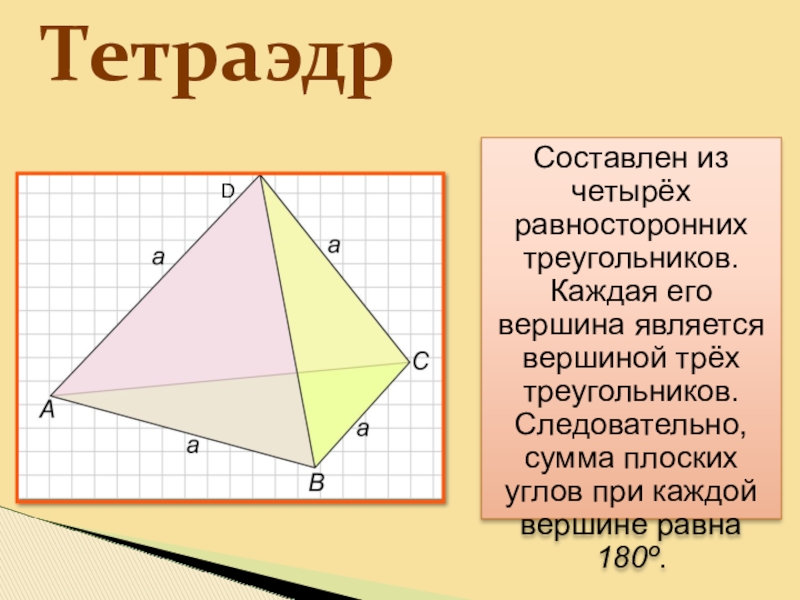
- 5. Составлен из четырёх равносторонних треугольников. Каждая его
- 6. Куб или ГексаэдрСоставлен из шести квадратов. Каждая
- 7. ОКТАЭДРСоставлен из восьми равносторонних треугольников. Каждая вершина
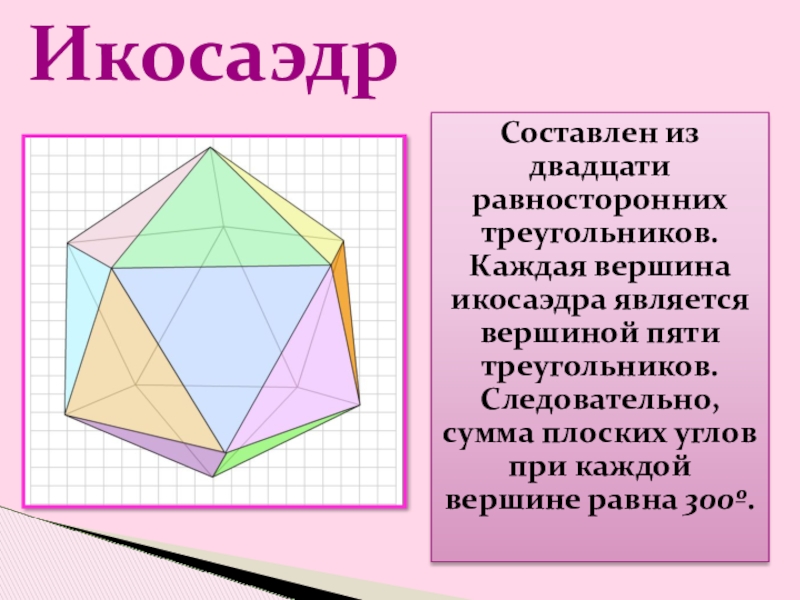
- 8. Составлен из двадцати равносторонних треугольников. Каждая вершина
- 9. Составлен из двенадцати правильных пятиугольников. Каждая вершина
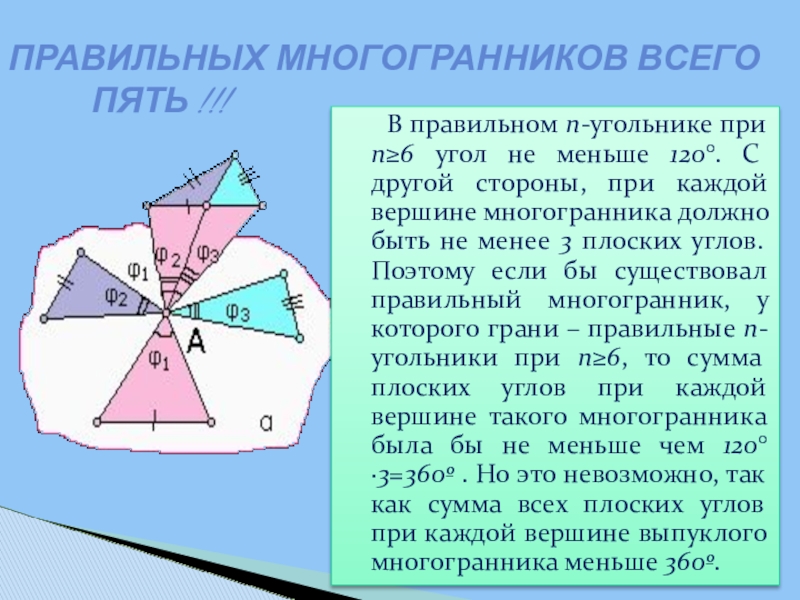
- 10. В правильном n-угольнике при
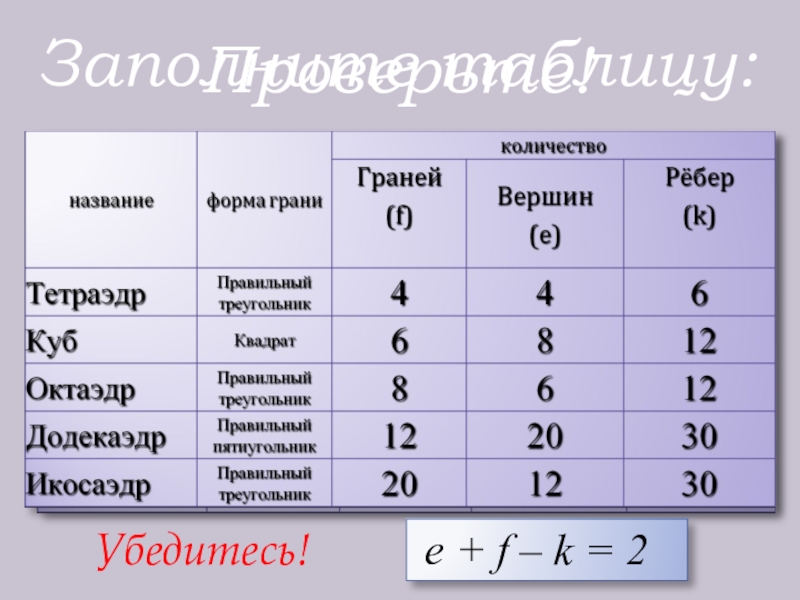
- 11. Заполните таблицу:Проверьте! e + f – k = 2Убедитесь!
- 12. Теорема Эйлера e + f –
- 13. рассмотрим влияние правильных многогранников на возникновение философских теорий и гипотез.
- 14. В своих философских теориях правильные многогранники использовали:ПлатонПифагорЕвклидАрхимедКеплер
- 15. Древнегреческий ученый и философ Платон считал, что
- 16. Виды
- 17. Пифагорейцы уделяли в своих космологических теориях особенно
- 18. Космологическая гипотеза Кеплера
- 19. Связь многогранников с природой.
- 20. В книге немецкого биолога Э. Геккеля "Красота
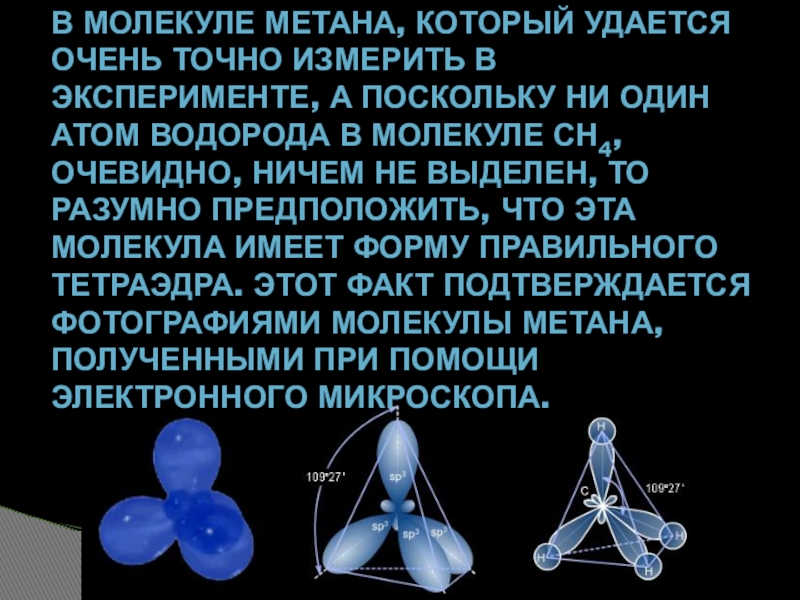
- 21. В МОЛЕКУЛЕ МЕТАНА, КОТОРЫЙ УДАЕТСЯ ОЧЕНЬ ТОЧНО
- 22. Простейшее животное Большинство феодарий живут на
- 23. Вирус не может быть совершенно круглым, как
- 24. Чудо природы – кристаллыПравильные многогранники -
- 25. Примеры применения многогранников в архитектуре
- 26. «Математика владеет не только истиной,
- 27. Слайд 27
- 28. Многогранники нашли широкое применение в архитектуре. Современные
Слайд 3 это поверхность составленная из многоугольников, и ограничивающая некоторое геометрическое тело.
Многогранник-
Многогранник,
правильным.
Слайд 5Составлен из четырёх равносторонних треугольников. Каждая его вершина является вершиной трёх
Тетраэдр
D
Слайд 6Куб или Гексаэдр
Составлен из шести квадратов. Каждая вершина куба является вершиной
Слайд 7ОКТАЭДР
Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх
Слайд 8Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти
Икосаэдр
Слайд 9Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх
Додекаэдр
Слайд 10 В правильном n-угольнике при n≥6 угол не меньше
ПРАВИЛЬНЫХ МНОГОГРАННИКОВ ВСЕГО
ПЯТЬ !!!
Слайд 12Теорема Эйлера
e + f – k = 2
Где
f – число граней,
k – число ребер
Эйлерова характеристика всякого многогранника нулевого рода равна 2. Иначе говоря, между e, f и k любого многогранника нулевого рода имеет место зависимость .
Слайд 14 В своих философских теориях
Платон
Пифагор
Евклид
Архимед
Кеплер
Слайд 15Древнегреческий ученый и философ Платон считал, что эти тела олицетворяют сущность
(IV–V в до н. э.)
Слайд 17Пифагорейцы уделяли в своих космологических теориях особенно важное место правильным многогранникам,
Правильными многогранниками занимался Архимед. Ему также принадлежит открытие тринадцати так называемых полуправильных многогранников («архимедовых тел»).
Учение о правильных многогранниках, содержащееся в последней XIII книге Евклида, является венцом его «Начал».
Слайд 18Космологическая гипотеза Кеплера
Кеплер попытался связать со свойствами правильных многогранников некоторые свойства Солнечной системы.
Он предположил, что расстояния между шестью известными тогда планетами выражаются через размеры пяти правильных выпуклых многогранников .
Вокруг сферы Меркурия, ближайшей к Солнцу планеты, описан октаэдр
Этот октаэдр вписан в сферу Венеры, вокруг которой описан икосаэдр.
Вокруг икосаэдра описана сфера Земли, а вокруг этой сферы - додекаэдр.
Додекаэдр вписан в сферу Марса, вокруг которой описан тетраэдр
Вокруг тетраэдра описана сфера Юпитера, вписанная в куб.
Наконец, вокруг куба описана сфера Сатурна.
Слайд 20В книге немецкого биолога Э. Геккеля "Красота форм в природе"
можно
"Природа вскармливает на своем лоне неисчерпаемое количество удивительных созданий, которые по красоте и разнообразию далеко превосходят все созданные искусством человека формы".
Слайд 21В МОЛЕКУЛЕ МЕТАНА, КОТОРЫЙ УДАЕТСЯ ОЧЕНЬ ТОЧНО ИЗМЕРИТЬ В ЭКСПЕРИМЕНТЕ, А
Слайд 22Простейшее животное
Большинство феодарий живут на морской глубине и служат
Из всех многогранников с тем же числом граней икосаэдр имеет наибольший объём при наименьшей площади поверхности.
Это свойство помогает морскому организму преодолевать давление толщи воды.
Феодария
по форме напоминает икосаэдр
Слайд 23Вирус не может быть совершенно круглым, как считалось ранее. Чтобы установить
ИНТЕРЕСНО!
Икосаэдр оказался в центре внимания биологов, в их спорах относительно формы вирусов.
вирус полиомиелита
Слайд 24 Чудо природы – кристаллы
Правильные многогранники - самые выгодные фигуры. И
кристаллы поваренной соли NaCl
фосфорноватистая кислота (Н3РО2)
Слайд 26 «Математика владеет не только истиной, но и высшей красотой
Бертран Рассел
Свято-Преображенский кафедральный собор.
Успенский собор