- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Многогранники вокруг нас
Содержание
- 1. Презентация Многогранники вокруг нас
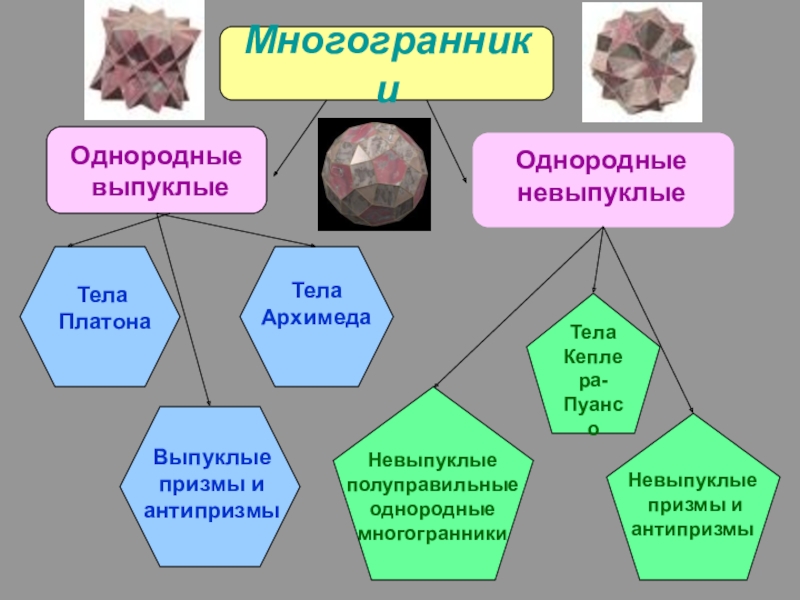
- 2. МногогранникиОднородные выпуклыеОднородные
- 3. Правильными многогранниками называют выпуклые многогранники, все грани
- 4. Правильные многогранники Тетраэдр -правильная треугольная пирамида с равными ребрами, ограниченная четырьмя правильными треугольниками.
- 5. Правильные многогранники Октаэдр – правильный четырёхугольный диэдр с равными рёбрами, ограниченный восемью правильными треугольниками.
- 6. Икосаэдр- поверхность, ограниченная двадцатью правильными треугольниками.Правильные многогранники
- 7. Куб(гексаэдр)- правильная четырёхугольная призма с равными рёбрами, ограниченная шестью квадратами.Правильные многогранники
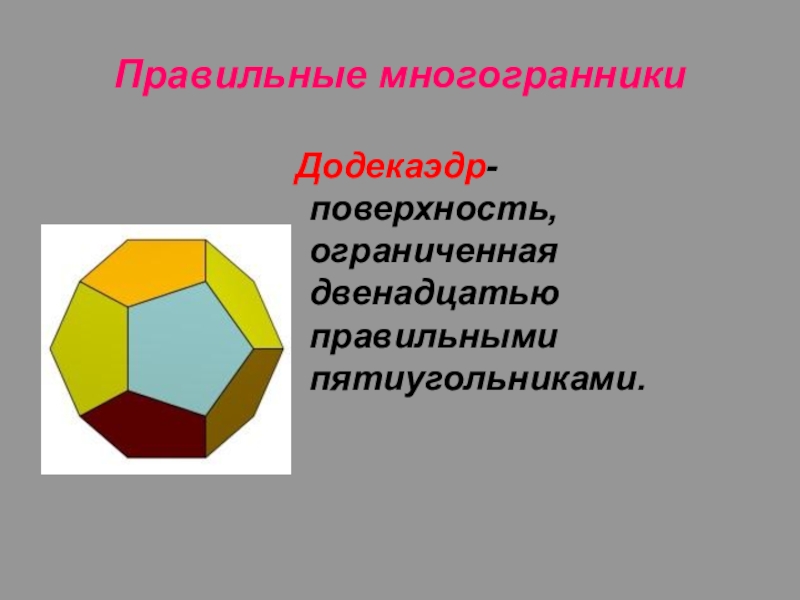
- 8. Правильные многогранники Додекаэдр- поверхность, ограниченная двенадцатью правильными пятиугольниками.
- 9. Сделаем вывод:Мы убедились, что существует лишь пять
- 10. ТетраэдрИкосаэдрГексаэдрДодекаэдрОктаэдр
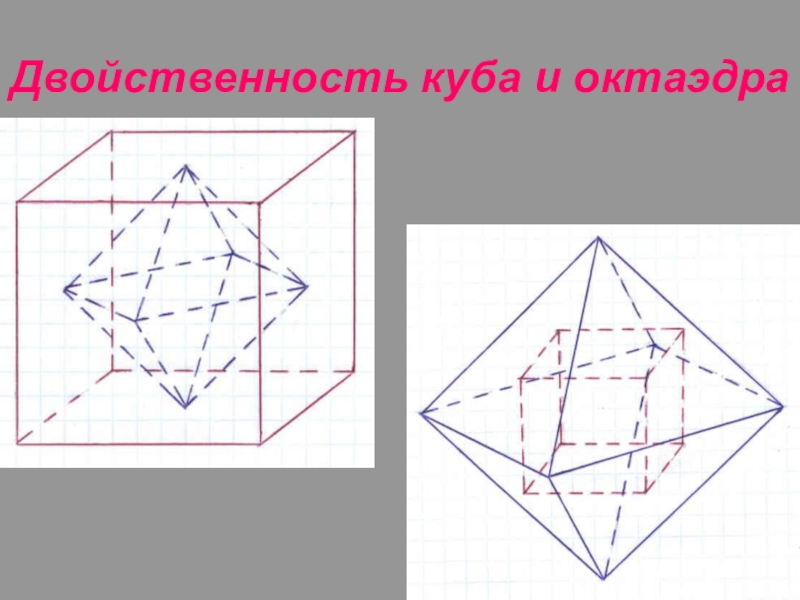
- 11. Двойственность куба и октаэдра
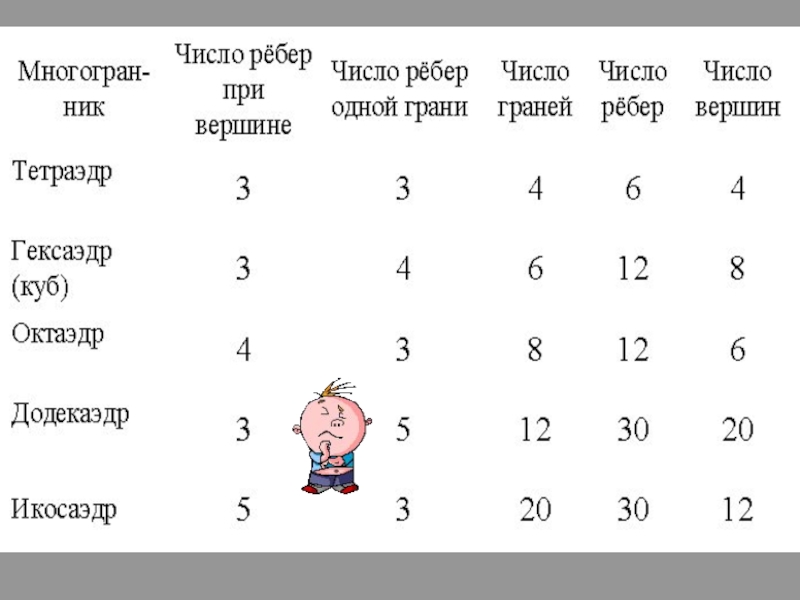
- 12. Число вершин минус число ребер плюс число
- 13. Слайд 13
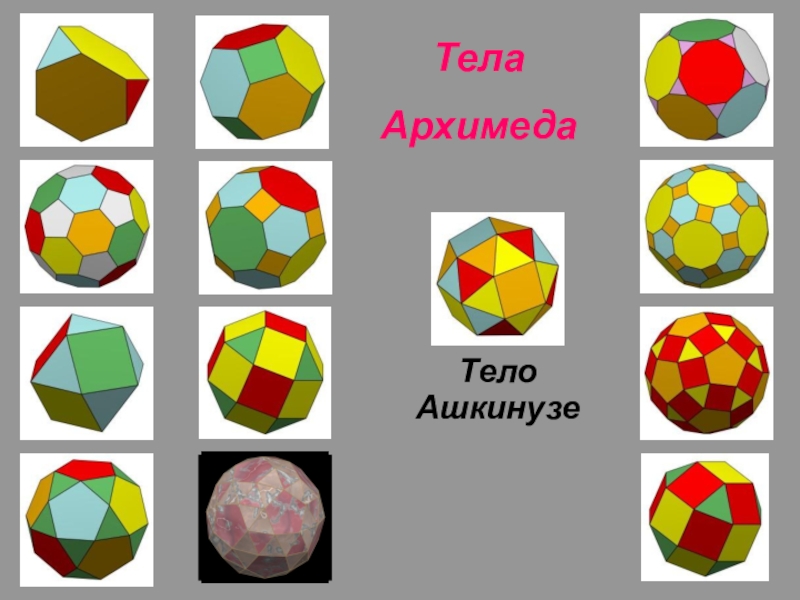
- 14. Тела АрхимедаАрхимедовыми телами называются полуправильные однородные выпуклые
- 15. Тела АрхимедаТелоАшкинузе
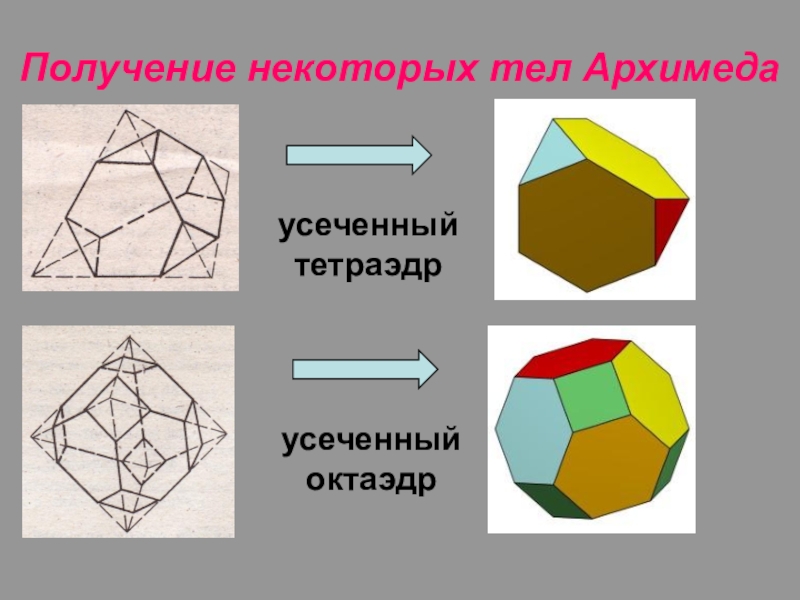
- 16. Получение некоторых тел Архимедаусеченный тетраэдрусеченный октаэдр
- 17. Тела Кеплера – Пуансо (правильные звездчатые многогранники)
- 18. Большой звездчатыйдодекаэдрБольшой икосаэдрМалый звездчатыйдодекаэдрБольшой додекаэдр
- 19. Получение тел Кеплера - ПуансоПродолжение рёбер додекаэдра
- 20. Многогранники в природе
- 21. Многогранники в ювелирном деле
- 22. Многогранники в архитектуре
Слайд 2Многогранники
Однородные
выпуклые
Однородные
Тела
Архимеда
Тела
Платона
Выпуклые
призмы и
антипризмы
Тела
Кеплера-
Пуансо
Невыпуклые
полуправильные
однородные
многогранники
Невыпуклые
призмы и
антипризмы
Слайд 3Правильными многогранниками
называют выпуклые многогранники, все грани и все углы которых
В каждой вершине правильного многогранника сходится одно и то же число рёбер.
Все двугранные углы при рёбрах и все многогранные углы при вершинах правильного многоугольника равны.
Правильные многогранники - трёхмерный аналог плоских правильных многоугольников.
Слайд 4Правильные многогранники
Тетраэдр -правильная треугольная пирамида с равными ребрами, ограниченная
Слайд 5Правильные многогранники
Октаэдр – правильный четырёхугольный диэдр с равными рёбрами, ограниченный
Слайд 6 Икосаэдр- поверхность, ограниченная двадцатью правильными треугольниками.
Правильные многогранники
Слайд 7
Куб(гексаэдр)- правильная четырёхугольная призма с равными рёбрами, ограниченная шестью
Правильные многогранники
Слайд 8Правильные многогранники
Додекаэдр- поверхность, ограниченная двенадцатью правильными пятиугольниками.
Слайд 9Сделаем вывод:
Мы убедились, что существует лишь пять выпуклых правильных многогранников -
Эти тела еще называют
телами Платона.
Слайд 14Тела Архимеда
Архимедовыми телами называются полуправильные однородные выпуклые многогранники, то есть выпуклые
Слайд 19Получение тел Кеплера - Пуансо
Продолжение рёбер додекаэдра приводит к замене каждой
На продолжении граней додекаэдра возможны следующие два случая:
если рассматривать правильные пятиугольники, то получается большой додекаэдр;
если же в качестве граней рассматривать звёздчатые пятиугольники, то получается большой звёздчатый додекаэдр.
При продолжении граней правильного икосаэдра получается большой икосаэдр.