Н.И.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Международный день числа Пи
Содержание
- 1. Презентация Международный день числа Пи
- 2. Слайд 2
- 3. Число π — математическая константа, выражающая отношение
- 4. Свое обозначение число π обрело сложным путем:
- 5. Три периода в истории числа: древний период
- 6. Слайд 6
- 7. Клавдий Птолемей (II век н. э.) π = 377/120 =
- 8. ...Приближение π = 22/7 определил древнегреческий математик Архимед. В
- 9. Слайд 9
- 10. Эпоха цифровой техники в XX веке привела к увеличению
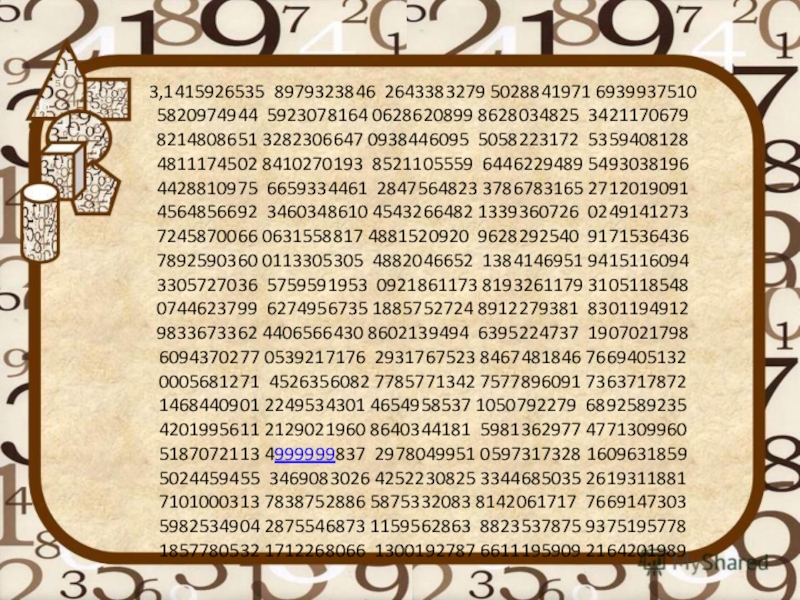
- 11. 3,1415926535 8979323846 2643383279 5028841971 6939937510
- 12. Для запоминания числа "Пи" было придумано двустишие.
- 13. Краткая сводка рекордной погони за «хвостом» числа Пи выглядит
- 14. Слайд 14
- 15. Памятник числу Пи перед зданием Музея искусств в Сиэтле
- 16. Слайд 16
- 17. π - поистине уникальное число1. Ученые считают,
- 18. Отношение длины основания Пирамиды Хеопса к ее
- 19. Викторина Когда отмечают международный день числа π?С
- 20. Спасибо за внимание
Число π — математическая константа, выражающая отношение длины окружности к длине ее диаметра. В цифровом выражении π начинается как 3,141592... и имеет бесконечную математическую продолжительностьПрактическое задание.1.Начертите окружность любого радиуса. С помощью нитки и линейки измерьте длину
Слайд 3Число π — математическая константа, выражающая отношение длины окружности к длине
ее диаметра. В цифровом выражении π начинается как 3,141592... и имеет бесконечную математическую продолжительность
Практическое задание.
1.Начертите окружность любого радиуса. С помощью нитки и линейки измерьте длину окружности. Измерьте длину диаметра. Найдите отношение длины окружности к её диаметру.
2. Длина экватора Земли равна 40075 км, радиус Земли равен 6378 км. Найдите отношение длины экватора к диаметру Земли.
Слайд 4Свое обозначение число π обрело сложным путем: сначала этой греческой буквой
в 1647 году математик Оутрейд обозвал длину окружности. Он взял первую букву греческого слова περιφέρεια — «переферия», «окружность». В 1706 году английский преподаватель Уильям Джонс в работе «Обозрение достижений математики» уже называл буквой π отношение длины окружности к ее диаметру. А закрепил название математик XVIII века Леонард Эйлер, перед авторитетом которого остальные склонили головы.
Слайд 5Три периода в истории числа:
древний период
(число π изучалось с
позиции геометрии)
2. классическая эра
(развитие математического анализа в Европе в XVII веке)
3. эра цифровых компьютеров
2. классическая эра
(развитие математического анализа в Европе в XVII веке)
3. эра цифровых компьютеров
Слайд 7Клавдий Птолемей (II век н. э.)
π = 377/120 = 3, 14166667..
Цзу Чунчжи (V век
н. э.)
π = 355/113 = 3, 14159292 ..
π = 355/113 = 3, 14159292 ..
Слайд 8...
Приближение π = 22/7 определил древнегреческий математик Архимед. В честь этого часто такое
приближение называют "Архимедовым" числом. Архимеду удалось не только установить приближенное значение для π, но также найти точность этого приближения, а именно – найти узкий числовой промежуток, которому принадлежит значение π. В одной из своих работ Архимед доказывает цепь неравенств, которая на современный лад выглядела бы так:
3,140 909 < π < 3,1 428 265...
Как видим из неравенства, Архимед нашел довольно-таки точное значение с точностью до 0,002. Самое удивительно то, что он нашел два первых знака после запятой: 3,14...
3,140 909 < π < 3,1 428 265...
Как видим из неравенства, Архимед нашел довольно-таки точное значение с точностью до 0,002. Самое удивительно то, что он нашел два первых знака после запятой: 3,14...
Слайд 9 Используя метод Архимеда,
можно вычислить π с любой точностью.
В XV веке в «Трактате об окружности» Джамшид аль-Каши вычислил длину окружности по рецепту Архимеда — как среднее арифметическое между периметрами вписанного и описанного правильных многоугольников с числом сторон 3 · 228. Это дало ему для 2π приближенние 6,2831853071795865. Это значение, верное во всех 16 десятичных знаках, было получено из вычисленного им ранее в шестидесятеричной системе значения с 9 знаками. В 1596 году Людольф ван Келен из Дельфта получил 35 знаков числа π. Леонард Эйлер вычислил π с точностью до 153 десятичных знаков.
В XV веке в «Трактате об окружности» Джамшид аль-Каши вычислил длину окружности по рецепту Архимеда — как среднее арифметическое между периметрами вписанного и описанного правильных многоугольников с числом сторон 3 · 228. Это дало ему для 2π приближенние 6,2831853071795865. Это значение, верное во всех 16 десятичных знаках, было получено из вычисленного им ранее в шестидесятеричной системе значения с 9 знаками. В 1596 году Людольф ван Келен из Дельфта получил 35 знаков числа π. Леонард Эйлер вычислил π с точностью до 153 десятичных знаков.
Слайд 10Эпоха цифровой техники в XX веке привела к увеличению скорости появления вычислительных рекордов. Джон
фон Нейман и другие использовали в 1949 году ЭНИАК для вычисления 2037 цифр , которое заняло 70 часов. Ещё одна тысяча цифр была получена в последующие десятилетия, а отметка в миллион была пройдена в 1973 году (десяти знаков числа π, что вполне достаточно для всех практических целей). Такой прогресс имел место не только благодаря более быстрому аппаратному обеспечению, но и благодаря алгоритмам. Одним из самых значительных результатов было открытие в 1960 году быстрого преобразования Фурье, что позволило быстро осуществлять арифметические операции над очень большими числами.
В начале XX века индийский математик Сриниваса Рамануджан обнаружил множество новых формул для π, некоторые из которых стали знаменитыми из-за своей элегантности и математической глубины.
В начале XX века индийский математик Сриниваса Рамануджан обнаружил множество новых формул для π, некоторые из которых стали знаменитыми из-за своей элегантности и математической глубины.
Слайд 113,1415926535 8979323846 2643383279 5028841971 6939937510
5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989
Слайд 12Для запоминания числа "Пи" было придумано двустишие. В учебнике Л.Ф.Магницкого "Арифметика"
оно написано по правилам старой русской орфографии, по которой после согласной в конце слова обязательно ставился "мягкий" или "твердый" знак.
Кто и шутя, и скоро пожелаетъ "Пи" узнать число - ужъ знаетъ.
Например, запомнить фразу, в которой каждое слово состоит из количества букв, равных знакам числа Пи после запятой, а именно «это я знаю и помню прекрасно» (это — 3, я — 1 и т.д., — 3.14159).
Или зазубрить стих, в котором звучат знаки числа 3.1415926:
Нужно только постараться И запомнить все, как есть: Три, четырнадцать, пятнадцать, Девяносто два и шесть.
Для запоминания тринадцати знаков после запятой числа Пи необходимо запомнить:
Чтобы нам не ошибаться, Надо правильно прочесть: Три, четырнадцать, пятнадцать, Девяносто два и шесть. Ну и дальше надо знать,
Если мы вас спросим — Это будет пять, три, пять, И восемь.
Кто и шутя, и скоро пожелаетъ "Пи" узнать число - ужъ знаетъ.
Например, запомнить фразу, в которой каждое слово состоит из количества букв, равных знакам числа Пи после запятой, а именно «это я знаю и помню прекрасно» (это — 3, я — 1 и т.д., — 3.14159).
Или зазубрить стих, в котором звучат знаки числа 3.1415926:
Нужно только постараться И запомнить все, как есть: Три, четырнадцать, пятнадцать, Девяносто два и шесть.
Для запоминания тринадцати знаков после запятой числа Пи необходимо запомнить:
Чтобы нам не ошибаться, Надо правильно прочесть: Три, четырнадцать, пятнадцать, Девяносто два и шесть. Ну и дальше надо знать,
Если мы вас спросим — Это будет пять, три, пять, И восемь.
Слайд 13Краткая сводка рекордной погони за «хвостом» числа Пи выглядит так.
1995 — японец Хирюки Гото
сумел назвать по памяти 42 195 знаков после запятой.
2004 — еще один представитель Страны восходящего солнца, 59-летний Акира Харагучи, поднял эту планку до 54-тысячных.
2005 — все тот же неугомонный Акира Харагучи запомнил число Пи с точностью до 83 431 цифры после запятой.
2005 — китаец Чао Лю чуть-чуть не дотянул до рекорда своего восточного соседа: 67 890 знаков уместились в голове Лю.
Слайд 17
π - поистине уникальное число
1. Ученые считают, что количество знаков в
числе π бесконечно. Их последовательность не повторяется. Более того, найти повторения не удастся никому и никогда. Так как число бесконечно, оно может заключать в себе абсолютно все, даже симфонию Рахманинова, Ветхий Завет, ваш номер телефона и год, в котором наступит Апокалипсис.
2. π связано с теорией хаоса. К такому выводу пришли ученые после создания вычислительной программы Бэйли, которая показала, что последовательность чисел в π абсолютно случайна, что соответствует теории.
3. Вычислить число до конца практически невозможно – это заняло бы слишком много времени.
4. π – иррациональное число, то есть его значение нельзя выразить дробью.
5. π – трансцедентное число. Его нельзя получить, произведя какие-либо алгебраические действия над целыми числами.
6. Тридцать девять знаков после запятой в числе π достаточно для того, что вычислить длину окружности, опоясывающей известные космические объекты во Вселенной, с погрешностью в радиус атома водорода.
7. Число π связано с понятием «золотого сечения». В процессе измерений Великой пирамиды в Гизе археологи выяснили, что ее высота относится к длине ее основания, так же как радиус окружности - к ее длине.
2. π связано с теорией хаоса. К такому выводу пришли ученые после создания вычислительной программы Бэйли, которая показала, что последовательность чисел в π абсолютно случайна, что соответствует теории.
3. Вычислить число до конца практически невозможно – это заняло бы слишком много времени.
4. π – иррациональное число, то есть его значение нельзя выразить дробью.
5. π – трансцедентное число. Его нельзя получить, произведя какие-либо алгебраические действия над целыми числами.
6. Тридцать девять знаков после запятой в числе π достаточно для того, что вычислить длину окружности, опоясывающей известные космические объекты во Вселенной, с погрешностью в радиус атома водорода.
7. Число π связано с понятием «золотого сечения». В процессе измерений Великой пирамиды в Гизе археологи выяснили, что ее высота относится к длине ее основания, так же как радиус окружности - к ее длине.
Слайд 18Отношение длины основания Пирамиды Хеопса к ее
высоте, разделенное пополам, дает
знаменитое число π.
Возможно, оно намеренно зашифровано в размерах
Великой Пирамиды, причем сболее точным значением, чем
его знал великий Архимед, живший позже на 2000 лет.
Возможно, оно намеренно зашифровано в размерах
Великой Пирамиды, причем сболее точным значением, чем
его знал великий Архимед, живший позже на 2000 лет.
Слайд 19Викторина
Когда отмечают международный день числа π?
С какого года отмечается
праздник числа π ?
Кто из великих ученых родился в этот день?
От какого греческого слова происходит обозначение числа «пи» буквой π ?
Какой дробью представлял Архимед число π?
В какой стране установлен металлический памятник числу π?
Запишите первые несколько знаков числа π после запятой.
Является число π конечным или бесконечным, натуральным, целым, рациональным или иррациональным?
Вспомните формулы, в которые входит число π.
Кто из великих ученых родился в этот день?
От какого греческого слова происходит обозначение числа «пи» буквой π ?
Какой дробью представлял Архимед число π?
В какой стране установлен металлический памятник числу π?
Запишите первые несколько знаков числа π после запятой.
Является число π конечным или бесконечным, натуральным, целым, рациональным или иррациональным?
Вспомните формулы, в которые входит число π.