- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад математика на тему Построение графиков функций
Содержание
- 1. Презентация математика на тему Построение графиков функций
- 2. СодержаниеАктуальность темыГеометрические преобразования графиковМетод рамокМетод инверсииМетод инверсии
- 3. Рассмотрение данной темы традиционно важно для подготовки
- 4. Геометрические преобразования графиков в 8 классе (построение
- 5. параллельный перенос вдоль осей;симметрия относительно осей;модуль функции;сжатие
- 6. Метод рамокОсновная идея метода состоит:в выделении с
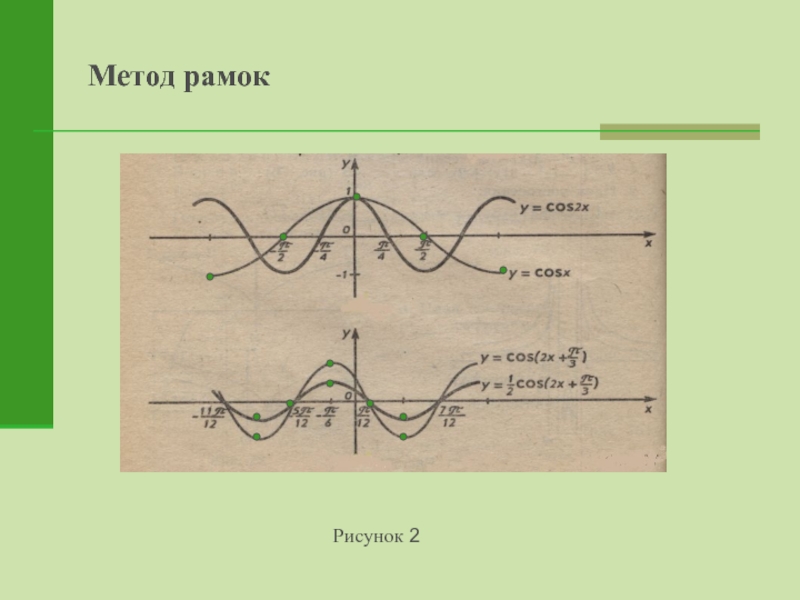
- 7. Метод рамокРисунок 2
- 8. Метод рамокПреимущества метода:метод хорошо и быстро усваивается
- 9. Метод инверсии Переход к применению инверсиизатруднителен, ибо
- 10. Метод инверсии Новая тема начинается срассмотрения графикафункции,
- 11. Метод инверсии Так как учащиеся знают, что
- 12. Метод инверсии Определение инверсии относительно прямой:
- 13. Инверсия относительно оси ОХГрафик: q ( x
- 14. Инверсия относительно оси ОУГрафик: q (x )
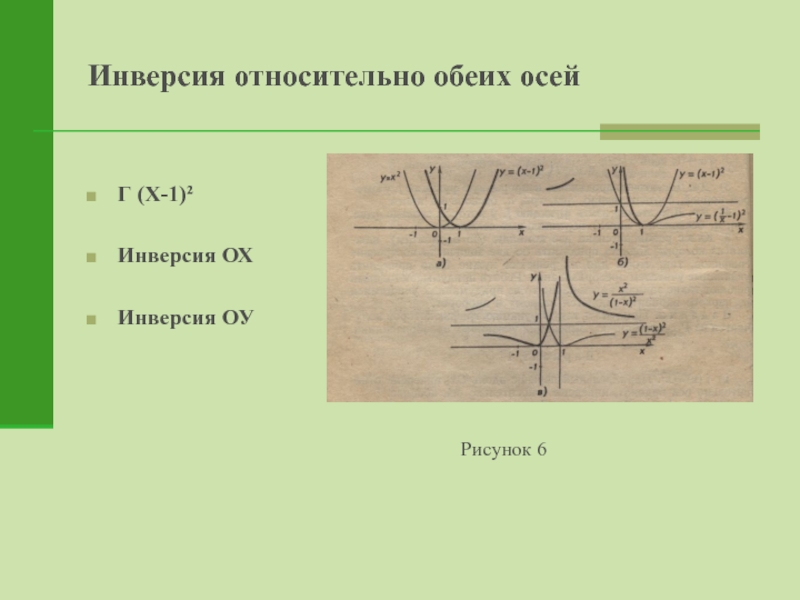
- 15. Инверсия относительно обеих осей Г (Х-1)²Инверсия ОХИнверсия ОУРисунок 6
- 16. Свойства инверсий и построение графиков с их
- 17. Свойства инверсий и построение графиков Рисунок 7
- 18. Практическое применение инверсии Рассмотренная тема
- 19. Практическое применение инверсии С помощью графика
- 20. Практическое применение инверсииРисунок 8с помощью графика легко
- 21. По данной теме проводятся: уроки-практикумыколлоквиумыпрезентации
- 22. Список используемой литературыИ.М. Гельфанд, Е.Г. Глаголева, Э.Э.
Слайд 2Содержание
Актуальность темы
Геометрические преобразования графиков
Метод рамок
Метод инверсии
Метод инверсии относительно оси ОХ
Метод инверсии
Метод инверсии относительно обеих осей
Практическое применение инверсии
Список используемой литературы
Слайд 3Рассмотрение данной темы традиционно важно для подготовки к вступительным экзаменам, при
закладываются основы аналитического мышления;
формируется интуиция;
развивается логика и культура использования функциональных обозначений и методов.
Слайд 4Геометрические преобразования графиков
в 8 классе (построение графиков с помощью параллельных
в 9 классе (с помощью сжатий и растяжений вдоль осей);
в 10 классе (повторение всех преобразований при построении графиков тригонометрических функций, функций, содержащих целую и дробную часть, построение графиков с помощью инверсий относительно осей координат, построение графиков с помощью пределов и производных).
Геометрические преобразования графиков применяются:
Слайд 5параллельный перенос вдоль осей;
симметрия относительно осей;
модуль функции;
сжатие относительно осей.
y = a f ( b x + c ) + d ,
выделить одну из последовательностей преобразований исходной функции
y = f ( x ) :
Геометрические преобразования графиков
Рисунок 1
Слайд 6Метод рамок
Основная идея метода состоит:
в выделении с помощью прямоугольной определенной части
в фиксировании на этой части графика определённых точек (контрольных): нули функции, точки экстремумов, расположение которых не меняется по отношению к рамке при преобразованиях сдвига и сжатия.
Слайд 8Метод рамок
Преимущества метода:
метод хорошо и быстро усваивается учащимися;
метод прост, удобен (не
учителю легко проверить соответствие построенного графика заданному уравнению;
метод может быть распространен и на другие, не только периодические функции, но именно для периодических функций его применение наиболее целесообразно.
Слайд 9Метод инверсии
Переход к применению инверсии
затруднителен, ибо в отличие
от движений плоскости
растяжений они неизвестны
школьникам и не так уж
наглядны, поэтому необходимо
мотивировать их введение.
Инверсия в филологии “близкие”,
“далёкие” точки от прямой.
Рисунок 3
Слайд 10Метод инверсии
Новая тема начинается с
рассмотрения графика
функции, изобразив который
необходимо обсудить:
будет ли пересекаться
как поведет себя искомый график там, где абсциссы его точек “близки” к единице;
как поведет себя график там, где абсциссы его точек “велики”.
Рисунок 3
Слайд 11Метод инверсии
Так как учащиеся знают, что если функция
y = f (
возрастает и принимает только положительные
значения, то
y = 1 / f (x ) убывает
Построение этого графика проходит достаточно
легко (они могут построить его самостоятельно).
Слайд 12
Метод инверсии
Определение инверсии относительно прямой:
! Точка В называется инвертной
эти точки лежат по одну сторону относительно оси L;
отрезок, их соединяющий, перпендикулярен оси L;
произведение расстояний от этих точек до L равно 1;
у точек оси инвертных точек нет.
Слайд 13Инверсия относительно оси ОХ
График:
q ( x ) = 1 /
получается из графика:
y = f ( x ),
инверсией относительно
оси ОХ.
Рисунок 4
Слайд 14Инверсия относительно оси ОУ
График:
q (x ) = f ( 1
получается из графика:
y = f ( x ),
инверсией относительно
оси ОУ.
Рисунок 5
Слайд 16Свойства инверсий и построение графиков
с их помощью:
доказываются теоремы;
разбираются образцы заданий;
пишутся самостоятельные
Например, для самостоятельной и домашней работы
предлагаются задания построить графики функций:
а) г)
б) д)
в) е)
Слайд 18Практическое применение инверсии
Рассмотренная тема находит свое применение в
уравнений и неравенств с параметрами графическим методом.
Он состоит в построении кривой, определяемой уравнением с
параметром:
После преобразования получаем:
(а - 1)х² - 4(а - 1)х + 3а – 4 = 0
Слайд 19Практическое применение инверсии
С помощью графика установить:
а) при каких значениях
б) при каких значениях параметра а уравнение имеет решения разных знаков;
в) при каких значениях параметра а уравнение имеет корень из отрезка [-1;2];
г) при каких значениях параметра а уравнение имеет корень больше 6.
Слайд 20Практическое применение инверсии
Рисунок 8
с помощью графика легко ответить на
графический способ дает единообразие рассуждений;
если решение вызывает сомнение, необходимо подкрепить выводы аналитически.
Слайд 21 По данной теме проводятся:
уроки-практикумы
коллоквиумы
презентации
Учащиеся к урокам
графики которых можно построить используя рассмотренные
преобразования.
График в силу своей наглядности является незаменимым в
исследовании поведения функции и в решении некоторых
уравнений и неравенств, в том числе и с параметром.
Практическое применение инверсии
Слайд 22Список используемой литературы
И.М. Гельфанд, Е.Г. Глаголева, Э.Э. Шноль Функции и графики
А.П. Карп Даю уроки математики…: Кн. для учителя: Из опыта работы. - М.: Просвещение, 1992.-191 с.