Н.П.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Математика и медицина автор Тихая Елена гр. 31Б
Содержание
- 1. Презентация Математика и медицина автор Тихая Елена гр. 31Б
- 2. Математическое моделирование как нормальных физиологических, так и
- 3. Разумеется, при исследовании биомедицинских проблем встречаются процессы,
- 4. Рассматривались биохимическая и электрокардиографическая модели инфаркта миокарда,
- 5. Слайд 5
- 6. Механическая (в рамках МСС) модель сердца рассматривалась
- 7. Слайд 7
- 8. По-видимому, на сегодняшней день наиболее адекватными представляются
- 9. Слайд 9
- 10. Рассматривался нестационарный квазипериодический режим кровообращения головного мозга.
- 11. Слайд 11
- 12. Слайд 12
- 13. Разработанные авторами вычислительные методы и алгоритмы позволяют
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Авторы работы не только строят такие модели,
- 18. Слайд 18
- 19. Другой пример — моделирование офтальмологической операции экстракции
- 20. Слайд 20
- 21. ЗАКЛЮЧЕНИЕГоворить о тесной связи математики и медицины
- 22. СПАСИБО ЗА ВНИМАНИЕ
Математическое моделирование как нормальных физиологических, так и патологических процессов является в настоящее время одним из самых актуальных направлений в научных исследованиях. Дело в том, что современная медицина Представляет собой в основном экспериментальную науку с огромным эмпирическим
Слайд 1МАТЕМАТИКА И МЕДИЦИНА
ВЫПОЛНИЛА СТУДЕНТКА ГБПОУ «НГК» Тихая Елена группа 31Б
РУКОВОДИТЕЛЬ БОБРОВА
Слайд 2Математическое моделирование как нормальных физиологических, так и патологических процессов
является в
настоящее время одним из самых
актуальных направлений в научных исследованиях.
Дело в том, что современная медицина
Представляет собой в основном экспериментальную
науку с огромным эмпирическим опытом воздействия
на ход тех или иных болезней различными
средствами. Что же касается подробного
изучения процессов в биосредах, то их экспериментальное исследование является ограниченным, и наиболее эффективным аппаратом их исследования представляется математическое моделирование. Разработка этого аппарата предполагает — построение замкнутой механико-математической модели процесса, описывающей поведение биологической среды на основе системы уравнений в частных производных механики сплошных сред (МСС);
актуальных направлений в научных исследованиях.
Дело в том, что современная медицина
Представляет собой в основном экспериментальную
науку с огромным эмпирическим опытом воздействия
на ход тех или иных болезней различными
средствами. Что же касается подробного
изучения процессов в биосредах, то их экспериментальное исследование является ограниченным, и наиболее эффективным аппаратом их исследования представляется математическое моделирование. Разработка этого аппарата предполагает — построение замкнутой механико-математической модели процесса, описывающей поведение биологической среды на основе системы уравнений в частных производных механики сплошных сред (МСС);
Слайд 3Разумеется, при исследовании биомедицинских проблем встречаются процессы, для математического описания которых
используются аппараты обыкновенных дифференцированных уравнений (ОДУ), систем алгебраических нелинейных уравнений. Примеры успешного использования таких математических аппаратов представлены в для прогнозирования развития болезни, для решения задач нелинейной динамики в биологии и др. Кроме того, при изучении некоторых медицинских процессов необходимо численно решать жёсткие системы ОДУ, например, при моделировании протекания химических реакций, что представляет собой самостоятельную проблему, которой посвящена обширная литература. Известно, что некоторые математические методы развивались под влиянием биомедицинских проблем, например, методы математической статистики, уравнение Вольтерра, нелинейные разностные отображения, теория хаоса и порядка, конечные автоматы, нейросети, методы решения жёстких ОДУ. Постановки биологических и медицинских задач, которые приводят к необходимости численного решения систем уравнений в частных производных (МСС, уравнения параболического и эллиптического типа), появились относительно недавно.
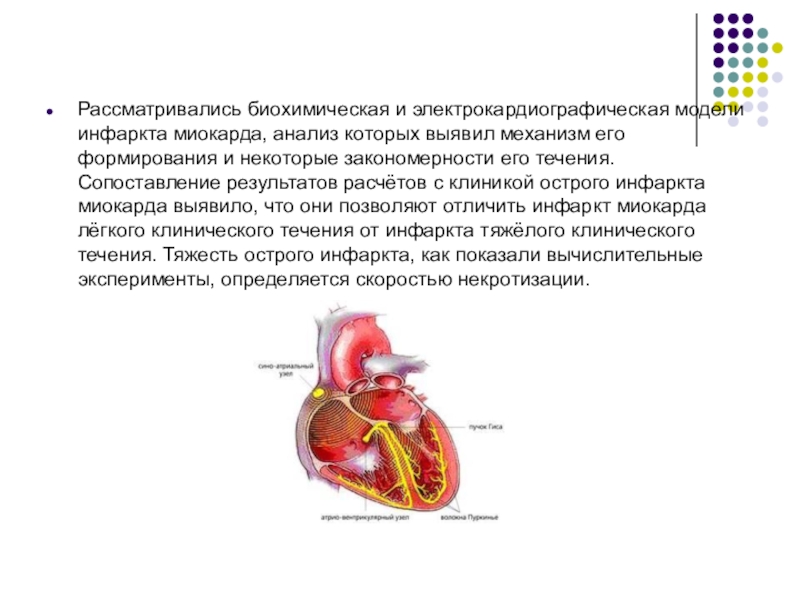
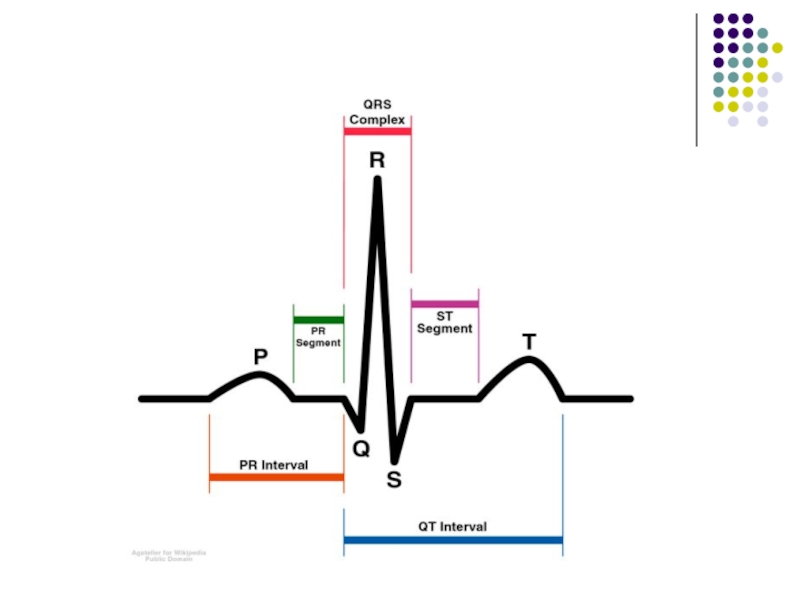
Слайд 4Рассматривались биохимическая и электрокардиографическая модели инфаркта миокарда, анализ которых выявил механизм
его формирования и некоторые закономерности его течения. Сопоставление результатов расчётов с клиникой острого инфаркта миокарда выявило, что они позволяют отличить инфаркт миокарда лёгкого клинического течения от инфаркта тяжёлого клинического течения. Тяжесть острого инфаркта, как показали вычислительные эксперименты, определяется скоростью некротизации.
Слайд 6Механическая (в рамках МСС) модель сердца рассматривалась в различных работах. Подобное
рассмотрение представляет большой интерес для клинической практики, так как изучение работы сердечной мышцы в условиях частичного изменения её механических характеристик позволит понять, как изменится функционирование всего сердца и кровеносной системы в условиях частичного некроза. Однако разработка полной физикоматематической трёхмерной модели, учитывающей электрохимические эффекты, их связь с напряжениями в сердечной мышце и численное решение соответствующей динамической пространственной задачи в рамках МСС, по-видимому, является перспективной проблемой. Исследование распространения импульсов Пуркинье (структуры кабельного типа, проводящие импульсы от пред- сердий до желудочков в сердце) проводится в работах . Основываясь на численном эксперименте с использованием математической модели Мак’Аллистера–Нобла–Тасена, описывающей динамику распространения импульсов в волокнах Пуркинье, авторы этих работ обнаружили различные режимы распространения таких импульсов. В частности, оказалось, что при различных режимах возбуждения возможно появление таких явлений, как отражения, автоколебания, аннигиляция, солитоноподобные режимы. Интересно, что подобные явления имеют место в нервных волокнах, возбуждение импульсов в которых описывается в рамках известной математической модели Ходжкина–Хаксли. Описание простейших математических моделей работы систем кровообращения и сердца можно найти в различной литературе.
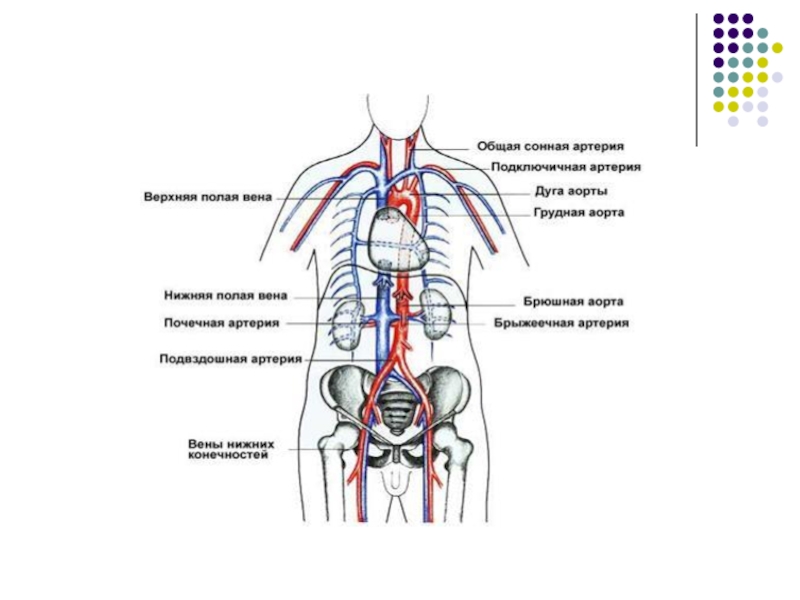
Слайд 8По-видимому, на сегодняшней день наиболее адекватными представляются динамические модели пульсирующих
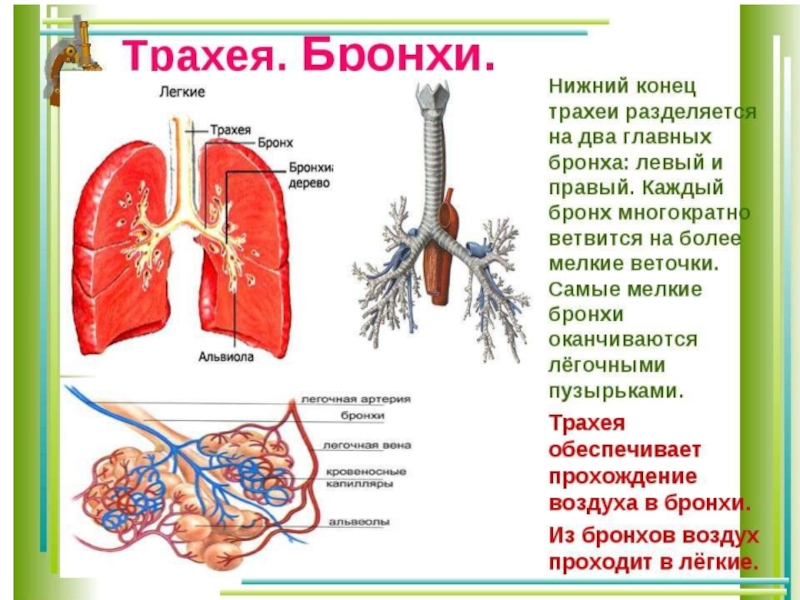
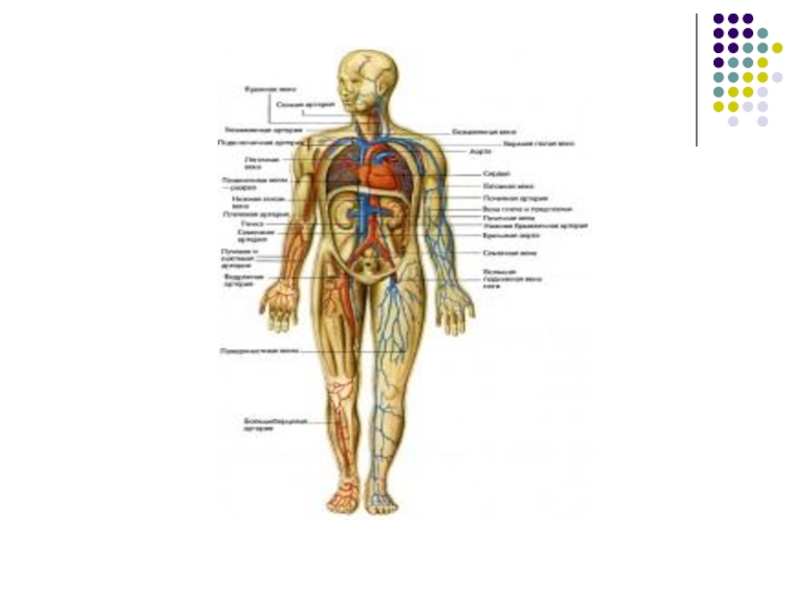
течений несжимаемой жидкости в системе растяжимых трубок. В работах использовалась квазиодномерная гидравлическая модель несжимаемой жидкости в деформируемом кровеносном сосуде переменного сечения, обобщённая на случай иерархической ветвящейся системы кровеносных сосудов факториальной структуры. Подобная же сетевая квазиодномерная модель использовалась и для математического описания работы дыхательной системы на участке трахея — бронхи. Иной подход моделирования был предложен функционирования кровеносной системы, базирующейся на квазитрёхмерной системе кровообращения. В этом случае моделированию подлежит изменение всех параметров, которые могут быть на выходе, например, концентрации активных веществ и давление в крови на разных участках кровеносной системы, а так- же скорости кровотока.
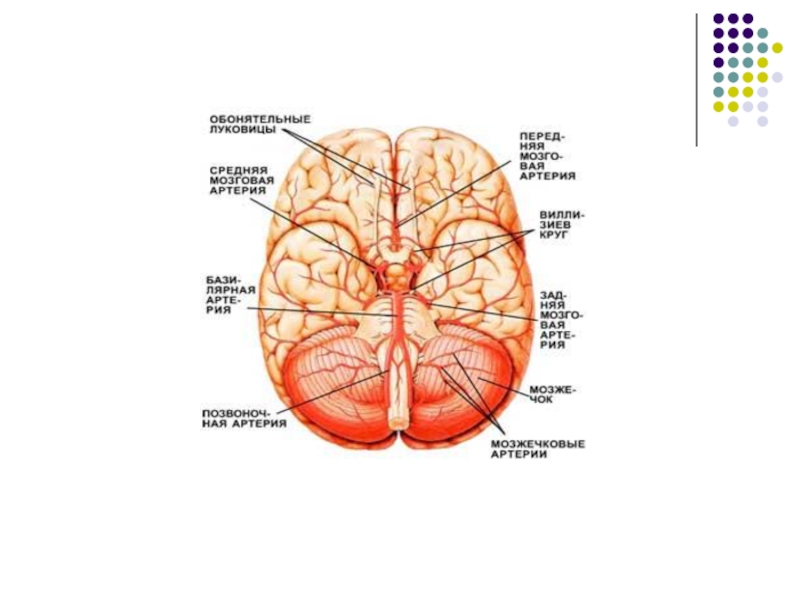
Слайд 10Рассматривался нестационарный квазипериодический режим кровообращения головного мозга. С учётом взаимодействия с
большим кругом кровообращения в другой работе рассчитана динамика изменения параметров крови в различных отделах головного мозга, подтверждена гипотеза о связи изменений объёма крови в процессе сердечного цикла с движением спинномозговой жидкости, возрастания амплитуды пульсовой волны, распространяющейся в сосудах Виллизиева круга и масштабных артерий в грудной и брюшной полости. По инициативе нейрохирургов Главного военного клинического госпиталя им. Н.Н. Бурденко и Института скорой помощи им. Н.В. Склифосовского была поставлена задача о расчёте последствий черепно-мозговых травм. Изучение областей повреждения мозга при различных динамических воздействиях на него путём математического моделирования в рамках МСС может дать важную информацию о последствиях травм. В нейрохирургической практике хорошо известен следующий факт: области поражения мозга при черепно-мозговых травмах не всегда совпадают с областями, прилежащими к месту удара. Примером этому является феномен «противоудара»: при ударе затылком область повреждения мозга локализуется в лобной части головного мозга. Объяснение этому явлению можно дать только путём проведения численного исследования сложнейших волновых процессов, образующихся в неоднородной механической конструкции, которая представляет собой систему череп–мозг. Кроме того, механико-математические модели реакции рассматриваемой механической системы на динамические нагрузки можно использовать как инструмент для изучения различных параметров травмы.
Слайд 13Разработанные авторами вычислительные методы и алгоритмы позволяют изучать также динамические процессы,
происходящие в теле человека, при воздействии динамических нагрузок. Такая задача оказывается весьма актуальной, поскольку появляется возможность предсказания областей и степеней поражения тела при каких-либо опасных нагрузках. Области приложения подобных задач очевидны (кроме медицинской): спортивные травмы, травмы при производстве опасных видов работ в экстремальных условиях (например, горные или взрывные работы), боевых и полицейских операциях, автомобильных, авиационных, иных техногенных катастрофах. К проблеме математического моделирования травматологических процессов относится и задача о залечивании ран. Численному изучению этого процесса посвящены работы , в которых получено количественное описание динамики залечивания резаной раны кожного покрова человека. Важнейшей областью в травматологии является проблема математического моделирования движения ног человека при ходьбе с целью построения ортопедических протезов, имитирующих их движение.
Слайд 17Авторы работы не только строят такие модели, но и реализуют их.
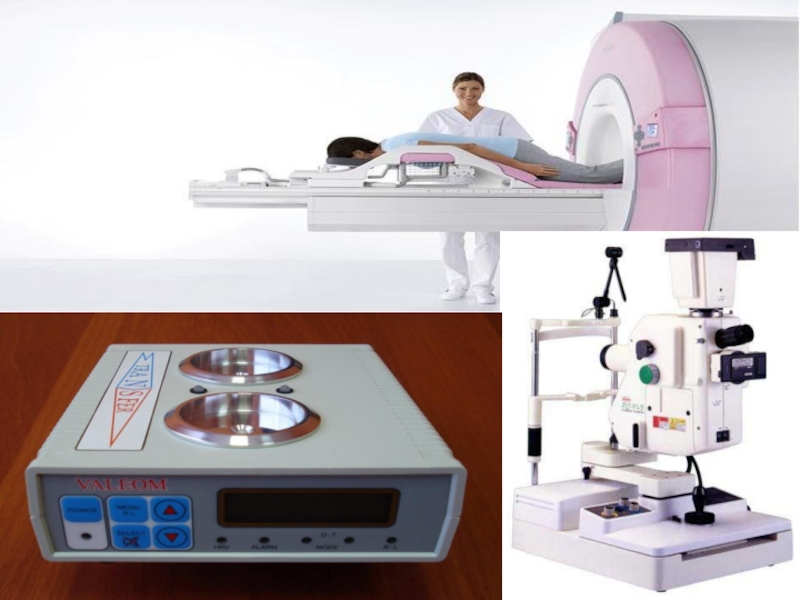
Для этих целей они использовали аппарат ОДУ. Однако для моделирования распределения динамических нагрузок и деформаций при перемещении полной стопы уже требуется использование аппарата дифференциальных уравнений в частных производных, в частности, системы уравнений МДТТ. Создание подобных моделей для нужд травматологии и ортопедии представляется но- вой и актуальной задачей вычислительной медицины. Перспективным направлением вычислительной медицины представляется компьютерная реализация виртуальных хирургических операций и предсказания их последствий. Разумеется, это очень сложное направление, которое только начинает появляться, а постановка некоторых задач до конца не ясна (например, моделирование работы хирурга с помощью скальпеля). Однако реализация некоторых виртуальных операций является реальной задачей. Так, в работе представлено численное моделирование операций литотрипсии (дробление почечных камней акустическим волнами, инициируемыми искровым разрядом или лазерным импульсом). Цель таких исследований — найти режимы работы литотриптора (длительность и интенсивность импульса, количество им- пульсов), при которых фрагменты разрушенного камня были бы достаточно малыми для их выведения из организма естественным путём. Для этого численно исследовалась картина распространения акустического импульса в теле и в камне, а также решалась задача его разрушения.
Слайд 19
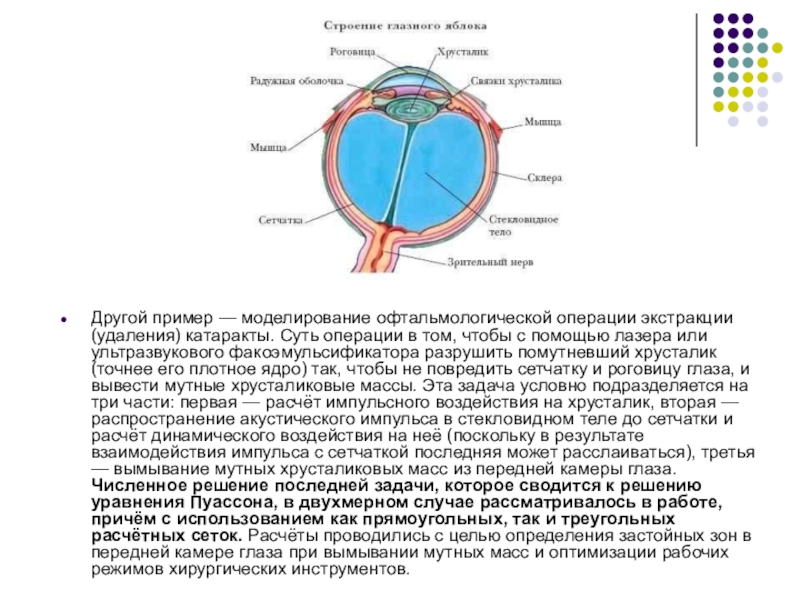
Другой пример — моделирование офтальмологической операции экстракции (удаления) катаракты. Суть операции
в том, чтобы с помощью лазера или ультразвукового факоэмульсификатора разрушить помутневший хрусталик (точнее его плотное ядро) так, чтобы не повредить сетчатку и роговицу глаза, и вывести мутные хрусталиковые массы. Эта задача условно подразделяется на три части: первая — расчёт импульсного воздействия на хрусталик, вторая — распространение акустического импульса в стекловидном теле до сетчатки и расчёт динамического воздействия на неё (поскольку в результате взаимодействия импульса с сетчаткой последняя может расслаиваться), третья — вымывание мутных хрусталиковых масс из передней камеры глаза. Численное решение последней задачи, которое сводится к решению уравнения Пуассона, в двухмерном случае рассматривалось в работе, причём с использованием как прямоугольных, так и треугольных расчётных сеток. Расчёты проводились с целью определения застойных зон в передней камере глаза при вымывании мутных масс и оптимизации рабочих режимов хирургических инструментов.
Слайд 21ЗАКЛЮЧЕНИЕ
Говорить о тесной связи математики и медицины можно бесконечно. Наука движется
вперед, открывая все новые возможности. Некоторые из них на грани фантастики. Это неоспоримый факт.
Я много узнала, готовя этот материал, узнайте же и Вы.
Спасибо.
Я много узнала, готовя этот материал, узнайте же и Вы.
Спасибо.