- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к выступлению на сетевой конференции
Содержание
- 1. Презентация к выступлению на сетевой конференции
- 2. Сетевая научно – практическая конференция по математике, физике и информатике «Путь к успеху».
- 3. Цель Выяснить, как с помощью «кругов
- 4. ПроблемаНе знаем, как решить логическую задачу.АктуальностьРешение логических
- 5. Объекты исследованияМножество.Пересечение множеств.Объединение множеств.Предмет исследования«Круги Эйлера».Метод исследованияСравнительный анализ.
- 6. При решении целого ряда задач Леонард Эйлер
- 7. Диаграммы Эйлера (круги Эйлера) — геометрическая схема, с помощью
- 8. (1707 – 1783)«Учиться всему надо легко, доступно и наглядно».Леонард Эйлер
- 9. Леонардо Эйлер (1707 – 1783)Знаменитый математик, механик,
- 10. Множество – это совокупность элементов, обладающих некоторым общим свойством.
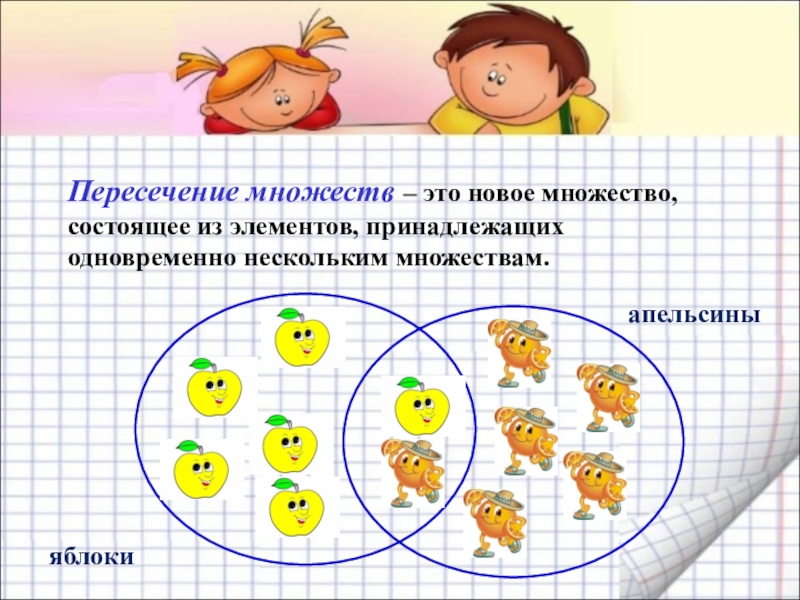
- 11. Пересечение множеств – это новое множество, состоящее из элементов, принадлежащих одновременно нескольким множествам.яблокиапельсины
- 12. Объединение множеств– это новое множество, состоящее из элементов, принадлежащих хотя бы одному из множеств
- 13. Запишем на символическом языке соотношения между множествами.А
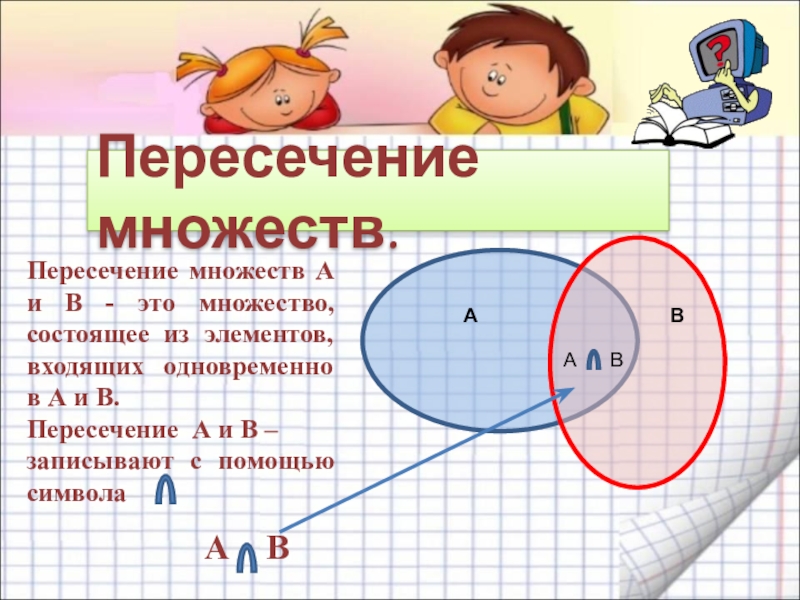
- 14. Пересечение множеств.Пересечение множеств А и В
- 15. Пересечение множеств.Пусть А = { 2,
- 16. Объединение множеств.Объединением множеств А и B
- 17. Объединение множеств.Пусть А = { 2,
- 18. Круги Эйлера — геометрическая схема, с помощью которой можно
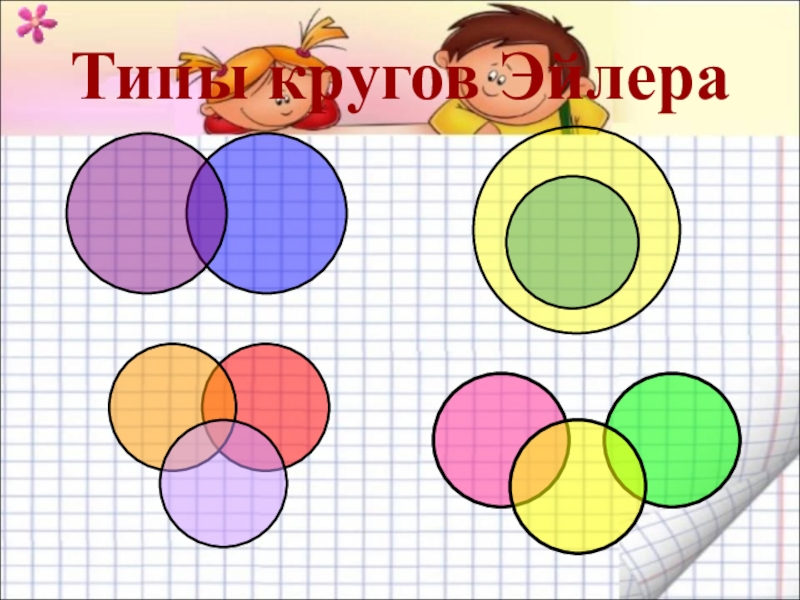
- 19. Типы кругов Эйлера
- 20. Алгоритм решения логических задач определённого вида с
- 21. 25ПР-1434631Результаты опроса жильцов дома о том, смотрели
- 22. 25ПР-14346311.Сколько человек не смотрело ни тот, ни
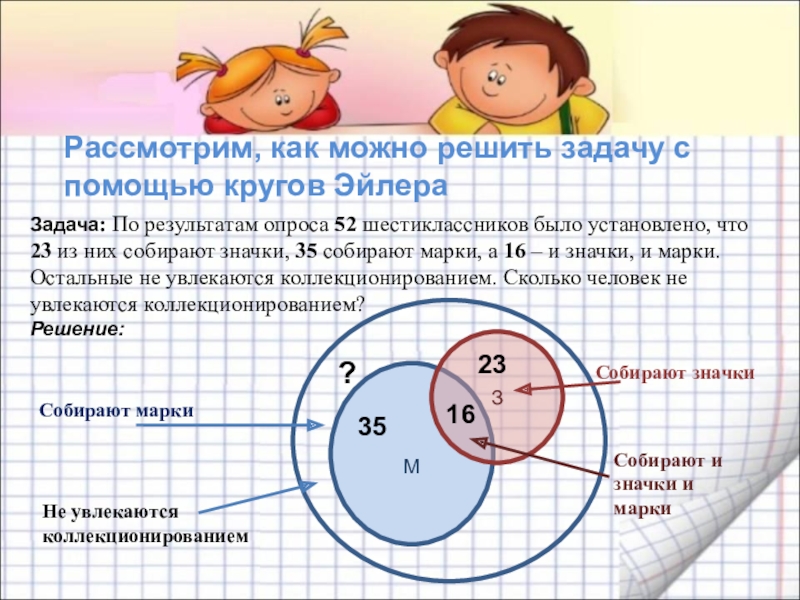
- 23. Рассмотрим, как можно решить задачу с помощью
- 24. Решение задачи 1) Значки и марки собирают
- 25. Решить задачуВ математической олимпиаде для 6-кл. участвовали
- 26. Задание . На полке стояло 25
- 27. 1. Обозначим: P- множество книг, прочитанных
- 28. На кружке по математике была представлена данная
- 29. Слайд 29
- 30. ЗаключениеВ процессе нашей работы, мы научились грамотно
- 31. 4. Теоретическая значимость заключается в разработке способа
Слайд 2
Сетевая
научно – практическая конференция по математике, физике и информатике
«Путь
Слайд 3
Цель
Выяснить, как с помощью «кругов Эйлера» можно решать
Задачи
Изучить теоретический материал: биографию Леонарда Эйлера, «круги Эйлера».
Научиться применять круги в решении логических задач.
Провести исследование по классификации задач.
Сформулировать алгоритм решения задач.
Слайд 4
Проблема
Не знаем, как решить логическую задачу.
Актуальность
Решение логических задач способствует повышению интеллектуального
Гипотеза
Существует способ решения задачи с громоздким условием и со многими данными. Этот способ должен быть простым и не требовать особых умозаключений.
Слайд 5
Объекты исследования
Множество.
Пересечение множеств.
Объединение множеств.
Предмет исследования
«Круги Эйлера».
Метод исследования
Сравнительный анализ.
Слайд 6
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств
Слайд 7
Диаграммы Эйлера (круги Эйлера) — геометрическая схема, с помощью которой можно изобразить отношения
Слайд 9Леонардо Эйлер (1707 – 1783)
Знаменитый математик, механик, физик и астроном, Л.Эйлер
Рассмотрим, действительно ли это так ?
Слайд 11
Пересечение множеств – это новое множество, состоящее из элементов, принадлежащих одновременно
яблоки
апельсины
Слайд 12
Объединение множеств– это новое множество, состоящее из элементов, принадлежащих хотя бы
Слайд 13Запишем на символическом языке соотношения между множествами.
А и В
А и С
С
А, В и С
С
В
А
А B
A C
B C
A B C
A является подмножеством множества В, а В является подмножеством множества С
Слайд 14Пересечение множеств.
Пересечение множеств А и В - это множество, состоящее
Пересечение А и В –
записывают с помощью символа
А В
В
А
А В
Слайд 15Пересечение множеств.
Пусть А = { 2, 4, 6} , a
Пересечение множеств А и В
А В = А
В
А
Слайд 16Объединение множеств.
Объединением множеств А и B называют множество, состоящее из
Объединение множеств А и В обозначают символом
В
А
Слайд 17Объединение множеств.
Пусть А = { 2, 4, 6} , a
Объединение множеств А и В
А В = В
В
А
Слайд 18
Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами,
Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче.
Слайд 20
Алгоритм решения логических задач определённого вида
с помощью кругов Эйлера
Записать краткое
Выполнить рисунок.
Записать данные в круги.
Анализировать, рассуждать и записывать результаты в части кругов.
Записать решение и ответ.
Слайд 21
25
П
Р-1
43
46
31
Результаты опроса жильцов дома о том, смотрели ли они в новогоднюю
Используя данные на схеме, можно ответить вопросы:
Слайд 22
25
П
Р-1
43
46
31
1.Сколько человек не смотрело ни тот, ни другой канал?
2. Сколько человек
3. Сколько человек смотрело только Первый канал?
4. Сколько человек смотрело канал Россия-1?
5. Сколько человек смотрело хотя бы один из этих каналов?
(25)
(46)
(31+46)
(43)
(120)
Слайд 23Рассмотрим, как можно решить задачу с помощью кругов Эйлера
Задача: По результатам
Решение:
М
З
Собирают значки
Не увлекаются
коллекционированием
Собирают марки
Собирают и значки и марки
?
23
35
16
Слайд 24Решение задачи
1) Значки и марки собирают 16 человек. Впишем число
2) Значки собирают 23 человека. Тогда только значки собирают: 23-16 = 7 человек. Впишем число 7 в свободную часть круга З
3) Только марки собирают: 35-16 = 19 человек. Занесем число 19 в схему.
4) Теперь мы можем узнать, сколько человек занимаются коллекционированием: 16+7+19 = _______ человека
5) Не занимаются коллекционированием:
52 - __ = __________ человек.
Ответ: _____ человек.
М
З
19
16
7
10
Слайд 25
Решить задачу
В математической олимпиаде для 6-кл. участвовали 50 человек. Из
Покажите на схеме решение задачи.
А
Г
30
10
10
40 человек
20 человек
Слайд 26 Задание . На полке стояло 25 волшебных книг по заклинаниям,
При этом не было не одной книги, которую бы прочитали все.
4 книги прочитали и Гарри Поттер, и Рон.
Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер.
Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитали только Гарри Поттер и только Рон?
Слайд 271. Обозначим: P- множество книг,
прочитанных Гарри Поттером;
R-множество книг,
прочитанных
G- множество книг, прочитанных Гермионой
2. Расставим известные данные в круги Эйлера.
3.Найдем количество книг, которые прочитал только Гарри Поттер: 11 - 4 - 2 = 5 книг.
4. А теперь, чтобы узнать количество прочитанных книг только
Роном, нужно из всего количества книг вычесть известное количество прочитанных книг: 25 ― (11+7)= 7 книг прочел только Рон.
R
P
G
7
2
4
5
7
Слайд 28
На кружке по математике была представлена данная работа. И учащимся
6-го
Слайд 30Заключение
В процессе нашей работы, мы научились грамотно оперировать такими понятиями, как
Наша гипотеза подтвердилась. Применение кругов Эйлера позволяет без затруднений и с маленькими затратами времени решать логические задачи с громоздким условием и со многими данными.
Практическая значимость нашей работы заключается в расширении возможностей решения логических задач.
Слайд 31
4. Теоретическая значимость заключается в разработке способа действий при решении логических
5. Задачи, решаемые с помощью кругов Эйлера предлагаются на олимпиадах по математике и информатике. Теперь мы сможем узнавать такие задачи и быстро их решать.
6. Нашу работу мы использовали на внеурочных занятиях по математике для 6 классов.