- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к внеклассному мероприятию Урок суд над геометрией Лобачевского
Содержание
- 1. Презентация к внеклассному мероприятию Урок суд над геометрией Лобачевского
- 2. Открытие Н. И. Лобачевским
- 3. Евклид (III век до н. э.) Древнегреческий
- 4. Был мудрым Евклид, Но его параллели,Как будто
- 5. Н. И. Лобачевский
- 6. Основные понятия геометрии Лобачевского.АбсолютаНа евклидовой плоскости E
- 7. Через любые две точки можно провести прямую.Прямая
- 8. На плоскости через точку не лежащую на
- 9. 1.Пусть прямые а' и а" не пересекаются
- 10. Далее Н.И.Лобачевский утверждал, что две параллельные прямые
- 11. В геометрии Евклида:Сумма углов любого треугольника равна 180 градусам.Сумма углов треугольника
- 12. В геометрии Лобачевского: Возьмём треугольник с
- 13. Основными объектами на плоскости Лобачевского являются пучки
- 14. Неевклидовыми углами являются угол между пересекающимися окружностями,
- 15. Д е н ь р о
- 16. Все! Перечеркнуты “Начала”. Довольно мысль на них
- 17. Модель Клейна
- 18. Бутылка КлейнаВ 1882г немецкий математик Феликс Христиан
- 19. Применение геометрии Лобачевского в реальном миреГеометрия Евклида
- 20. Модель БельтрамипсевдосфераЭудженио Бельтрами (1835-1900) нашел модель для
- 21. Решение суда Несмотря на все кажущиеся
- 22. Слайд 22
Слайд 2 Открытие Н. И. Лобачевским геометрии, отличной от евклидовой,
описывающей свойства
окружающего нас
пространства.
Слайд 3Евклид (III век до н. э.)
Древнегреческий математик, автор первого трактата
по
Евклид (иначе Эвклид) – древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Биографические сведения об Евклиде крайне скудны. Известно лишь, что учителями Евклида в Афинах были ученики Платона,он преподавал в Александрийской академии. Евклид – первый математик александрийской школы.
Главная работа Евклида– "Начала"– содержит изложение планиметрии, На протяжении более двух тысячелетий евклидовы "Начала" оставались основным трудом по элементарной математике.
Слайд 4Был мудрым Евклид,
Но его параллели,
Как будто бы вечные сваи легли.
И мысли его, что как стрелы летели,
Всегда оставались в пределах Земли.
А там, во вселенной, другие законы,
Там точками служат иные тела.
И там параллельных лучей миллионы
Природа сквозь Марс, может быть, провела.
Слайд 5
Н. И. Лобачевский родился в Нижнем Новгороде.
и только что основанный
Казанский Императорский
университет, которому
отдал 40 лет жизни.
Казанский императорский университет, 1840-е гг.
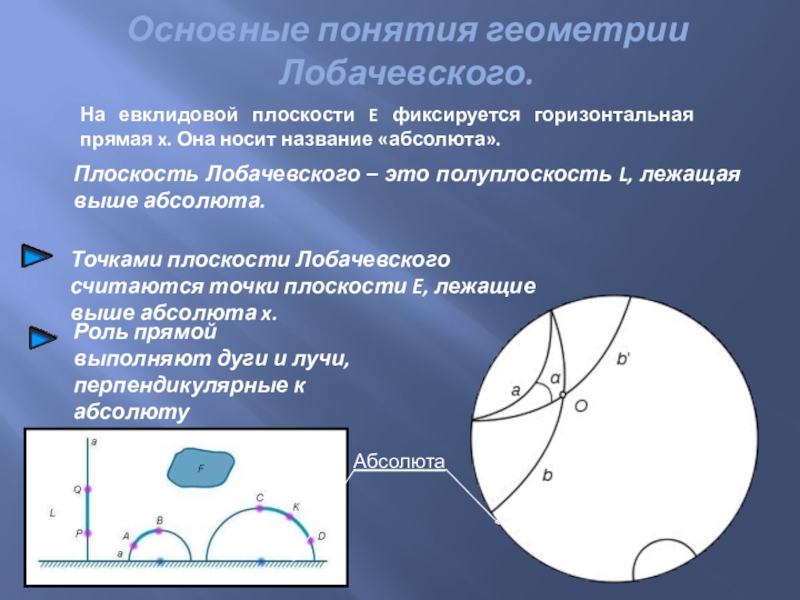
Слайд 6Основные понятия геометрии Лобачевского.
Абсолюта
На евклидовой плоскости E фиксируется горизонтальная прямая x.
Плоскость Лобачевского – это полуплоскость L, лежащая выше абсолюта.
Слайд 7Через любые две точки можно провести прямую.
Прямая продолжается бесконечно.
Из любого центра
Все прямые углы равны между собой.
1. От всякой точки до всякой точки можно провести прямую.
2.Ограниченную прямую можно непрерывно продолжать по прямой.
3. Из всякого центра всяким раствором может быть описан круг.
4. Все прямые углы равны между
собой
Слайд 8На плоскости через точку не лежащую на данной прямой, проходит прямая
На плоскости через точку, не лежащую на данной прямой, проходит более чем одна прямая, не пересекающая данную.
7
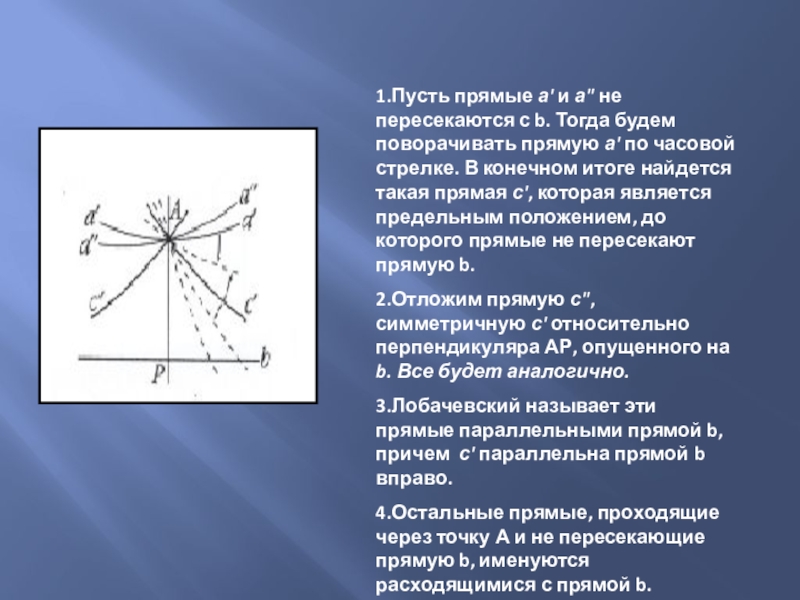
Слайд 91.Пусть прямые а' и а" не пересекаются с b. Тогда будем
2.Отложим прямую с", симметричную с' относительно перпендикуляра АР, опущенного на b. Все будет аналогично.
3.Лобачевский называет эти прямые параллельными прямой b, причем с' параллельна прямой b вправо.
4.Остальные прямые, проходящие через точку А и не пересекающие прямую b, именуются расходящимися с прямой b.
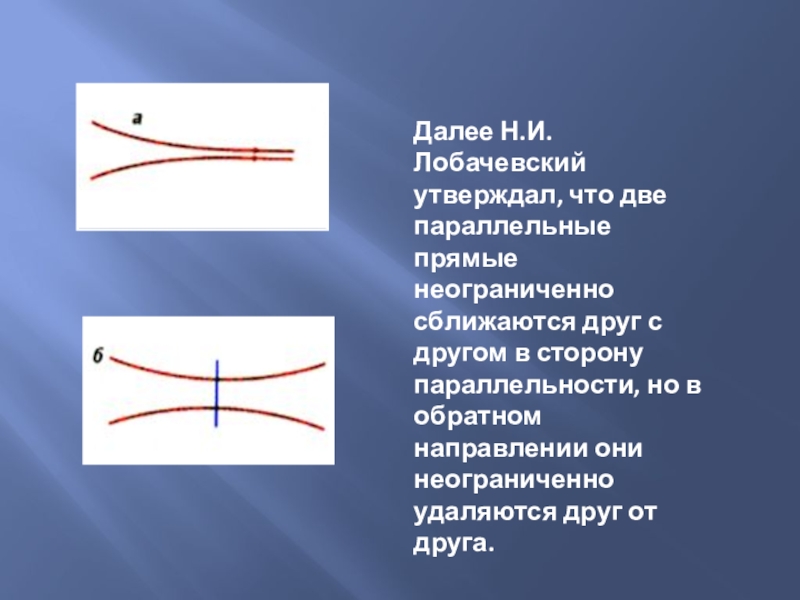
Слайд 10Далее Н.И.Лобачевский утверждал, что две параллельные прямые неограниченно сближаются друг с
Слайд 11
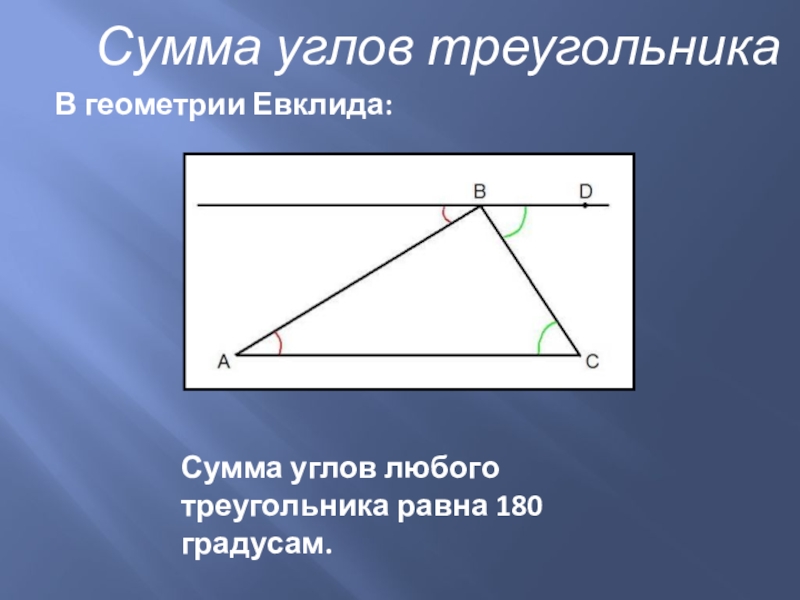
В геометрии Евклида:
Сумма углов любого треугольника равна 180 градусам.
Сумма углов треугольника
Слайд 12В геометрии Лобачевского:
Возьмём треугольник с точками NLK, где N
Так на шаре выглядит треугольник АВС образованный красной, синей и зелёной прямыми
K
N
L
Сумма углов треугольника
Слайд 13Основными объектами на плоскости Лобачевского являются пучки прямых.
На плоскости Лобачевского
Параллельные
Пересекающиеся
Расходящиеся
Геометрия Лобачевского
Слайд 14Неевклидовыми углами являются угол между пересекающимися окружностями, а также между окружностью
Таким образом величины неевклидовых углов определяются через величины соответствующих евклидовых углов.
Слайд 15Д е н ь р о ж д е н
23 (11) февраля 1826 года Н. И. Лобачевский впервые выступил с изложением своей геометрии перед учеными физико-математического факультета Казанского университета. Этот день считают днем рождения геометрии Лобачевского.
Титульный лист первого издания «Воображаемой геометрии»
Слайд 16
Все! Перечеркнуты “Начала”.
Довольно мысль на них скучала,
Хоть прав почти
Но быть не вечно постоянству:
И плоскость свернута в пространство,
И мир
Иной имеет вид...
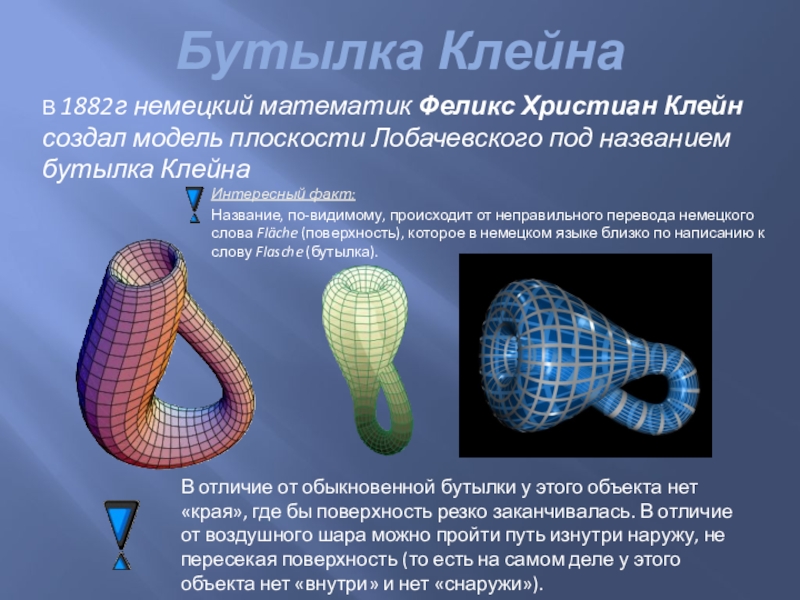
Слайд 18Бутылка Клейна
В 1882г немецкий математик Феликс Христиан Клейн создал модель плоскости
Название, по-видимому, происходит от неправильного перевода немецкого слова Fläche (поверхность), которое в немецком языке близко по написанию к слову Flasche (бутылка).
В отличие от обыкновенной бутылки у этого объекта нет «края», где бы поверхность резко заканчивалась. В отличие от воздушного шара можно пройти путь изнутри наружу, не пересекая поверхность (то есть на самом деле у этого объекта нет «внутри» и нет «снаружи»).
Интересный факт:
Слайд 19Применение геометрии Лобачевского в реальном мире
Геометрия Евклида является частным случаем геометрии
Как пример можно привести тот факт, что видимый звездный свод это ни что иное, как предельная плоскость. Астрономам после признания достижений Лобачевского пришлось пересчитывать все расстояния между звездами – и ошибки достигали 1/6.
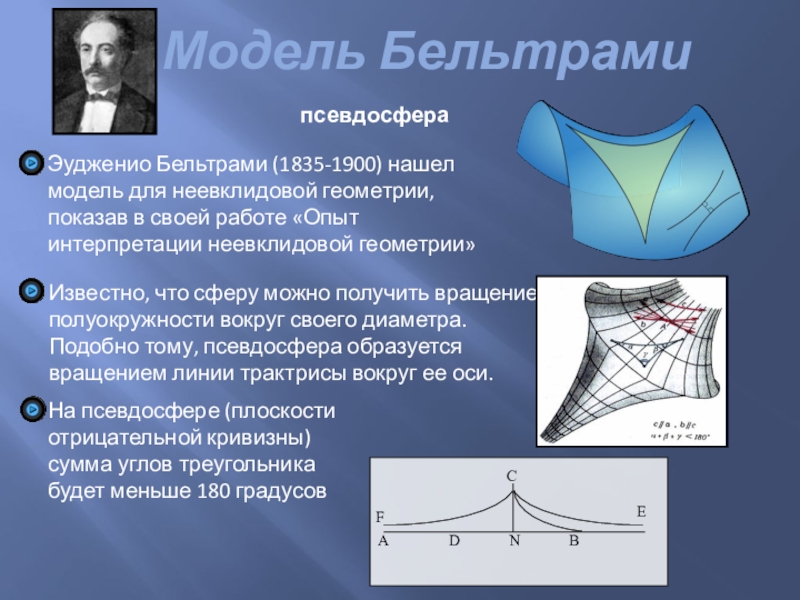
Слайд 20Модель Бельтрами
псевдосфера
Эудженио Бельтрами (1835-1900) нашел модель для неевклидовой геометрии, показав в
Известно, что сферу можно получить вращением полуокружности вокруг своего диаметра. Подобно тому, псевдосфера образуется вращением линии трактрисы вокруг ее оси.
На псевдосфере (плоскости отрицательной кривизны) сумма углов треугольника будет меньше 180 градусов