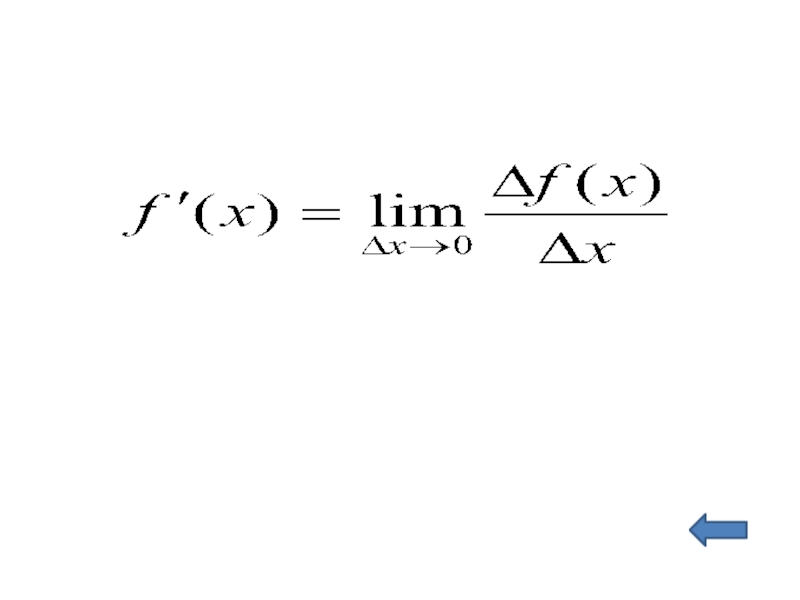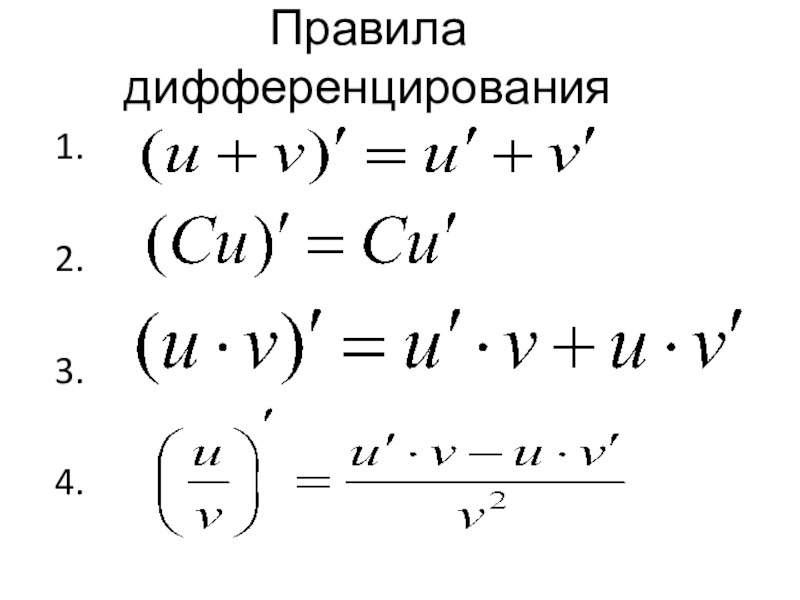или ином деле.»
Алексей Николаевич Крылов
(1863-1945)
Советский кораблестроитель, механик и математик, академик
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Применение производной для решения задач судовождения
Содержание
- 1. Презентация к уроку Применение производной для решения задач судовождения
- 2. Цель урока: формирование умений применять полученные
- 3. Производная.Дайте определение производной.В чем заключается физический смысл
- 4. Слайд 4
- 5. v(t)= x’(t) Производная от координаты точки по
- 6. Нахождение производной функции в точке– это вычисление
- 7. 1. Уравнение касательной к графику функции в
- 8. 1.Производная функции равна 0; 1; с.0
- 9. 2.Производная функции равна 0; 1; х.1
- 10. 3.Производная функции равна х; 2х; х2. 2х
- 11. 4.Производная функции
- 12. 5.Производная функции
- 13. 6.Производная функции
- 14. 7.Производная функции
- 15. 8.Производная функции
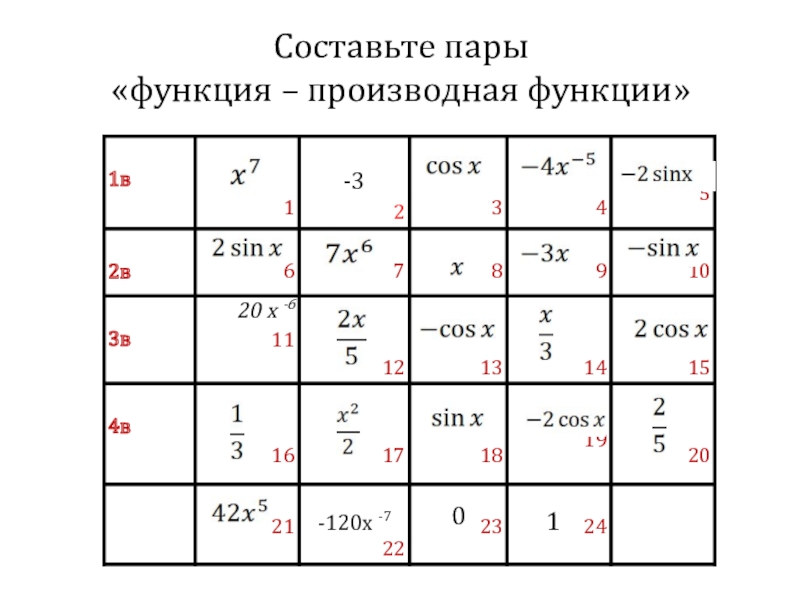
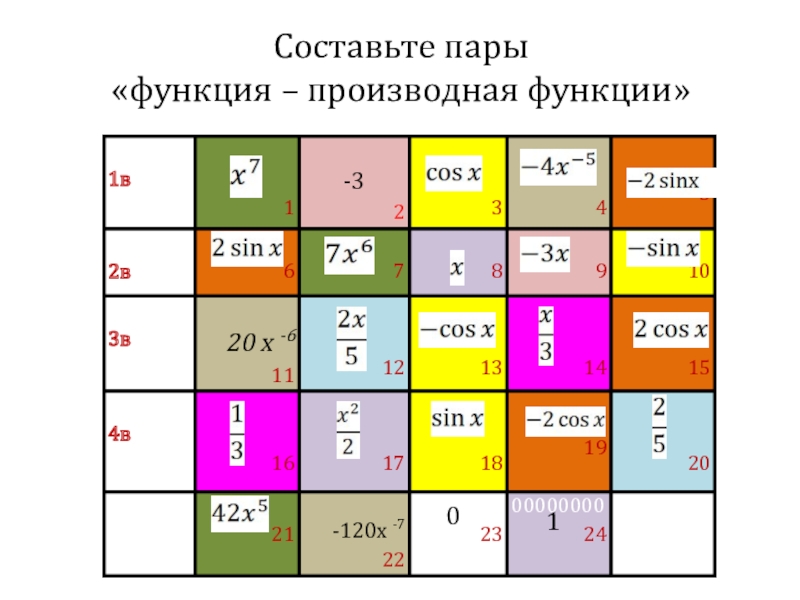
- 16. Составьте пары «функция – производная функции»01
- 17. Составьте пары «функция – производная функции»01
- 18. Проверка: 1 вариант: 1—7, 2—23, 3—10,
- 19. Правила дифференцирования1. 2.3.4.
- 20. Найти производную функции
- 21. Найти производную функции
- 22. Для каких целей, по вашему мнению, может
- 23. Какие задачи из других изучаемых дисциплин решались
- 24. Задача Судно движется прямолинейно по
- 25. Слайд 25
- 26. Какие задачи с практическим содержанием вы решали
- 27. ababНаибольшее , наименьшее значение функции на интервале.Если
- 28. Алгоритм нахождения наибольшего и наименьшего значения функции
- 29. Основные этапы, при решении задач прикладного характера
- 30. Экономический расчет рейса.Стоимость топлива необходимого для движения
- 31. 1. Формализация (перевод задачи на математический язык
- 32. f(v) = S/v = k·v2 + b/v
- 33. f(v) = k·v2 + b/v v –
- 34. 2. Решение математической задачи: ( алгоритм исследования
- 35. f'(v) = 136·v – 408000/v2Отметить критические точки
- 36. Определим дополнительную прибыль за рейс f(v) =
- 37. b = 408 000 руб. , k
- 38. Дополнительная прибыльS1 - S2 = 3 234
- 39. Домашнее задание 1.Теплоход движется по прямой согласно
- 40. Надо ли знать формулы для вычисления
Цель урока: формирование умений применять полученные знания при решении профессиональных задач судовождения, решаемых с использованием производной. Применение производной при решении задач судовождения.
Слайд 2Цель урока: формирование умений применять полученные знания при решении профессиональных
задач судовождения, решаемых с использованием производной.
Применение производной при решении задач судовождения.
Слайд 3Производная.
Дайте определение производной.
В чем заключается физический смысл производной.
Каков геометрический смысл производной?
Какие
задачи можно решить при помощи производной?
Что необходимо знать, чтобы решать задачи на нахождение производной элементарных функций?
Что необходимо знать, чтобы решать задачи на нахождение производной элементарных функций?
Слайд 5v(t)= x’(t)
Производная от координаты точки по времени есть скорость.
Производная
от скорости по времени есть ускорение
Кратко: производная функции – это скорость изменения этой функции
Кратко: производная функции – это скорость изменения этой функции
Слайд 6Нахождение производной функции
в точке– это вычисление углового
коэффициента касательной к
данной
функции в этой точке.
f’(x0 ) = tqα
функции в этой точке.
f’(x0 ) = tqα
Слайд 71. Уравнение касательной к графику функции в заданной точке. 2. Задачи на
нахождение скорости изменения функции.
3. Определение промежутков монотонности функции
4. Определение точек экстремума функции
5. Задачи на наибольшее и наименьшее значение (оптимизацию).
Слайд 18Проверка: 1 вариант: 1—7, 2—23, 3—10, 4—11, 5—19. 2 вариант: 6—15, 7—21, 8—24,
9—2, 10—13.
3 вариант: 11—22, 12—20, 13—18, 14—16, 15—5.
4 вариант: 16—23, 17—8, 18—3, 19—6, 20—23.
перевод в оценку:
«5» – 5 правильных ответов
«4» – 3-4 правильных ответа
«3» – 2 правильных ответа
Слайд 22Для каких целей, по вашему мнению, может применятся производная в судовождении?
Основная
задача судовождения – определение места судна в море.
Главные понятия:
Навигационный параметр(скорость, направление, углы, расстояния, разности расстояний и т.п.)
Навигационный ориентир(объекты с отличительными признаками и известным положением)
Навигационная функция – математическое выражение, устанавливающая связь между навигационным параметром и координатами места судна - U = f(x, y, t, φ, λ)
Главные понятия:
Навигационный параметр(скорость, направление, углы, расстояния, разности расстояний и т.п.)
Навигационный ориентир(объекты с отличительными признаками и известным положением)
Навигационная функция – математическое выражение, устанавливающая связь между навигационным параметром и координатами места судна - U = f(x, y, t, φ, λ)
Слайд 23Какие задачи из других изучаемых дисциплин решались на уроках математики с
использованием производной?
В чем заключается физический смысл производной?
Как определить скорость тела, пользуясь понятием производной, если задано уравнение движения тела?
Производная – это скорость.
Скорость судна – это навигационный параметр?
Если известно уравнение движения судна, как найти его скорость?
Слайд 24
Задача
Судно движется прямолинейно по закону
x - в милях, t
– часах.
а) Выведите формулу для вычисления скорости движения в любой момент времени t.
б) Найдите скорость судна в момент времени t = 2.1 часа.
в) Через сколько часов после начала движения теплоход остановится?
а) Выведите формулу для вычисления скорости движения в любой момент времени t.
б) Найдите скорость судна в момент времени t = 2.1 часа.
в) Через сколько часов после начала движения теплоход остановится?
Слайд 26Какие задачи с практическим содержанием вы решали на уроках математики?
Задачи
на наибольшее и наименьшее значение функции на отрезке.
Задачи на наибольшее и наименьшее. значение функции на интервале.
Задачи на оптимизацию.
Задачи на наибольшее и наименьшее. значение функции на интервале.
Задачи на оптимизацию.
Слайд 27a
b
a
b
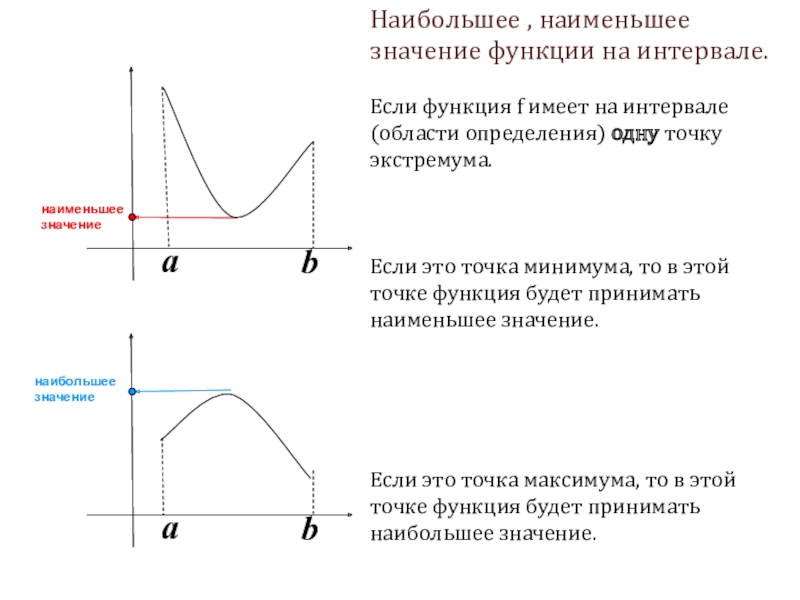
Наибольшее , наименьшее значение функции на интервале.
Если функция f имеет на
интервале (области определения) одну точку экстремума.
Если это точка минимума, то в этой точке функция будет принимать наименьшее значение.
Если это точка максимума, то в этой точке функция будет принимать наибольшее значение.
Если это точка минимума, то в этой точке функция будет принимать наименьшее значение.
Если это точка максимума, то в этой точке функция будет принимать наибольшее значение.
Слайд 28Алгоритм нахождения наибольшего и наименьшего значения функции на интервале.
Найти производную функции.
Найти
критические точки функции
Найти область определения функции (интервал исследования)
Найти область определения функции (интервал исследования)
Отметить интервал и критические точки на числовой прямой
Определить знаки производной на получившихся промежутках
Определить вид экстремума
Слайд 29Основные этапы, при решении задач прикладного характера на оптимизацию:
Формализация (перевод задачи
на математический язык – составление математической задачи);
решение полученной математической задачи;
интерпретация найденного решения.
решение полученной математической задачи;
интерпретация найденного решения.
Слайд 30Экономический расчет рейса.
Стоимость топлива необходимого для движения т/х «Амур» пропорциональна кубу
его скорости и составляет 68000 рублей при скорости 10 узлов. Все другие виды расходов составляют 408 000 рублей. Найдите наиболее экономическую скорость движения и вычислите дополнительную прибыль за экономию топлива на рейс Архангельск – Нарьян – Мар (расстояние 1250 км).
Слайд 311. Формализация (перевод задачи на математический язык – составление математической задачи);
Расходы
на эксплуатацию судна на 1 милю пути определяются по формуле
S = k·v3 + b, где
K – коэффициент пропорциональности
V – скорость судна в узлах
b – прочие виды расходов в рублях.
На практике расходы рассчитывают не на 1 милю пути, а на 1 час, поэтому функция определяющая расходы будет иметь вид
f(v) = S/v = (k·v3 + b)/v = k·v2 + b/v
S = k·v3 + b, где
K – коэффициент пропорциональности
V – скорость судна в узлах
b – прочие виды расходов в рублях.
На практике расходы рассчитывают не на 1 милю пути, а на 1 час, поэтому функция определяющая расходы будет иметь вид
f(v) = S/v = (k·v3 + b)/v = k·v2 + b/v
Слайд 32f(v) = S/v = k·v2 + b/v
Наиболее экономичная скорость –это какая
скорость?
При которой расходы будут минимальны.
Как сформулировать математическую задачу?
Исследовать функцию f(v) = S/v= k·v2 + b/v на минимум.
При которой расходы будут минимальны.
Как сформулировать математическую задачу?
Исследовать функцию f(v) = S/v= k·v2 + b/v на минимум.
Слайд 33f(v) = k·v2 + b/v
v – неизвестное.
Стоимость топлива
необходимого для движения т/х «Амур» пропорциональна кубу его скорости и составляет 68000 рублей при скорости 10 узлов. Все другие виды расходов составляют 408 000 рублей. Найдите наиболее экономическую скорость движения и вычислите дополнительную прибыль за экономию топлива на рейс Архангельск – Нарьян – Мар (расстояние 1250 км).
b = 408 000 руб.
Стоимость топлива
T = k·v3
68000 = k· 103
k = 68000/1000 =68
Получаем функцию
f(v) = 68·v2 + 408000/v
Исследовать данную функцию на минимум
Слайд 342. Решение математической задачи: ( алгоритм исследования функции на экстремум). f(v) = 68·v2
+ 408000/v
Найти производную функции.
Найти критические точки функции
Найти область определения функции?
f'(v) =(68·v2 + 408000/v)’=
= 68·2·v – 408000/v2
f'(v) = 68·2·v – 408000/v2 =0
(136·v3 – 408000)/v2 =0
v≠0, 136·v3 – 408000 = 0
v 3 = 408000 /136 = 3000
v ≈ 14.5
V > 0
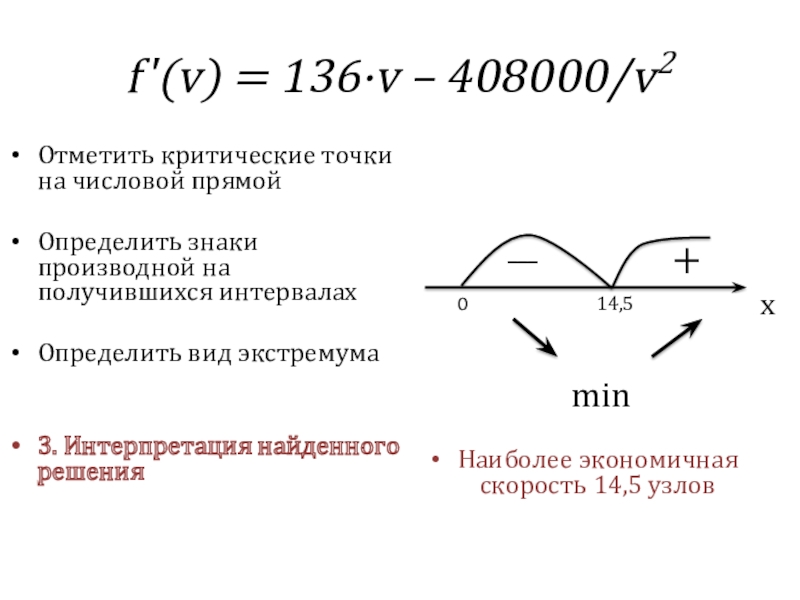
Слайд 35f'(v) = 136·v – 408000/v2
Отметить критические точки на числовой прямой
Определить знаки
производной на получившихся интервалах
Определить вид экстремума
3. Интерпретация найденного решения
Определить вид экстремума
3. Интерпретация найденного решения
Наиболее экономичная скорость 14,5 узлов
0
14,5
___
+
х
min
Слайд 36Определим дополнительную прибыль за рейс
f(v) = k·v2 + b/v
Рейс:
Архангельск – Нарьян – Мар ,
расстояние 1250 км.
Переведем 1250 км в мили:
1 миля = 1852 м,
1250 км = 1250000/1852 =
674,95 миль
При скорости 10 узлов время рейса -
t1 = 674.95/10 =67,95 час
При скорости 14,5 узлов время рейса –
t2 = 674.95/14,5 =46,55 час
расстояние 1250 км.
Переведем 1250 км в мили:
1 миля = 1852 м,
1250 км = 1250000/1852 =
674,95 миль
При скорости 10 узлов время рейса -
t1 = 674.95/10 =67,95 час
При скорости 14,5 узлов время рейса –
t2 = 674.95/14,5 =46,55 час
Слайд 37b = 408 000 руб. , k = 68
При скорости 10
узлов
f(10) = 68·102 + 408000/10 = 6800 +40800 =
47600 руб. в час
Стоимость рейса
S1 = 47600·67.95 = 3 234 420 руб.
При скорости 14,5 узлов
f(14,5) = 68·14,52 + 408000/14,5 = 14297 +28137,9 = 42434,9 руб. в час
Стоимость рейса
S2 = 42434,9 ·46,55= 1 975 344,6 руб.
f(10) = 68·102 + 408000/10 = 6800 +40800 =
47600 руб. в час
Стоимость рейса
S1 = 47600·67.95 = 3 234 420 руб.
При скорости 14,5 узлов
f(14,5) = 68·14,52 + 408000/14,5 = 14297 +28137,9 = 42434,9 руб. в час
Стоимость рейса
S2 = 42434,9 ·46,55= 1 975 344,6 руб.
Определим дополнительную прибыль за рейс
f(v) = k·v2 + b/v
Слайд 38Дополнительная прибыль
S1 - S2 = 3 234 420 - 1 975
344,6 =
= 1 259 075,4 руб.
= 1 259 075,4 руб.
Определим дополнительную прибыль за рейс
f(v) = k·v2 + b/v
Слайд 39Домашнее задание
1.Теплоход движется по прямой согласно закону
, где S(t) путь в милях и t – время в часах. В какой момент времени скорость теплохода будет наибольшей и какова величина этой скорости, если движение рассматривать за промежуток времени от
до ?
до ?
Слайд 40Надо ли знать формулы для вычисления
производных функций?
В чем
заключается механический смысл производной?
Как называется производная расстояния по времени?
Как найти ускорение, зная скорость?
Как называется производная расстояния по времени?
Как найти ускорение, зная скорость?
Нужно ли, по Вашему мнению, изучать тему «Производная» с точки зрения подготовки к профессии?
Почему?
Довольны ли Вы своей оценкой успеваемости за урок?
