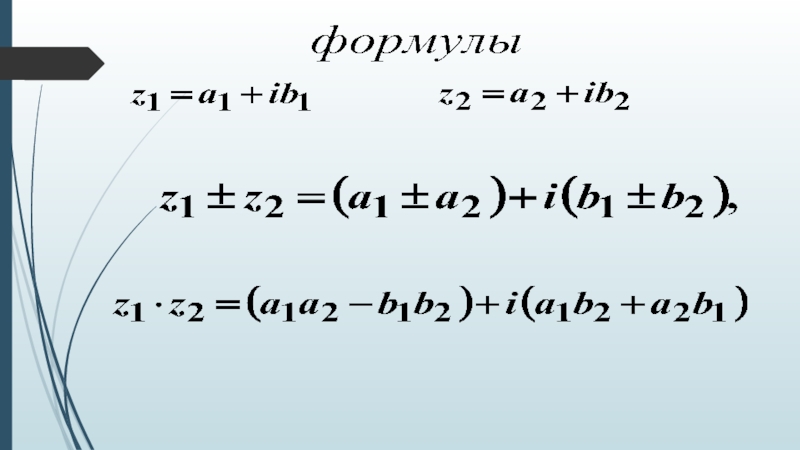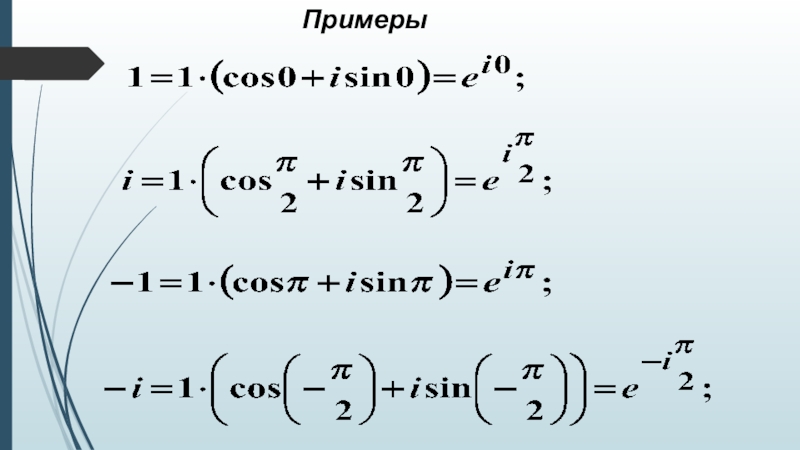Преподаватель математики
Осипова Галина Владимировна
г. Калининград
2018г.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по теме Комплексные числа
Содержание
- 1. Презентация к уроку по теме Комплексные числа
- 2. Цели урока
- 3. Слайд 3
- 4. Комплексное числоb – мнимая часть – Im
- 5. История открытияВ XVI веке возникла потребность в
- 6. Классификация чиселКомплексные числаa + biДействительные числа
- 7. Степени мнимой единицы
- 8. Действия с комплексными числами, записанными в алгебраической формеСравнениеСложение (вычитание)УмножениеДелениеВозведение в степень
- 9. комплексно сопряженные числа
- 10. Слайд 10
- 11. Деление
- 12. Примеры
- 13. Найти ошибку (-3 + 5i) + (4 – 8i) = 7 +13i(1-2i)-(2-i)=1-I(5+i)+(2-i)=3+2i
- 14. Проверь себя
- 15. Геометрическое изображение комплексных чиселВсякое комплексное число
- 16. Слайд 16
- 17. Тригонометрическая форма записи комплексных чиселОбозначим через r
- 18. Модуль и аргумент комплексного числаПолярные координатыМодуль комплексного числа: Аргумент комплексного числа: Главное значение аргумента.
- 19. Тригонометрическая форма записиформула Эйлера: Показательная форма записи
- 20. Формула Муавра
- 21. Примеры
- 22. Области применения комплексных чисел: Электротехника
- 23. Квантовая механика
- 24. АвиацияКомплексные числа широко использовал отец русской авиации
- 25. Число i позволяет свести в одной формуле
- 26. Слайд 26
- 27. Слайд 27
- 28. использованные ресурсы Андронов И.К.
- 29. Урок математики тема: Комплексные числа
Цели урока - Расширить представление о числах - Обобщить и систематизировать понятие комплексных чисел
Слайд 1ГАУ КО «Колледж Предпринимательства» Презентация урока математики Комплексные числа.
Слайд 2Цели урока
- Расширить представление о числах
- Обобщить и систематизировать понятие комплексных чисел
- Сформировать навыки действий с комплексными числами
-Воспитывать культуру общения, умение говорить и
аргументировать свою речь.
-Способствовать развитию мыслительных операций таких как
анализ, обобщение, логическое мышление; развивать
творческие способности.
- Обобщить и систематизировать понятие комплексных чисел
- Сформировать навыки действий с комплексными числами
-Воспитывать культуру общения, умение говорить и
аргументировать свою речь.
-Способствовать развитию мыслительных операций таких как
анализ, обобщение, логическое мышление; развивать
творческие способности.
Слайд 5История открытия
В XVI веке возникла потребность в извлечении квадратного корня из
отрицательного числа
Открытие принадлежало итальянскому математику Джероламо Кардано в 1545году.
Числа новой породы Кардано назвал «чисто отрицательными» или «софистически отрицательными»
Открытие принадлежало итальянскому математику Джероламо Кардано в 1545году.
Числа новой породы Кардано назвал «чисто отрицательными» или «софистически отрицательными»
1501-1576 гг.
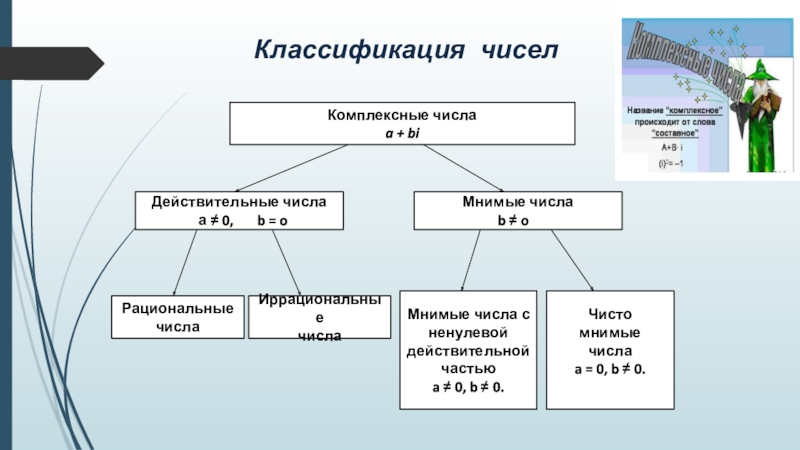
Слайд 6Классификация чисел
Комплексные числа
a + bi
Действительные числа
а ≠ 0, b = o
Мнимые числа
b ≠ o
Рациональные
числа
Иррациональные
числа
Мнимые числа с
ненулевой
действительной
частью
a ≠ 0, b ≠ 0.
Чисто
мнимые
числа
a = 0, b ≠ 0.
Слайд 8Действия с комплексными числами, записанными в алгебраической форме
Сравнение
Сложение (вычитание)
Умножение
Деление
Возведение в степень
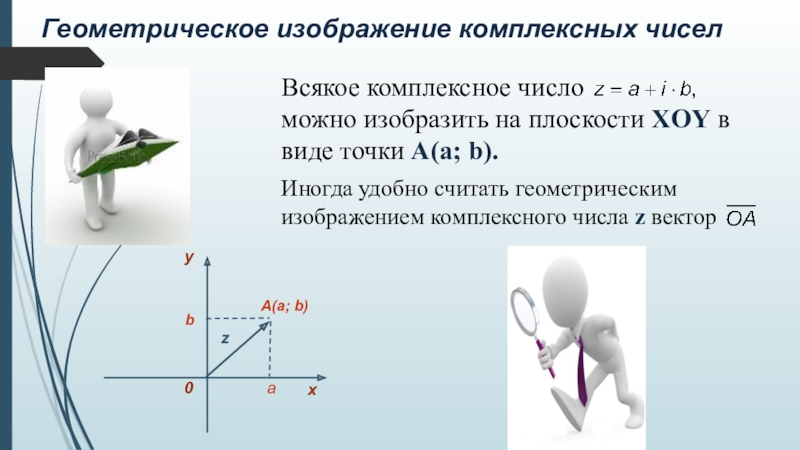
Слайд 15Геометрическое изображение комплексных чисел
Всякое комплексное число
можно изобразить на плоскости XOY в виде точки A(a; b).
Иногда удобно считать геометрическим изображением комплексного числа z вектор
Иногда удобно считать геометрическим изображением комплексного числа z вектор
a
A(a; b)
b
z
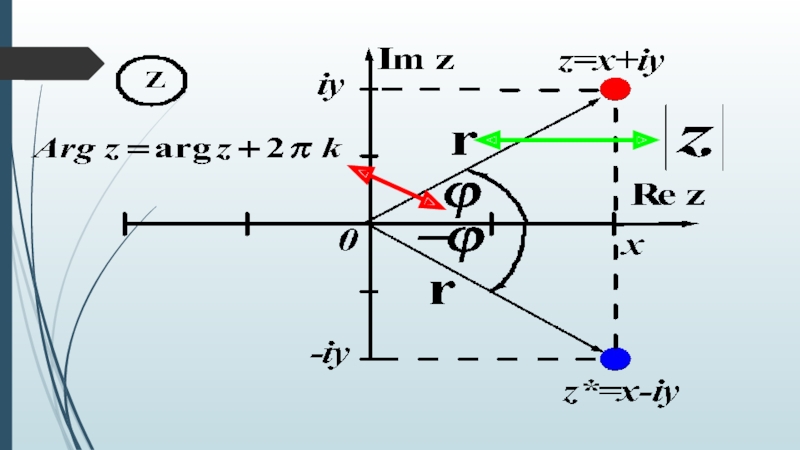
Слайд 17Тригонометрическая форма записи комплексных чисел
Обозначим через r модуль вектора
, через φ угол между вектором
и положительным направлением оси OX.
Тогда имеют место равенства:
Следовательно, комплексное число z
можно представить в виде:
и положительным направлением оси OX.
Тогда имеют место равенства:
Следовательно, комплексное число z
можно представить в виде:
φ
r
Слайд 18Модуль и аргумент комплексного числа
Полярные координаты
Модуль комплексного числа:
Аргумент комплексного числа:
Главное значение аргумента.
Слайд 24Авиация
Комплексные числа широко использовал отец русской авиации Н. Е. Жуковский (1847
– 1921) при разработке теории крыла, автором которой он является.
Слайд 25Число i позволяет свести в одной формуле главные математические константы и
действия.
Формула
Некоторые говорят, что эта формула и такой сжатый свод правил математики можно отправлять инопланетянам, чтобы убедить их в нашей разумности.
Формула
Некоторые говорят, что эта формула и такой сжатый свод правил математики можно отправлять инопланетянам, чтобы убедить их в нашей разумности.
Слайд 28 использованные ресурсы
Андронов И.К. Математика действительных и комплексных чисел. – М.:
Просвещение, 2015.
Гордиенко Н.А., Беляева Э.С., Фирстов В.Е., Серебрякова И.В. Комплексные числа и их приложения: Учебное пособие. – Воронеж: ВГПУ, 2015.
Стройк Д.Я. «Краткий очерк истории математики». М., «Наука», 2016.
М.Я. Выгодский; Справочник по элементарной математике
http://ru.wikipedia.org – Википедия – свободная энциклопедия
http://www.nigma.ru – интеллектуальная поисковая система
Гордиенко Н.А., Беляева Э.С., Фирстов В.Е., Серебрякова И.В. Комплексные числа и их приложения: Учебное пособие. – Воронеж: ВГПУ, 2015.
Стройк Д.Я. «Краткий очерк истории математики». М., «Наука», 2016.
М.Я. Выгодский; Справочник по элементарной математике
http://ru.wikipedia.org – Википедия – свободная энциклопедия
http://www.nigma.ru – интеллектуальная поисковая система